Момент силы

Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки - полюса) и относительно оси.

Если имеется материальная точка О, к которой приложена сила , то момент силы относительно этой точки равен векторному произведению радиус-вектора , соединяющего точку О и точку приложения силы, на вектор силы :

.^{, (Н•м).}

М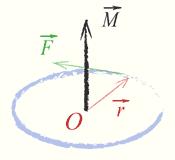 омент силы — аксиальный вектор⁴. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.4).

Рис. 4

Модуль момента силы:

M ₌ F_• l ₌ F _• r _• sin α,

где: M – момент силы (Ньютон^. метр),

F – приложенная сила,

r – расстояние от центра вращения до места приложения силы,

l = r^.sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,

α — угол, между вектором силы F и вектором положения r.

Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора М момента силы относительно любой точки О оси.

Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:

если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:

М₁ + М₂ + … + М_n = 0.

Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.5, силам F₁ и F₂ следует приписать положительный момент, а силе F₃ – отрицательный.

Рис. 5.

Момент импульса

Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).

Моментом импульса L материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r этой материальной точки, проведенного из точки О, на величину ее импульса p (рис. 6):

^(Дж•с),

где r – радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p – импульс частицы.

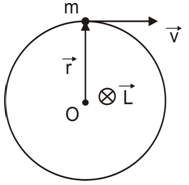
Рис.6.

Если твердое тело, вращающееся вокруг некоторой неподвижной оси z, представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела L_z относительно этой оси (L_z – скалярная величина).

Суммирование производим по всем элементарным массам m_i(имеющим линейную скорость v_i и радиус вращения r_i), на которые разбивается тело. Так как v_i=ωr_i, где ω - угловая скорость вращения тела, а I=∑m_ir_i² - момент инерции тела относительно данной оси, тогда момент импульса тела относительно оси z равен:

L_z = ∑ m_i v_i r_i = ∑ ω m_i r_i² = ω ∑ m_i r_i² = I_z ω .

В случае тела, вращающегося вокруг оси симметрии, векторы L и ω имеют одинаковое направление и тогда:

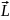= I . (1)

Продифференцируем выражение (1) по времени:

dL_z / dt = I_z dω / dt = I_z  = M_z,

В итоге:

L_z / dt = dM_z (2)

Таким образом, производная по времени от момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси:

dL / dt = M (3)

Из уравнения (3) видно, что если момент внешних сил, действующих на тело, равен нулю, то момент импульса тела остается постоянным.

Если M = 0, то: dL/dt = 0 ⇒ L = const. (4)

Выражение (4) представляет собой закон сохранения момента импульса:

момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно поворота замкнутой системы в пространстве на любой угол.