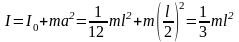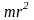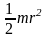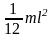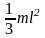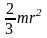- •Мурманский государственный технический университет, 2013
- •Введение …………………………………………………………………………...5 Лабораторная работа № 3. Изучение законов равноускоренного движения тел…………………………………………………………………………………..…20
- •Введение
- •Порядок выполнения лабораторных работ
- •Приборы для измерения линейных размеров тел
- •Миллиметровая линейка
- •Штангенциркуль
- •Как пользоваться штангенциркулем
- •Микрометр
- •Отсчет показаний
- •О погрешностях измерений
- •Порядок операций при обработке результатов серии измерений
- •При косвенных измерениях:
- •Лабораторная работа 3 Изучение законов равноускоренного движения тел
- •Приборы и материалы
- •Теоретические сведения
- •Основные понятия и законы Скорость
- •Ускорение
- •Ускорение точки при прямолинейном движении
- •Законы Ньютона
- •Первый закон Ньютона
- •Второй закон Ньютона
- •Третий закон Ньютона
- •.2. Теория лабораторной работы
- •У стройство и принцип действия прибора Атвуда
- •Следовательно, ускорение системы
- •Проверка формулы пути
- •Журнал наблюдений 1
- •Расчет погрешностей измерений:
- •2. Проверка формулы скорости
- •Журнал наблюдений 2
- •.3. Проверка второго закона Ньютона
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 5
- •Приборы и материалы
- •Теоретические сведения
- •Основные понятия и законы Кинематика вращательного движения
- •Равномерное вращательное движение
- •Неравномерное вращение
- •Равнопеременное вращение
- •Связь линейных и угловых характеристик
- •Момент инерции
- •Момент силы
- •Момент импульса
- •Основное уравнение динамики вращательного движения
- •Аналогия между поступательным и вращательным движениями
- •Теория лабораторной работы Устройство и принцип действия маятника Обербека
- •Измерения и обработка результатов
- •По формуле определить угловое ускорение 1, по формуле
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 6
- •Приборы и материалы
- •Теоретические сведения
- •Основные понятия и законы Свободное падение
- •Механические колебания
- •– По характеру взаимодействия с окружающей средой:
- •Гармонические колебания
- •Физический маятник
- •2. Теория лабораторной работы
- •Измерения и обработка результатов
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 8
- •Приборы и материалы
- •Теоретические сведения
- •1.Основные понятия и законы Гармонические колебания
- •Момент инерции
- •Момент силы
- •2. Теория лабораторной работы
- •И змерения и обработка результатов
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 12
- •Приборы и материалы
- •Теоретические сведения
- •Основные понятия и законы Деформация
- •Механическое напряжение
- •Закон Гука
- •Диаграмма растяжения
- •Кручение
- •2. Теория лабораторной работы Теоретические сведения
- •Описание установки
- •Измерения и обработка результатов
- •Литература
- •Лабораторная работа № 14
- •Приборы и материалы
- •Теоретические сведения
- •1.Основные понятия и законы Деформация
- •Закон Гука
- •Механическое напряжение
- •Диаграмма растяжения
- •2. Теория лабораторной работы Теоретические сведения
- •Измерения и обработка результатов
- •Журнал наблюдений
- •Окончательный результат:
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 15
- •Цель работы: Ознакомиться с явлением возникновения стоячих звуковых волн и определить опытным путем скорость звука в воздухе. Приборы и материалы
- •Теоретические сведения
- •Основные понятия и законы Упругие волны. Длина волны
- •Гармоническая волна
- •Бегущая волна
- •Интерференция волн
- •Стоячие волны
- •2. Теория лабораторной работы
- •Измерения и обработка результатов
- •Окончательный результат:
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 17 Определение момента инерции маховика
- •Приборы и материалы
- •Теоретические сведения .1. Основные понятия и законы Кинематика вращательного движения
- •Равномерное вращательное движение
- •Неравномерное вращение
- •Равнопеременное вращение
- •Связь линейных и угловых характеристик
- •Момент инерции
- •Момент силы
- •Момент импульса
- •Основное уравнение динамики вращательного движения
- •.2. Теория лабораторной работы Теоретические сведения
- •Описание установки
- •Измерения и обработка результатов
- •Расчет погрешностей измерений:
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 19
- •Приборы и материалы
- •Теоретические сведения
- •.2. Теория лабораторной работы
- •Описание установки
- •Измерения и обработка результатов
- •Определение коэффициента теплопроводности твердого тела
- •Теоретические сведения .1. Основные понятия и законы Явления переноса
- •Теплопроводность в твердых телах
- •Уравнение теплопроводности
- •Теория лабораторной работы Теоретические сведения
- •О писание установки
- •Измерение и обработка результатов
- •Контрольные вопросы:
- •Литература
- •Лабораторная работа 21 Определение отношения теплоемкостей газа
- •Цель работы: Найти величину отношения cp /cv для воздуха. Приборы и материалы
- •Теоретические сведения .1. Основные понятия и законы Теплоёмкость
- •Удельная и молярная теплоёмкости
- •Адиабатный процесс
- •.2. Теория лабораторной работы
- •Измерения и обработка результатов
- •Окончательный результат:
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 22
- •Приборы и материалы
- •Теоретические сведения .1. Основные понятия и законы
- •1.1 Строение жидкости
- •1.2 Поверхностное натяжение
- •1.3. Коэффициент поверхностного натяжения
- •1.4. Определение коэффициента поверхностного натяжения
- •.2. Теория лабораторной работы Теоретические сведения
- •Измерения и обработка результатов
- •Расчет погрешностей измерений:
- •Контрольные вопросы
- •Литература
- •Лабораторная работа 24 Определение коэффициента вязкости жидкости по методу Стокса
- •Приборы и материалы
- •Теоретические сведения /1.Основные понятия и законы Явление внутреннего трения (вязкость)
- •Влияние температуры на вязкость
- •Сила вязкого трения
- •Вязкость газов
- •.2. Теория лабораторной работы Теоретические сведения
- •О писание установки
- •Измерения и обработка результатов
- •Журнал наблюдений
- •Литература
- •Лабораторная работа 25 Изменение энтропии при нагревании и плавлении олова
- •Приборы и материалы
- •Теоретические сведения
- •1.Основные понятия и законы Термодинамическая фаза. Фазовый переход
- •Плавление твердых тел
- •Обратимые и необратимые процессы
- •Второй закон термодинамики
- •Энтропия
- •Термодинамический подход
- •Закон возрастания энтропии
- •Статистический подход
- •Второе начало термодинамики и «тепловая смерть Вселенной»
- •Измерение энтропии
- •2.Теория лабораторной работы Теоретические сведения
- •Измерения и обработка результатов
- •Журнал наблюдений
- •Контрольные вопросы
- •Литература
Равномерное вращательное движение
Если угловая скорость ω = const, то вращательное движение называется равномерным.
При равномерном вращении его быстроту также описывают частотой оборотов n и периодом вращения T.
Частота оборотов n равна числу оборотов, сделанных за единицу времени,
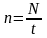
Где N – число оборотов за время t.
Т.к. за один оборот тело поворачивается на угол, равный 2, то
= 2N и = 2n
Период вращения T – это время, за которое тело совершает один оборот.
Т.к.
 ,
то
,
то
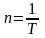 ,
.
,
.
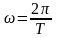
[ω]= рад/с , [n]= об/с , [T]= с
Уравнение равномерного вращения имеет вид
φ = φ0 + ωt.
В частном случае, когда начальный угол поворота
φ0 = 0, φ = ωt.
Угловую скорость равномерно вращающегося тела
ω = φ / t
можно выразить и так: ω = 2π / T,
где: T – период вращения тела;
φ = 2π – угол поворота за один период.
Неравномерное вращение
Неравномерное вращение (угловая скорость изменяется со временем) характеризуется угловым ускорением .
Угловое
ускорение
![]() 3
-
вектор, равный производной от угловой
скорости
по
времени t
,
3
-
вектор, равный производной от угловой
скорости
по
времени t
,
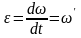 ,
,
dω - изменение угловой скорости за время dt.
[
]=
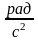
Векторы
 и
направлены
по оси вращения тела. При ускоренном
вращении тела
направления векторов
и
направлены
по оси вращения тела. При ускоренном
вращении тела
направления векторов
![]() и
и
![]() совпадают,
при замедленном – противоположны (рис.
2).
совпадают,
при замедленном – противоположны (рис.
2).
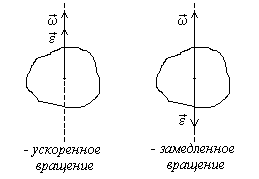
Рис. 2
Равнопеременное вращение
Если угловое ускорение ε = const, то вращательное движение называется равнопеременным. Равнопеременное вращение характеризуется следующими уравнениями:
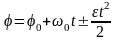 и
= 0
+ t,
и
= 0
+ t,
0 и 0 – угловая скорость и угол поворота тела в начальный момент t0=0,
и – в момент времени t. При ускоренном вращении в этих уравнениях выбирается знак «+», а при замедленном – знак «–».
Связь линейных и угловых характеристик
Если точка тела отстоит от оси вращения на расстоянии r, то за время dt она проходит путь
dS = dr
Скорость точки
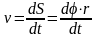 ,
или v
=
r
,
или v
=
r
При вращении тела тангенциальное ускорение его точки
 ,
или
,
или
a=r
Нормальное ускорение точки тела
 ,
или
,
или
/an= 2r
Полное ускорение, как указывалось ранее, определяют по формуле
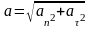
Момент инерции
Момент инерции - скалярная величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Единица измерения СИ: кг·м². Обозначение: I или J.
Момент инерции тела относительно оси вращения зависит от массы тела и от распределения этой массы относительно этой оси. Чем больше масса тела и чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело.
Момент инерции элементарной (точечной) массы mi, отстоящей от оси на расстоянии ri, равен:
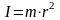
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
![]() ,
,
где:
mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
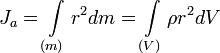 ,
,
где:
![]() —
масса
малого элемента объёма тела
—
масса
малого элемента объёма тела
![]() ,
,
![]() —
плотность,
—
плотность,
![]() —
расстояние
от элемента
до
оси a.
—
расстояние
от элемента
до
оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
![]()
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения |
|||
Тело |
Описание |
Положение оси a |
Момент инерции Ja |
|
Материальная точка массы m |
На расстоянии r от точки, неподвижная |
|
|
Полый тонкостенный цилиндр или кольцо радиуса r и массы m |
Ось цилиндра |
|
|
Сплошной цилиндр или диск радиуса r и массы m |
Ось цилиндра |
|
|
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 |
Ось цилиндра |
|
|
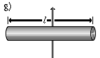
Прямой тонкий стержень длины l и массы m |
Ось перпендикулярна к стержню и проходит через его центр масс |
|
|
Прямой тонкий стержень длины l и массы m |
Ось перпендикулярна к стержню и проходит через его конец |
|
|
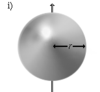
Тонкостенная сфера радиуса r и массы m |
Ось проходит через центр сферы |
|
|
Шар радиуса r и массы m |
Ось проходит через центр шара |
|
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния а между осями:
J = Jc + ma2.
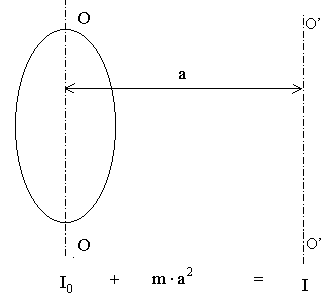
Рис. 3
где
![]() —
полная масса тела (рис. 3).
—
полная масса тела (рис. 3).
Например, момент инерции стержня относительно оси, проходящей через его конец, равен: