Лабораторная работа № 9 определение скорости полета ружейной пули

ТБ: Перед началом работы изучите методические указания по ТБ в лабораторной работе № 9.

1.Внимательно изучите порядок выполнения работы.

2.При работе с пневматическим ружьем будьте внимательны при выстреле, некто не должен стоять рядом с установкой.

3.При неисправности установки сообщите лаборанту или преподавателю.

Цель работы: Определить экспериментально скорость полета пули пневматического ружья двумя способами - кинематическим и динамическим.

Кинематический способ

Этот способ основан на измерении времени, в течении которого пуля пролетает известное расстояние между двумя дисками. Пусть эти два диска, которое находится на расстоянии d друг от друга, вращаются с угловой скоростью . Предположим, что за время пролета t пули между двумя вращающимся дисками, они поворачиваются на угол (см. рис.1).

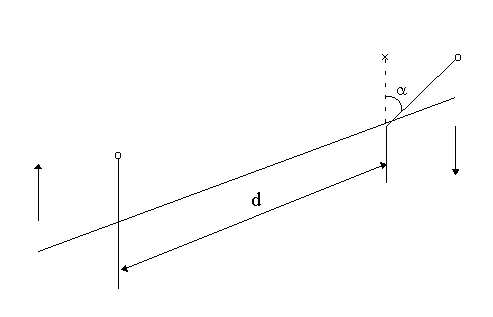
Рис.1

Тогда время пролета t можно определить по формуле:

(1)

либо выразить следующим образом:

, (2)

где - модуль скорости пули.

Приравняв правые части формул (1) и (2) находим выражение для модуля скорости пули:

(3)

Используя связь модуля угловой скорости с числом оборотов n дисков в секунду формулу (3) можно переписать в виде:

(4)

в которой следует измерять в радианах. Однако удобнее угол .измерять в градусах. При этом модуль угловой скорости должен измеряться в град/сек. Окончательно запишем:

(5)

Динамический способ

В этом способе скорость пули определяется с помощью баллистического маятника. Баллистический маятник представляет собой цилиндр, который заполнен пластилином и подвешен в горизонтальном положении на длинных и тонких нитях. Летящая свинцовая пуля входит в пластилин и сообщает маятнику некоторую скорость, в результате чего маятник отклоняется на определенный, угол который может быть измерен.

Определение скорости полета пули основано на применении законов сохранения количества движения и механической энергии системы. Удар пули о пластилин можно считать абсолютно неупругим. При таком предположении запишем закон сохранения количества движения в следующем виде:

(6)

где m - масса пули, - модуль ее скорости до удара, M - масса маятника, ₁ - модуль скорости центра масс пули и маятника сразу после удара. Так как масса пули мала по сравнению с массой маятника, то ею можно пренебречь, переписав (6) в виде:

(7)

Модуль скорости маятника с пулей ₁ можно определить из закона сохранения полной механической энергии. В момент удара пули о маятник их кинетическая энергия равна:

. (8)

Центр масс маятника с пулей отклоняется от положения равновесия, поднимаясь в крайнем положении на высоту h от первоначального положения (рис. 2). При этом изменение потенциальной энергии системы пули - маятник равно их начальной кинетической энергии:

(9)

Отсюда

(10)

и равенство (7) запишется в виде:

(11)

Поскольку непосредственное измерение h затруднительно, то удобно выразить ее через длину маятника l (расстояние от точки подвеса до центра масс маятника) и угол его отклонения от положения равновесия (см. рис. 2). Из треугольника АВС имеем: . Отсюда:

. (12)

Подставляя (12) в (11) получаем для модуля скорости пули:

(13)

При малых углах синус можно заменить значением аргумента. Тогда

. (14)

Здесь угол измеряется в градусах.