
Кириллов Прикладные методы оптимизации / Лабораторная работа №4 по ПМО
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра экономической информатики
Лабораторная работа №4
по дисциплине
«Прикладные методы оптимизации»
на тему «Динамическое
программирование»
Выполнили
Группа: ФБИ – 22.
Преподаватель: Кириллов Ю.В.
Новосибирск 2014
-
Цель работы:
-
Приобретение навыков решения задачи динамического программирования о достижении цели в среде ПЭР.
-
Приобретение навыков решения задачи динамического программирования управления запасами в среде ПЭР.
-
Условие задачи о выборе оптимальной траектории самолета.
Условие задачи достижения цели:
Самолет, находящийся
на высоте
 и имеющий скорость
и имеющий скорость
 ,
должен подняться на высоту
,
должен подняться на высоту
 и набрать скорость
и набрать скорость
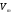 .
Известен расход горючего при подъеме
самолета на любую высоту
.
Известен расход горючего при подъеме
самолета на любую высоту
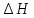 при постоянной скорости, а также
увеличении скорости на любую величину
при постоянной скорости, а также
увеличении скорости на любую величину
 при неизменной высоте. Требуется найти
оптимальный вариант управления набором
высоты и скорости, при котором общий
расход горючего будет минимальным.
Необходимые данные задать самостоятельно.
при неизменной высоте. Требуется найти
оптимальный вариант управления набором
высоты и скорости, при котором общий
расход горючего будет минимальным.
Необходимые данные задать самостоятельно.
Пусть
координаты начальной точки
 ,
а конечной точки
,
а конечной точки
 .
Длины каждого отрезка координатной
сетки по горизонтали и вертикали
составят:
.
Длины каждого отрезка координатной
сетки по горизонтали и вертикали
составят:
|
∆V |
∆H |
|
12 |
5 |
-
Результаты расчетов по шагам динамического процесса и оптимальное решение.
Результаты расчетов по шагам динамического процесса приведены на рисунках 1-2.

Рисунок 1 – Шаги для состояний 4,5

Рисунок 2 – Шаги для состояний 1,2,3
Итоговое решение задачи с помощью ПЭР представлено на рисунке 3.

Рисунок 3 – Итоговое решение задачи с помощью ПЭР
Можно построить оптимальную траекторию перемещения самолета из точки A в точку B, заданных по условию задачи (рисунок 4).

Рисунок 4 – Оптимальная траектория перемещения самолета
-
Исходные данные для задачи управления запасами.
Условие задачи управления запасами:
Предприятие
производит продукцию, спрос на которую
в каждом из 4-х месяцев известен и
составляет
 единиц готовой продукции. Запас готовой
продукции на складе предприятия на
начало планируемого периода равен
единиц готовой продукции. Запас готовой
продукции на складе предприятия на
начало планируемого периода равен
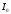 единиц. В начале каждого месяца, в котором
выпускается продукция, требуется
переналадка оборудования, затраты на
которую равны
единиц. В начале каждого месяца, в котором
выпускается продукция, требуется
переналадка оборудования, затраты на
которую равны
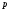 ден. единиц. Затраты на производство
единицы продукции равны
ден. единиц. Затраты на производство
единицы продукции равны
 ден. единиц, а затраты на ее хранение -
ден. единиц, а затраты на ее хранение -
 ден. единиц.
ден. единиц.
Складские
площади и производственные мощности
предприятия ограничены, поэтому хранить
на складе можно не более
 ,
а производить в месяц не более
,
а производить в месяц не более
 единиц готовой продукции. При этом запас
продукции на складе к концу планируемого
периода должен быть равен нулю.
единиц готовой продукции. При этом запас
продукции на складе к концу планируемого
периода должен быть равен нулю.
Требуется
определить такой план выпуска продукции
 в каждом месяце, который удовлетворил
бы текущий спрос и обеспечил бы общие
минимальные затраты на производство и
хранение продукции за весь планируемый
период.
в каждом месяце, который удовлетворил
бы текущий спрос и обеспечил бы общие
минимальные затраты на производство и
хранение продукции за весь планируемый
период.
Числовые данные варианта №4:
|
№ |
I0 |
B |
M |
c |
h |
p |
s1 |
s2 |
s3 |
s4 |
|
4 |
4 |
6 |
5 |
6 |
3 |
8 |
5 |
6 |
5 |
4 |
-
Результаты расчетов по шагам динамического процесса и оптимальное решение.
Условно-оптимальные варианты управления для каждого состояния системы, выведенные при решении задачи в среде ПЭР по обратной схеме, последовательно представлены на рисунках 5-8.

Рисунок 5 – Период 4

Рисунок 6 – Период 3
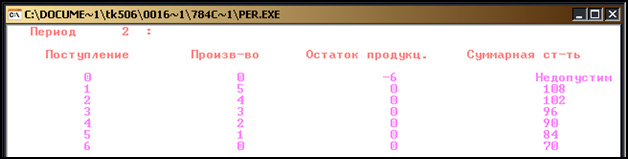
Рисунок 7 – Период 2

Рисунок 8 – Период 1
Итоговое решение задачи с помощью ПЭР показано на рисунке 9.

Рисунок 9 – Итоговое решение задачи в среде ПЭР
-
Анализ полученного решения.
Таким образом, оптимальный план производства готовой продукции

и ее хранения
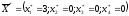
позволяет наилучшим образом построить процесс управления производством в данной задаче, потому что затраты в этом случае будут наименьшими и составят

-
Выводы по работе.
В результате выполнения работы были получены навыки решения задач динамического программирования в среде ПЭР, в частности о достижении цели и управления запасами.
