Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Новосибирский государственный технический университет»

Кафедра экономической информатики

Расчетно-графическая работа №1

По курсу «Исследование операций»

«Линейное программирование»

Студент группы ФБИ-22

Преподаватель: к.т.н., доцент кафедры ЭИ

Кириллов Ю. В.

Новосибирск, 2014

Цели задания:

1. Понимать смысл, различать, осознанно использовать следующие понятия:

математическая модель задачи линейного программирования (ЗЛП);

• формы записи ЗЛП;

• геометрическая интерпретация ЗЛП;

• линии уровня функции;

• градиент функции;

• двойственные задачи;

• двойственные оценки;

• устойчивость решения ЗЛП;

• устойчивость оценок.

2. получить навыки, уметь:

• строить математические модели ЗЛП;

• переходить от одной формы записи ЗЛП к другой;

• решать графически ЗЛП с двумя переменными;

• строить модель задачи, двойственной к исходной;

• находить решение ЗЛП на основе решения задачи, двойственной к ней;

• интерпретировать полученные результаты в терминах решаемой задачи;

• проводить анализ устойчивости решения ЗЛП на основе геометрической интерпретации.

Ход работы:

1. Записали математическую модель задачи.

2. Построили модель задачи, двойственной к заданной, и дала ее геометрическую интерпретацию.

3. Решили двойственную задачу графически. Используя полученный результат, нашли

решение исходной задачи.

4. Дали экономическую интерпретацию двойственным оценкам.

5. Произвели анализ устойчивости полученного решения и двойственных оценок на основе геометрической интерпретации двойственной задачи.

6. Решили задачу с помощью Пакета Экономических расчетов (ПЭР) и сравнили результаты решения с результатами, полученными вручную.

7. Решили задачу с помощью электронных таблиц Microsoft Excel и сравнили результаты с результатами, полученными ранее.

Условие задачи : Коммерческая фирма предполагает осуществить оптовую закупку продовольствия, располагая для этого суммой S рублей. Номенклатура продовольствия включает пять наименований. Покупная цена каждого вида продукта равна соответственно s1, s2, s3, s4 и s5 рублей за килограмм. В распоряжении фирмы имеются холодильные камеры общей площадью V кв. метров. Площадь, необходимая для хранения одного килограмма продукта каждого вида, равна соответственно v1, v2, v3, v4 кв. м; при этом продукт пятого вида хранению не подлежит и должен быть реализован 4 немедленно. При своевременной реализации продукта каждого вида прибыль фирмы составит соответственно p1, p2, p3, p4 и p5 рублей за килограмм.

Определить объемы закупки продовольствия каждого вида, при которых фирма может рассчитывать на максимальную прибыль.

Вариант задания:

Таблица 1. Вариант задания

Решение задачи:

Составим математическую модель для данной задачи. Для этого примем количество закупаемого первого товара за x1, второго за x2, третьего за x3, четвертого за x4, пятого за x5.

Целевая функция – это функция, показывающее какое количество прибыли будет получено фирмой от реализации продукции. В нашем случае – от продуктов x1, x2,x3,x4,x5 соответственно.

Поскольку в данной задаче цель фирмы получить максимально возможную прибыль, то целевая функция должна стремится к максимуму. Другими словами: наша цель – максимизация прибыли, а, следовательно, и максимизация целевой функции.

В общем виде функция имеет вид:

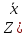)=p₁*x₁+p₂*x₂+p₃*x₃+p₄*x₄+p₅*x₅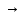max

Однако, поскольку действия фирмы ограничены запасами имеющихся ресурсов, то для достижения поставленных целей необходимо рационально их использовать.

Необходимо составить ограничения:

• для запасов денег, выделенных для закупки необходимых объемов продукции;

• для площадей холодильников, отведенных под хранение продуктов.

Поскольку последний продукт x5 не подлежит хранению, то во второе условие он включен не будет.

В общем случае условия можно представить в виде:

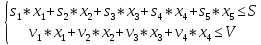
Стоит заметить, что все переменные должны удовлетворять условию:

Таким образом, задача сводится к набору условий.

Z(x)=18x₁+20x₂+48x₃+5x₄+12x₅→max

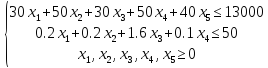
Обратимся к построению задачи двойственной к данной.

Поскольку модель исходной задачи имеет лишь 2 ограничения, то модель двойственной задачи будет содержать только две переменные.

Примем в качестве переменных y1 – затраты по первому виду ресурсов и y2 – затраты по второму виду ресурсов.

Поскольку цель фирмы минимизировать свои затраты, то функция будет стремиться к минимизации.

В общем виде модель двойственной задачи имеет вид:

)=S*y₁+V*y₂min

Что касается ограничений двойственной задачи, то их количество равно числу переменных прямой задачи.

В общем виде ограничения двойственной задачи можно записать в виде системы:

Необходимо учесть, что переменные должны быть неотрицательными:

Модель двойственной задачи:

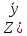)=7000*y₁+120*y₂min

Графическое решение двойственной задачи:

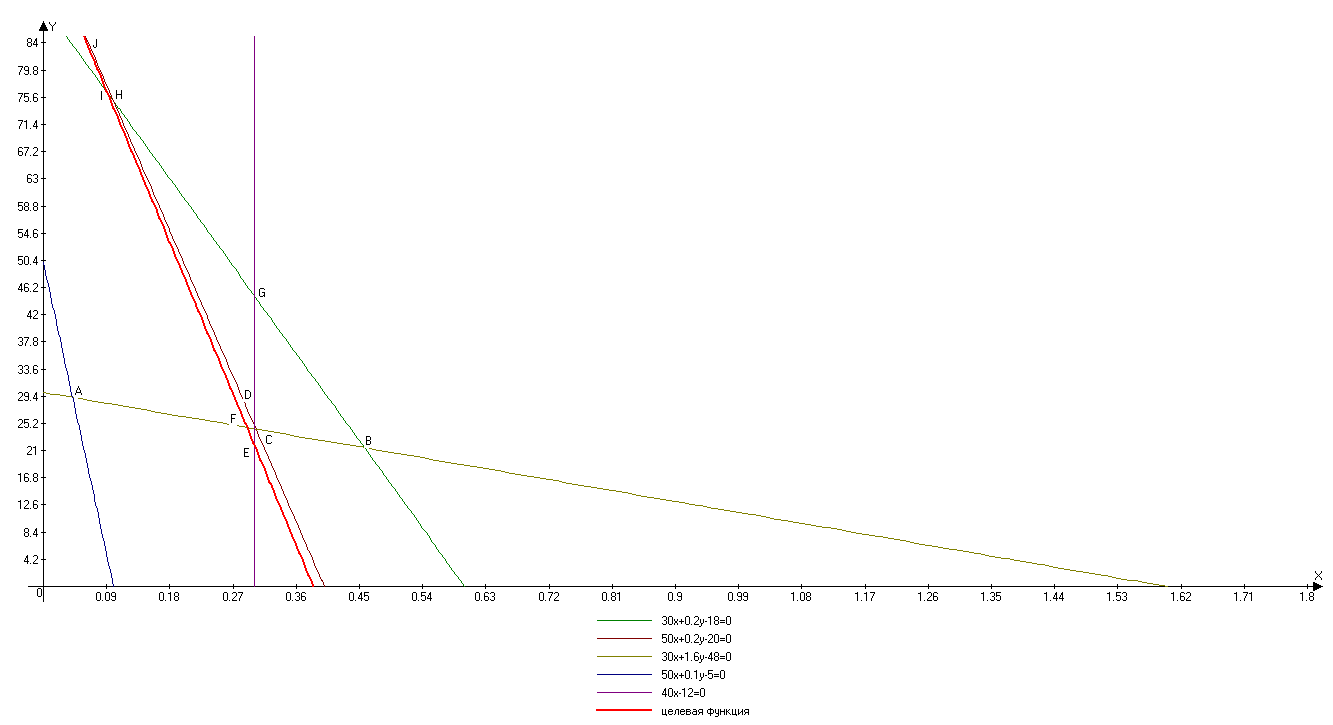
Рисунок 1. Графическое решение двойственной задачи

Можно заметить из графика, что в данном решении существует 10 угловых точек (A,B,C,D,E,F,G,H,I,J). Определить оптимальную точку можно двумя способами:

• подстановка координат точек пересечения в целевую функцию;

• нахождение градиента целевой функции.

Воспользуемся вторым способом.

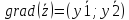
Для исследуемой функции градиент равен:

Представим в более удобном виде(учитывая масштаб графика).

)

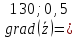К градиенту построим линию нормали. Перемещая линию нормали вдоль линии градиента, получим, что оптимум находится в точке B.

Найдем координаты этой точки.

y2=30 y1=

Таким образом, получаем, что:

y1=0.2 – это оценка относительной стоимости каждого вида продукта;

y2=30 – это оценка относительной стоимости площадей, необходимых для хранения одного килограмма продукта каждого вида.

Найдем значение целевой функции:

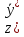)=7000*0.2+120*30=1400+3600=5000

С помощью второй теоремы двойственности найдем решение прямой задачи.

Вторая теорема двойственности гласит: для того, чтобы планы прямой и двойственной задачи были оптимальны необходимо и достаточно выполнение следующих условий:

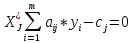
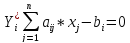
Т.е.



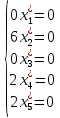
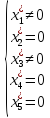
Таким образом, в оптимальном плане задачи только координаты x1 и x3 отличны от нуля. Составим соотношения по ограничениям задачи.

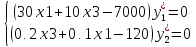
Так как

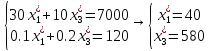
Найдем значение целевой функции:

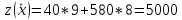
Итак, решение исходной задачи и значение целевой функции прямой и двойственной задачи равны друг другу и равны 5000.

Экономическая интерпретация:

Выпишем все переменные основной и двойственной задачи:

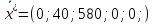
Пользуясь таблицей соответствия и конечной симплекс-таблицей выпишем все переменные двойственной задачи:

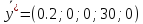
Величины показывают, что первого типа товара и третьего, нужно закупить в количестве 40 и 580 единиц. Товары второго, четвертого и пятого типов закупать нецелесообразно. Двойственные оценки это подтверждают. Двойственные оценки являются мерой убыточности производства и показывают разницу между себестоимостью товара и доходом, получаемым при его продаже.

Анализ устойчивости полученного решения и двойственных оценок:

Рисунок 2. Анализ устойчивости

b1=7000 b2=120

Очевидно, что при изменении количества ресурсов будет изменяться и общий доход, то есть целевая функция. Это подтверждается третьей теоремой двойственности.

Тогда:

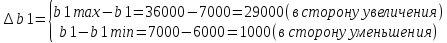
И

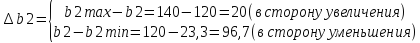
Таким образом, если запасы обоих ресурсов изменяются в указанных выше пределах, координаты оптимального плана двойственной задачи 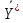= 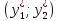не меняются, и новое значение целевой функции можно найти следующим образом:

Zнов=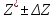

Где,

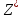- оптимальное значение, полученное из итоговой таблицы,

ΔZ – изменение целевой функции, найденное по формуле

При этом Δb1 и Δb2 – должны быть в пределах интервала устойчивости.

Представим уравнение линии уровня в следующей форме:

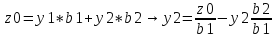
Где отношение 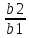показывает тангенс угла наклона прямой, соответствующей уравнению, к оси Oy1.

Линия уровня, проходящая через точку B имеет координаты , которые при изменении тангенса угла наклона линии уровня останутся неизменными, поэтому при изменении b1 прямая будет поворачиваться вокруг точки С, причем при увеличении b1 – по часовой стрелке, а при уменьшении и1 – соответственно против. Учитывая свойства параллельных прямых, найдем b1max(верхний предел устойчивости) и b1min(нижний предел устойчивости).

1. Поворот по часовой стрелки(при увеличении b1)

Рисунок 3. Графический анализ устойчивости двойственных оценок.

2. Поворот против часовой стрелки(при уменьшении b1)

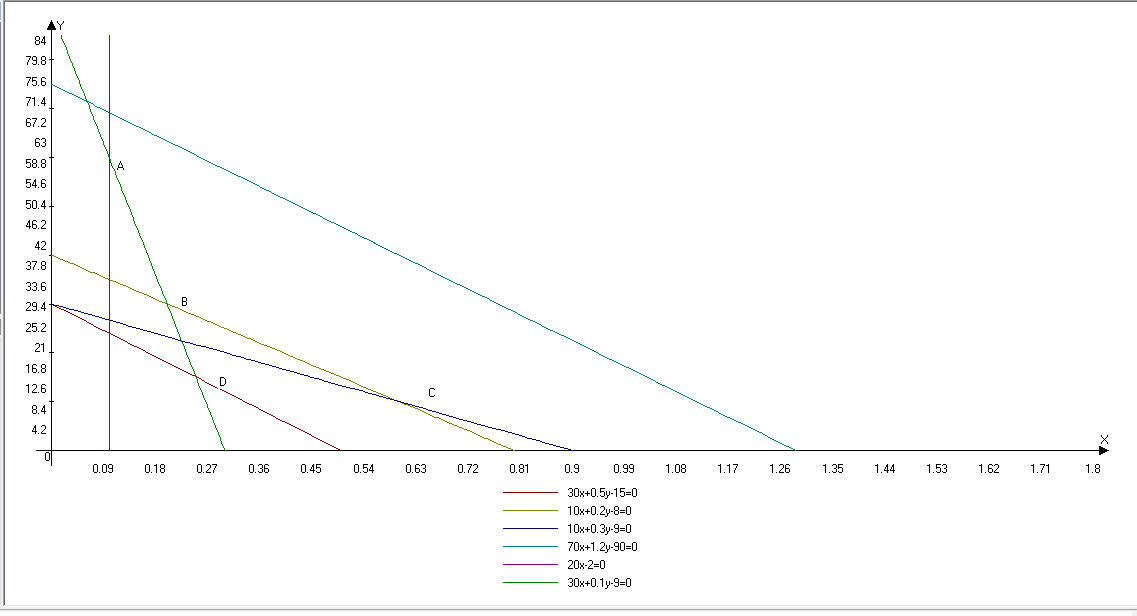
Рисунок 4. Графический анализ устойчивости двойственных оценок.

При уменьшении(увеличении) b1, а следовательно при повороте линии уровня против часовой стрелки оптимальная точка может изменяться и координаты 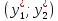изменятся.

При совпадении линии уровня

Zmax=y1*b1max+y2*120

И прямой

30y1+0,1y2=9

Имеем пропорцию:

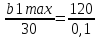
Получаем из пропорции b1max=36000, что полностью совпадает с решением полученным в ПЭР.

В случае, когда b1 уменьшается, при совпадении линии уровня и прямой 10y1+0.2y2=8

является выполнение соответствия:

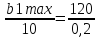
Тогда b1 min=6000, что также соответствует алгебраическому решению.

Пусть теперь изменяется b2, а b1 = const.

Очевидно, что эти изменения могут быть проиллюстрированы геометрически как для b1. Только наклон линии к оси Oy2. Тогда при увеличении b2, линия уровня будет поворачиваться вокруг B против часовой стрелки, пока не совпадет с прямой 30y1+0.1y2=9 , а это произойдет при условии:

Откуда b2max=23,3

Аналогично, уменьшение b2 приведет в конце концов к совпадению с прямой 10y1+0,2y2=8 при условии:

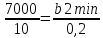
b2min=140. Как видно результаты полностью совпадают с решением найденным с помощью ПЭР.