1. Основы линейного программирования

1.1. Основные задачи линейного программирования и их формы. Математическое программирование (МП) – это раздел математики, посвященный теории и методам решения оптимизационных задач, т.е. задач об экстремумах функций нескольких переменных на множествах, заданных линейными и нелинейными ограничениями в виде равенств и неравенств. Задачи МП находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных способов действий, например, при решении проблем управления и планирования производственных процессов, в задачах проектирования и перспективного планирования. Наименование дисциплины обусловлено тем, что в МП решаются задачи нахождения оптимальной программы (плана) действий. В связи с этим МП является одним из центральных разделов в другой математической дисциплине – исследовании операций.

Задача МП формулируется следующим образом: найти значения переменных х₁^, х₂^, …, х_n^, при которых функция z(x₁,x₂,…,x_n) принимает максимальное (или минимальное) значение и, кроме того, на переменные наложены ограничения в виде равенств и неравенств.

Будем кратко записывать задачу в следующей форме:

z(x₁,x₂,…,x_n)max (min), (1)

g_i(x₁,x₂,…,x_n)0, i=1k, (2)

h_j(x₁,x₂,…,x_n)=0, j=1m. (3)

Функция z называется целевой функцией. В конкретных задачах могут отсутствовать ограничения-равенства, либо ограничения-неравенства. Может случиться, что на переменные вообще не накладываются никакие ограничения.

Набор чисел Х(х₁,x₂,…,x_n), удовлетворяющий ограничениям (2), (3), называется допустимым решением задачи (или допустимым планом). Все допустимые решения образуют область допустимых решений задачи (ОДР). Допустимое решение, при котором целевая функция достигает своего максимума (минимума), называется оптимальным решением (если оно существует).

В виде моделей МП могут быть представлены и решены задачи оптимизации из следующих областей:

1. планирование и организация производства;

2. оптимальное управление динамическими системами и процессами;

3. инженерный анализ и обработка больших потоков информации;

4. определение оптимальных маршрутов транспорта.

Этот список может быть значительно расширен. Приведём несколько примеров задач МП.

Задача 1 (задача оптимального планирования и организации производства). Для сборки двух приборов α и β применяют три типа микросхем А, В, С. На один прибор α затрачивается 3 микросхемы А и по 2 микросхемы В и С, а на один прибор β соответственно 2 микросхемы А, 4 микросхемы В и 3 микросхемы С. Запас микросхем А, В, С соответственно 27, 28 и 23 шт. Сколько приборов каждого вида необходимо собрать для получения максимального дохода, если стоимость одного прибора α 4 руб., а β – 20 руб.

■ Приведенные выше условия являются экономической постановкой задачи. Составим теперь математическую модель (постановку) задачи. Пусть х₁, х₂ – количество приборов α и β соответственно, планируемое к выпуску. Тогда суммарная стоимость всей плановой продукции (целевая функция) составит z=4x₁+7x₂max. При этом общий расход микросхем А равен 3x₁+2x₂, и он не должен превышать имеющегося запаса 27. Это приводит к ограничению 3x₁+2x₂27. Аналогично учитываются ограничения по микросхемам В и С: 2x₁+4x₂28, 2x₁+3x₂23. Т.к. объёмы выпускаемых изделий не могут быть отрицательны, то x₁0, x₂0. Т.о., математическая модель задачи имеет вид:

z=4x₁+7x₂max, (4)

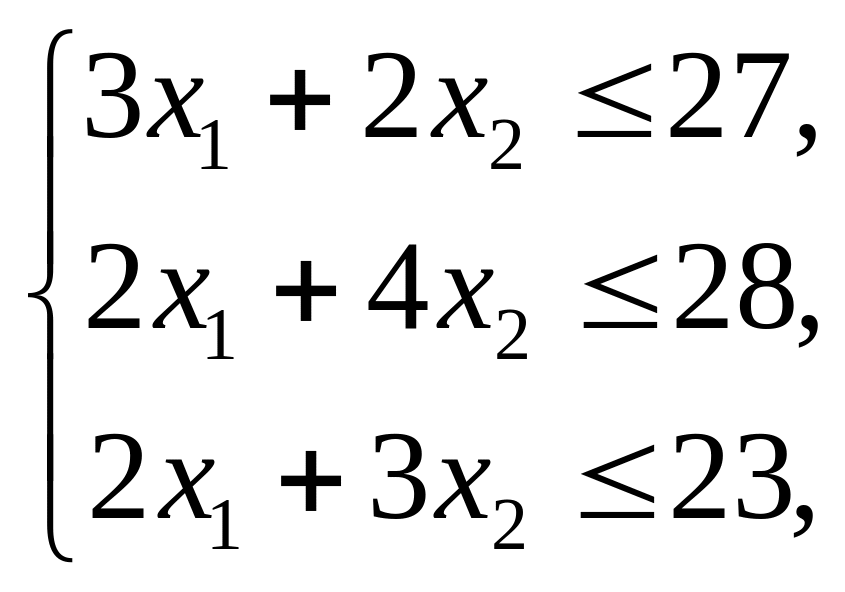(5)

x_i0, i=12. (6)

Таким образом, задача состоится в том, чтобы найти неотрицательные значения х_j, j=12, удовлетворяющие ограничениям (5), для которых функция z принимает наибольшее значение. ●

Задача 2 (транспортная задача (ТЗ) по критерию стоимости). Пусть некоторый однородный товар (кирпич, пиломатериалы и т.п.) хранится на m складах А_i (i=1m) и требуется в n пунктах В_j (j=1n). Известны следующие параметры: а_i – запас товара на i-м складе; b_j – потребность в товаре в j-м пункте; с_ij – стоимость перевозки единицы товара из i-го склада в j-й пункт. Предполагается, что стоимость перевозки произвольного количества товара пропорциональна этому количеству. Требуется составить план перевозок товара так, чтобы удовлетворить потребности при имеющихся запасах, обеспечив при этом наименьшую суммарную стоимость перевозок.

■ Приведённые выше условия – экономическая постановка задачи. Обозначим через х_ij количество товара, перевозимого из i-го склада в j-й пункт. Стоимость перевозки товара из А_i в В_j составит с_ijх_ij, а суммарная стоимость перевозок есть . Следовательно,

z= . (7)

Далее, все запасы из пункта А_i должны быть вывезены, т.е.

, i=1m. (8)

Все потребности пункта В_j должны быть удовлетворены, т.е.

, j=1n. (9)

Естественно предполагать также, что

х_ij0, i=1m, j=1n. (10)

Т.о., математическая модель ТЗ состоит в определении неотрицательного плана перевозок Х=(х_ij), для которого выполняются условия (8) и (9), а целевая функция (7) принимает наименьшее значение. Матрица Х=(х_ij)_m×n называется матрицей перевозок. ●

Если в задаче МП целевая функция, а также уравнения и неравенства системы ограничений линейны, то такая задача называется задачей линейного программирования (ЛП).

Различают три основные формы ЛП.

Стандартная форма – все ограничения являются ограничениями-неравенствами, а все переменные неотрицательны (удобна при решении задач ЛП графическим методом).

Каноническая форма – все ограничения являются ограничениями-равенствами с неотрицательными правыми частями, а все переменные неотрицательны. Основные вычислительные методы (симплекс-метод и его варианты) разработаны именно для этой формы.

Общая форма – часть ограничений являются равенствами, часть – неравенствами. Кроме того, не на все переменные наложены условия не отрицательности.

Эти три формы задачи ЛП эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных. Поэтому, если имеется способ решения одной из этих задач, тем самым мы умеем решать любую из трёх задач ЛП. Приведём следующую задачу ЛП, представленную в общей форме, к канонической форме:

z=3х₁+4х₂max,

2х₁+3х₂=12,

5х₁-6х₂≤7,

-3х₁+2х₂≤-4,