Итерация 0

БП	х1	х2	λ1	λ2	μ1	μ2	S1	S2	Реш.	Отн.
R1	2	0	2	1	-1	0	0	0	2	–
R2	0	6	-1	2	0	-1	0	0	3	1/2
S1	2	-1	0	0	0	0	1	0	6	–
S2	1	2	0	0	0	0	0	1	10	5
Оц.	-2	-6	-1	-3	1	1	0	0

Поскольку μ₂=0, вводимой в базис переменной может быть х₂, при этом из числа базисных исключается R₂. Получаем следующую симплекс-таблицу.

Итерация 1

БП	х1	х2	λ1	λ2	μ1	μ2	S1	S2	Реш.	Отн.
R1	2	0	2	1	-1	0	0	0	2	1
х2	0	1	-1/6	1/3	0	-1/6	0	0	1/2	–
S1	2	0	-1/6	1/3	0	-1/6	1	0	13/2	13/4
S2	1	0	1/3	-2/3	0	1/3	0	1	9	9
Оц.	-2	0	-2	-1	1	0	0	0

Т.к. μ₁=0, вводимой в базис переменной является быть х₁, при этом из числа базисных исключается R₁. Получаем следующую симплекс-таблицу.

Итерация 2

БП	х1	х2	λ1	λ2	μ1	μ2	S1	S2	Реш.
х1	1	0	1	1/2	-1/2	0	0	0	1
х2	0	1	-1/6	1/3	0	-1/6	0	0	1/2
S1	0	0	-13/6	-2/3	1	-1/6	1	0	9/2
S2	0	0	-2/3	-7/6	1/2	1/3	0	1	8

Итерация 2 даёт оптимальное решение рассматриваемой на этапе 1 задачи. Т.к. искусственные переменные вышли из базиса, то полученное решение х₁=1, х₂=1/2 являются допустимым. Оптимальное значение z вычисляется подстановкой полученного решения в выражение для целевой функции исходной задачи и равняется 7/4. ●

7.5. Графический метод решения задач НП. Так же как и в задачах ЛП, задачи с двумя переменными могут быть решены графически.

Пример 7. Найдём экстремумы функции z=x₁+2x₂ при ограничениях

≤9, х₁≥0, х₂≥0.

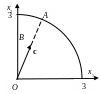
■ ОДР – часть окружности с радиусом 3, которая расположена в 1-й четверти (рис. 1). Линиями уровня целевой функции являются параллельные прямые x2=- x1+С (10) с угловым коэффициентом - . Проведём вектор =с=(λ;2λ) (где λ – любое положи-

Рис. 1

тельное число), перпендикулярный к каждой из линий уровня. Минимум достигается в точке О(0;0), а максимум в точке А касания окружности и вектора . Прямая ОА проходит через начало координат перпендикулярно прямым (10). Поэтому её уравнение x₂=2x₁. Решаем систему откуда находим x₁= , x₂= , z_max=3 . ●

Пример 8. Решим задачу нахождения экстремумов функции

z=

при ограничениях x₁+x₂5, 2x₁+x₂8, x₁≥0, x₂≥0.

■ Выделим полные квадраты в выражении для функции z:

z= = =

=25-(x₁-3)²-(x₂-6)².

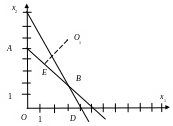
ОДР – 4-угольник ОАВD (рис. 2). Линиями уровня целевой функции являются концентрические окружности с центром в точке О₁(3;6) с радиусами 0r5. Минимум находится в точке О(0;0) как самой удалённой от точки О₁, и равен z_min=-20. Максимум находится в точке Е, как самой ближайшей к О₁ точки ОДР. Точка Е находится на пересечении прямой АВ x₁+x₂=5 и перпендикуляра к этой прямой, проведённого из точки О₁. Т.к. угловой коэффициент прямой x₁+x₂=5 равен -1, то угловой коэффициент перпендикуляра О₁Е равен 1. Из уравнения прямой, проходящей через данную точку О₁ с угловым коэффициен-

том 1, получим x2-6=x1-3, откуда x1-x2=-3. Решая систему находим координаты точки Е: x1=1, x2=4, при этом zmax=21. ● Пример 9. Решим задачу нахождения экстремумов функции z=
	Рис. 2

при ограничениях x₁x₂≥5, 0x₁5, 0x₂5.

■ Выделим полные квадраты в выражении для функции z:

z= =(x₁-7)²-(x₂-2)².

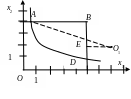
ОДР – фигура АВD (рис. 3), ограниченная гиперболой x₁x₂=5 (кривая АD) и двумя прямыми АВ и ВD. Линиями уровня целевой функции являются концентрические окружности с центром в точке О₁(7;2).

Максимум находится в точке А(1;5) как самой удалённой от точки О1, и равен zmax=45. Минимум находится в точке Е(5;2), как самой ближайшей к О1 точки ОДР, и равен zmin=4. ●
	Рис. 3