Приложение 8. Задачи по теме «Логика»

Даны следующие простые высказывания: А = {Число 3 является делителем числа 171}, B = {Коля Петров - отличник}, C = {Число 2 больше числа 3}, D = {Идет дождь}, и пусть A и B истинны, а С и D ложны. Применяя к данным элементарные операции отрицания, дизъюнкции, конъюнкции, эквиваленции и импликации, можно получить 34 сложных высказываний. Сколько среди них истинных?
По мишени произведено три выстрела. Пусть . Что означают следующие высказывания: а) б) в) г) ?
Какие из логических операций не будут иметь истинного значения, когда на входе операции все аргументы истинны? Сколько таких логических операций?
Какие из логических операций при обработке двух противоположных аргументов выдают различные значения, зависящие от порядка аргументов? Сколько таких логических операций?
Какие из логических операций будут иметь истинное значения, когда на входе операции все аргументы ложны? Сколько таких логических операций?
Какая формула соответствует высказыванию «для A достаточно B» (A и B – логические переменные)?
Какая формула соответствует высказыванию «для A необходимо B» (A и B – логические переменные)?
Какая формула соответствует высказыванию «неверно, что если C, то B» (C и B – логические переменные)?
Какая формула соответствует высказыванию «A тогда и только тогда, когда B» (A и B – логические переменные)?
Какая формула соответствует высказыванию «неверно, что A эквивалентно B» (A и B – логические переменные)?
Сформулируйте на естественном языке отрицание следующего высказывания, обосновав свою формулировку с помощью языка алгебры логики: "Если урок по информатике будет интересным, то никто из учеников - Петя, Витя, Кира не будет смотреть постоянно в окно".
Сформулируйте на естественном языке отрицание следующего высказывания: "Виктор пойдет на рыбалку только при солнечной погоде, если не будет жарко".
Мальчик решил в воскресенье закончить чтение книги, сходить в музей или кино, а если будет хорошая погода – пойти на реку выкупаться. В каком случае можно сказать, что решение мальчика не выполнено?
Пусть высказывания , , , . Прочитайте словесно следующие формулы: ; ; ; ; ; .
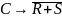, . Прочитайте словесно: ; ; ; ; ; ; ; . Какие формулы по содержанию истинны независимо от значений истинности x и y? Какие формулы истинны независимо от содержания высказываний x и y?
Припишите буквам некоторые математические высказывания так, чтобы формулы оказались истинными: .
Ни 7, ни 13 не являются четными числами. С помощью высказываний , запишите это сложное высказывание.
Докажите равносильность .