VII. Лабораторная работа № 12. Определение коэффициента внутреннего трения жидкости по методу стокса.

1. ТЕОРИЯ.

1. Понятие о вязкости.

Вязкость (внутреннее трение) – это одно из явлений переноса, обуславливающее диссипацию энергии при деформации вязкой среды.

Диссипация энергии – это переход энергии упорядоченных процессов, например: механической кинетической и потенциальной энергий в энергию неупорядоченных процессов, т.е. в тепловую энергию. Диссипация энергии происходит в результате совершения работы против сил трения, действующих между сдвигаемыми относительно друг друга слоями вязкой среды в процессе течения.

Для вязкости как физической величины существует несколько взаимосвязанных определений.

1. Вязкость–это коэффициент пропорциональности между силой трения, действующей на единицу площади трущихся слоев жидкости и градиентом скорости вдоль нормали к этим слоям (рис.7)

(VII.1),

где F- сила трения, S – площадь, - градиент скорости, - коэффициент динамической вязкости (или просто вязкость).

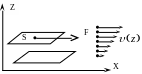
Рис.7

2.Вязкость – это коэффициент пропорциональности между плотностью потока импульса через какую-либо площадку и градиентом скорости вдоль нормали к этой площадке

(VII.2),

где L- импульс, t- время.

3. Вязкость– это коэффициент пропорциональности между тангенциальным напряжением и скоростью деформации сдвига.

(VII.3),

где -тангенциальное (сдвиговое) напряжение, F – сила, касательная к поверхности площадью S,  = dx/dz – относительная деформация сдвига, dx – относительное смещение двух слоев вязкой среды, отстоящих друг от друга на расстоянии dz за некоторое время.

3. Вязкость – это количество импульса L, переносимое за единицу времени через единицу площади при скорости сдвига d /dt, равной единице

(VII.4).

Студентам предлагается самостоятельно получить уравнения (VII.4), (VII.3), (VII.2) из исходного уравнения (VII.1).

Вязкие вещества, у которых вязкость  не зависит от скорости деформации d/dt , называются ньютоновскими. Отношение / где - плотность, называется кинематической вязкостью. Величину 1/ иногда называют текучестью.

2. Зависимость вязкости жидкостей и газов от параметров состояния.

Для идеального газа вязкость определяется частотой молекулярных соударений и выражается формулой:

,

где -плотность газа, -средняя арифметическая скорость молекул газа, -длина свободного пробега, m-масса одной молекулы, d-диаметр молекулы.

В таком газе вязкость зависит только от температуры  и при постоянной температуре не зависит ни от плотности, ни от давления. Разумеется, вязкость идеального газа косвенно зависит от давления или от плотности в таких процессах, когда температура изменяется в зависимости от давления или от плотности.

В жидкостях наблюдается совершенно иная, по сравнению с газами, зависимость вязкости от параметров состояния.

Для большинства жидкостей зависимость вязкости от температуры при постоянном давлении можно описать формулой Френкеля (в зарубежной литературе ее называют формулой Андраде).

= А(Т) е^{W /kT},

где k-постоянная Больцмана, W- энергия активации молекулярного скачка А (Т)- предэкспоненциальный множитель, слабо зависящий от температуры (по сравнению с экспонентой е^{W /kT}).

Практически множитель А(Т) можно заменить константой:

= А е^{W /kT} =А е^/Т (VII.5),

где = W/k –характеристическая температура. Из формулы (VII.5) следует, что вязкость жидкостей при повышении температуры резко уменьшается (рис.8.).

При постоянной температуре вязкость большинства жидкостей увеличивается при увеличении давления. Исключение со ставляет вода, у которой при температуре ниже 25⁰ С с ростом давления вязкость сначала уменьшается и проходит через минимум.

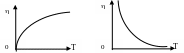а б

Рис.8. Зависимость вязкости идеального газа (а) и жидкости (б) от температуры.

Для простых жидкостей зависимость вязкости от объема при постоянной температуре достаточно хорошо описывается формулой Бачинского ,

где С – константа, b– несжимаемый объем одного моля, -объем одного моля.