VI. Лабораторная работа № 10. Определение коэффициента внутреннего трения воздуха капиллярным вискозиметром.

ВВЕДЕНИЕ.

Для определения вязкости газов часто применяют метод капиллярного вискозиметра. Если течение газа происходит через достаточно короткий капилляр, то давление, под которым находится газ у входа в капилляр, незначительно отличается от давления у выхода из капилляра. Тогда плотность газа вдоль оси капилляра остается практически неизменным, газ можно считать несжимаемым, и при ламинарном течении воздуха через капилляр для определения вязкости можно использовать формулу Пуазейля:

= (VI.1),

где  V—объем газа, протекающий через капилляр длиной l за время t,  Р — разность давлений на концах капилляра,  — коэффициент внутреннего трения газа, у= t  Р.

Порядок выполнения работы.

У становка (рис.6) состоит из газометра Г, манометра М, капилляра К и осушительной склянки С.

Рис. 6 Установка для определения вязкости воздуха

Газометр имеет краны 1,5,6,7. Кран 5 служит для наполнения газометра водой из воронки 2. Через кран 1 вода может выливаться из газометра. Через кран 6 газометр может соединяться с внешним пространством, а через кран 7 - с капилляром.

Водомерная трубка 4, позволяет определить объем вытекшей воды.

В газометре, из которого выливается вода, создается разряжение и возникает поток воздуха, втекающего из внешней среды через капилляр внутрь газометра. Манометром измеряют перепад давления на концах капилляра. Склянка С с хлористым кальцием или гранулами силикагеля служит для осушения воздуха перед его прохождением через капилляр.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1.Заполнить водой воронку газометра. При закрытых кранах 1 и 7 и при открытых кранах 5 и 6 заполнить водой полость газометра и закрыть краны 5 и 6.

2.Полностью открыть кран 7 и открыть кран 1. При этом из газометра через кран 1 начнет выливаться вода и по шлангу сбрасывается в водосток. Начнется просасывание воздуха через капилляр. Выждать, пока установиться почти постоянная разность уровней воды в манометре М.

3. Дождаться, пока уровень воды в водомерной трубке подойдет к очередному делению и по секундомеру определить время вытекания 0,5— 1,0 литра воды из газометра. В середине этого промежутка измерить разность уровней жидкости в манометре. Не останавливая тока воды, повторить измерения сколько возможно раз. Всего проделать 7-10 измерений, при необходимости повторно заполняя полость газометра водой.

ПОРЯДОК РАСЧЕТА.

При каждом очередном измерении давление между концами капилляра будет разное. Соответственно будет разным и время истечения очередной порции воды из манометра и при расчетах нельзя использовать средние значения давления и времени истечения, поскольку измерения повторялись не при одинаковых условиях. Однако даже в этих условиях произведение Y давления на время истечения будет оставаться постоянным. Поэтому для расчёта коэффициента вязкости воздуха в формулу (VI.1) следует подставить среднее значение этого произведения.

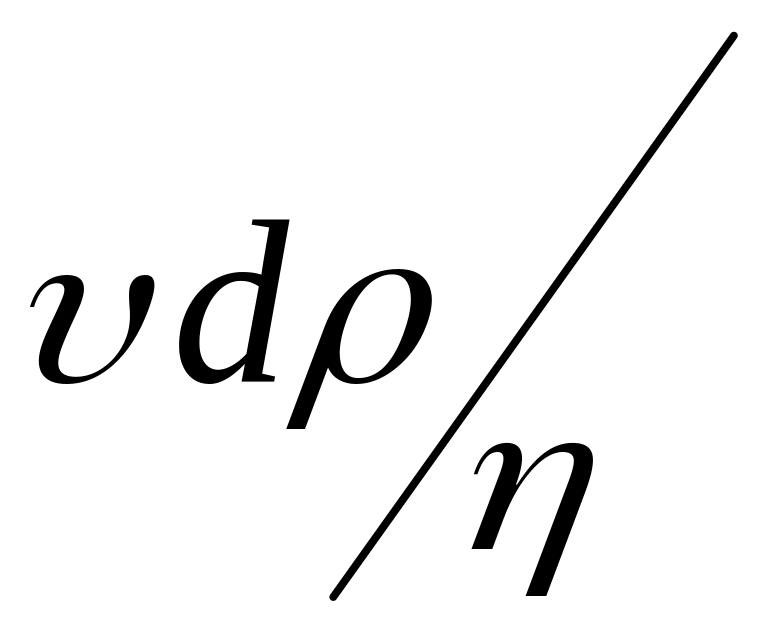
После получения величины коэффициента вязкости воздуха необходимо убедиться, что течение воздуха через капилляр было ламинарным. Течение будет ламинарным, если безразмерная величина Re =  1000. Здесь Re - число Рейнольдса, - средняя скорость течения газа, d - диаметр капилляра,  - плотность воздуха,  - коэффициент вязкости воздуха.

Величина средней скорости определяется из выражения: , плотность воздуха при комнатной температуре и данном атмосферном давлении можно рассчитать по уравнению Менделеева - Клапейрона.

Рекомендуемая форма таблицы измерений.

Т_комн = … , C⁰; Р_атм =…, мм рт. ст.

№№ опыта	Р мм вод.ст.	t c	у=t*P	у
1
2
3
4
5
6
7
8

Погрешность измерения вычисляется по формуле:

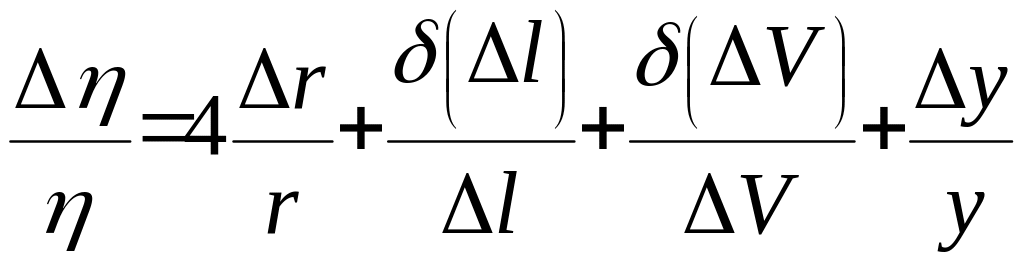
КОНТРОЛЬНЫЕ ВОПРОСЫ:

0. Каковы физическое содержание и размерность коэффициента вязкости ?

1. Какова зависимость коэффициента вязкости  от макроскопических параметров газа?

2. Что такое число Рейнольдса?

ЛИТЕРАТУРА.

1. И.К. Кикоин А.К. Кикоин ''Молекулярная физика '' §§ 8,9.

2. Стрелков ''Механика'' Наука, 1965, гл.12, § 111