V. Лабораторная работа № 7. Определение коэффициента теплопроводности воздуха.

Теория.

Перенос тепла от более нагретой части какого-либо тела к менее нагретой может осуществляться тремя способами: теплопроводностью, конвекцией и электромагнитным (в основном инфракрасным при температурах не на много выше комнатной) излучением. В случае теплопроводности количество тепла dQ, проходящее через площадку dS за время dt определяется уравнением

dQ = (V.1)

где — градиент температуры вдоль оси х, перпендикулярной площадке S,  — коэффициент теплопроводности данной среды. Для газов кинетическая теория приводит к следующему выражению для теплопроводности

 = vс_V = k (V.2)

где — плотность газа, v— средняя скорость теплового движения молекул газа, —средняя длина свободного пробега молекул газа, с_V —удельная теплоемкость при постоянном объеме, К—константа для данного газа, не зависящая от температуры, Т— абсолютная температура.

Конвекция возникает в том случае, если температура газа понижается с высотой из-за того, что легкий нагретый газ поднимается вверх, а на его место опускается более холодная масса газа. Конвекция усиливается при увеличении плотности газа, при увеличении геометрических размеров системы и увеличении разности температур. При всякой заданной геометрии прибора конвекция возникает скачком, при достижении некоторой разности температур Т. При измерении теплопроводности газов влияние конвекции можно уменьшить, используя в качестве измерительной ячейки длинную узкую вертикально расположенную металлическую трубку, по оси которой натянута тонкая проволока, нагреваемая электрическим током. В этом случае возникновению конвекции препятствует вязкость газов.

Для оценки количества тепла, отдаваемого проволокой за счет излучения, можно использовать закон Стефана- Больцмана:

N_изл= (V.3),

где площадь поверхности проволоки, Т₁ и Т₂ - абсолютные температуры проволоки и трубки соответственно,

 = 5,735 *10^-8 Вт/м²к⁴ — постоянная Стефана- Больцмана,  — средняя поглощательная способность электромагнитного излучения поверхностью проволоки. Для меди  = 0,8, для никеля

 = 0,4.

Рассчитаем поток тепла за счет теплопроводности от нагретой проволоки к стенкам трубки. При установившейся температуре через любую воображаемую цилиндрическую поверхность радиуса r между проволокой и трубкой (рис.5) проходит за единицу времени одно и то же количество тепла:

N =

где — длина проволоки. Если разность температур проволоки и трубки не является малой, то следует учесть зависимость коэффициента теплопроводности от температуры согласно (V.2). После преобразования с учетом (V.2) получим:

.

Проинтегрируем это выражение:

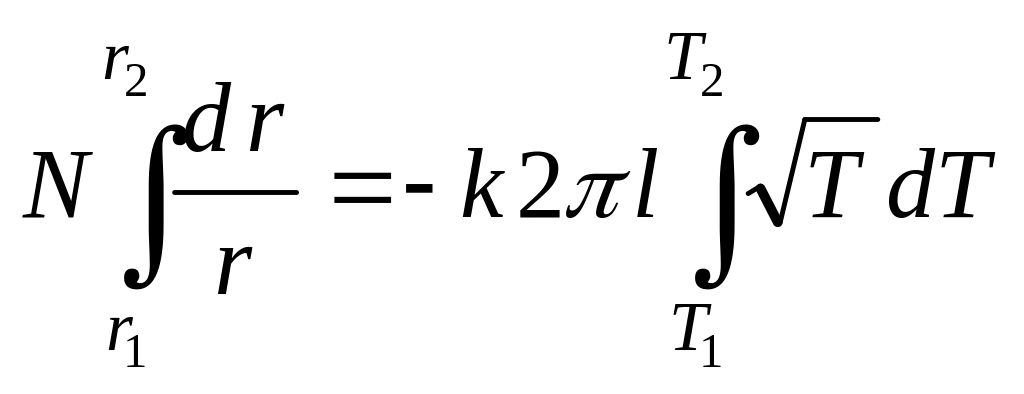
где r₁ — радиус проволоки . r₂ — внутренний радиус трубки.

Р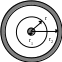 ис.4. К расчёту потока тепла от нагретой проволоки к стенкам трубки.

После интегрирования и подстановки пределов получим:

T₁^3/2 = T₂^3/2 + k₁N , где k₁ = (V.4).

Видно, что величина T₁^3/2 линейно зависит от мощности теплового потока N.

Построив график зависимости T₁^3/2 =f (N) можно по угловому коэффициенту полученной прямой определить константу k₁ и по (V.4) и (V.2) рассчитать теплопроводность газа.

Описание экспериментальной установки.

Схема установки приведена на рис.5

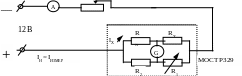
Рис.5. Экспериментальная установка для измерения коэффициента теплопроводности воздуха.

Измерительная ячейка состоит из массивной металлической трубки, по оси которой натянута тонкая никелевая проволока, нагреваемая электрическим током. Температура проволоки определяется по величине электрического сопротивления проволоки, измеряемой с помощью моста постоянного тока Р329. Для никеля зависимость сопротивления от температуры в интервале 0 –200 С⁰ определяется с погрешностью не более 0,5 С⁰ следующими уравнениями:

R_x /R₀ =1+5,33*10^-3Т₁+8,3*10^-6Т₁²+… (V.5)

Т₁=178,5  -26,5 ² +…, где  = R_x /R₀ -1 (V.6),

где Т₁ – температура никелевой проволоки.

R_x – сопротивление при этой температуре.

R₀ – сопротивление при температуре 0 С⁰.

Для определения температуры проволоки по формуле (V.6) необходимо знать ее начальное сопротивление при какой-либо известной температуре и по формуле (V.5) посчитать R₀. Однако, любой ток, протекающий через проволоку при измерении ее сопротивления, нагревает ее. Нагрев можно уменьшить, уменьшив силу тока, но в этом случае уменьшится точность измерения сопротивления. Проблему можно решить, произведя несколько измерений сопротивления при разных сравнительно небольших токах. Тогда, экстраполировав график зависимости сопротивления от мощности N_пров= I² R к точке N_пров= 0, получим сопротивление при комнатной температуре Т_к.

Порядок выполнения работы.

1. Убедиться, что кнопки ’’грубо’’, ’’точно’’ и ’’успокоение’’ моста Р329 отжаты.

2. Включить источник питания измерительной ячейки и реостатом выставить силу тока по амперметру I_A=0,2 A. Нажимая кнопки ’’грубо’’, а затем ’’плавно’’, ручками установки R₁ моста сбалансировать мост. Рассчитать сопротивление проволоки R_х: R_х = R_N* R₁/ R₂

где R_N , R₁ , R₂ – сопротивления плеч моста, R_N –нормальное сопротивление, т.е. эталонное сопротивление моста

3. Повторить измерения сопротивления проволоки при других токах I_А. При этом после каждого измерения тока необходимо подождать пока сопротивление проволоки перестанет изменяться.

4. Для всех токов I_А найти силу тока I_х, протекающего через проволоку:

I_х =

5. Для токов, не превышающих 0,5 А, построить график зависимости R_х= f(I_x²R_x) и по нему путем экстраполяции к точке I_x²R_x= 0 определить сопротивление R_к при комнатной температуре Т_к.

6. По формуле (V.5) определить R₀ , подставив вместо R₀ и Т₁ соответственно R_к и Т_к

7. Для всех токов найти температуру проволоки (формула V.6), мощность излучения (формула V.3). Построить график T₁^3/2= f (N), где N=I_x²R_x- N_изл

8. По угловому коэффициенту графика определить константу k1 и по (V.4) и (V.2) рассчитать теплопроводность воздуха при температурах 0 ⁰С и 20 ⁰С.

Рекомендуемая форма таблицы измерений:

R_N =…, Ом ; R₂=…, Ом; L =…, мм; r₁=…, мм;

r₂=…, мм; Т_комн = … , C⁰; P =…, мм рт. ст.

IA, A	Rx, Ом	Tx, C0	Ix2Rx, Вт	Nизл, Вт	N, Вт	Тх3/2, К3/2
0,2 0,3 0,4 0,5 0,6 0,7 0,8 1,0 1,2 1,4

-относительное изменение сопротивления проволоки по отношению к сопротивлению при Т₀=0 С^0.