III. Лабораторная работа № 5. Определение отношения теплоемкостей ср/сv газов методом адиабатического расширения.

1. ТЕОРИЯ МЕТОДА.

Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме: =С_Р / C_V является важной характеристикой газов. Для идеального газа это отношение связано с эффективным числом i_эф степеней свободы молекул газа:

 = (i_эф +2) / i_эф (III.1).

Описываемый ниже способ определения этого отношения достаточно прост.

Пусть мы имеем стеклянный сосуд, содержащий исследуемый газ. Сосуд соединен с жидкостным (водяным) манометром, а посредством крана может соединяться с атмосферой. Если накачать в сосуд небольшое дополнительное количество газа, то давление в сосуде повысится. При быстром сжатии газа температура его так же повысится. Окончательное давление газа Р₁ в сосуде установится, когда его температура сравняется благодаря теплопроводности стенок с температурой окружающего воздуха Т_0. Это состояние (Т₀ , Р₁) назовем первым состоянием газа.

Давление р₁ можно выразить через разность уровней жидкости h₁ в манометре:

Р₁ = Р₀ + k h₁, (III.2).

где Р₀ - атмосферное давление, k – размерный коэффициент.

Если теперь быстро открыть кран, то газ из сосуда будет выходить в атмосферу и адиабатически расширяться, пока давление его в сосуде не сделается равным Р₀. При этом он охладится до температуры Т₂; это будет вторым состоянием газа (состояние Т₂, Р₀).

Если сразу после открывания снова закрыть кран, то давление внутри сосуда начнет возрастать вследствие того, что охладившийся при расширении газ станет снова нагреваться. Возрастание давления прекратиться, когда температура газа в сосуде сравняется с внешней температурой Т₀; это будет третьим состоянием газа (состояние Т₀, Р₂).

Давление р₂ так же можно выразить через разность уровней жидкости h₂ в манометре:

Р₂ = Р₀ + k h ₂ (III.3).

Так как переход от состояния 2 к состоянию 3 произошел без изменения объема, то мы вправе применить здесь закон Гей-Люссака

(III.4).

К адиабатическому процессу перехода из состояния 1 в состояние 2, может быть применен закон Пуассона, который удобно написать в следующей форме:

. (III.5).

Подставляя сюда значения Р₁ из уравнения (III.2) и переставляя члены, получим

.

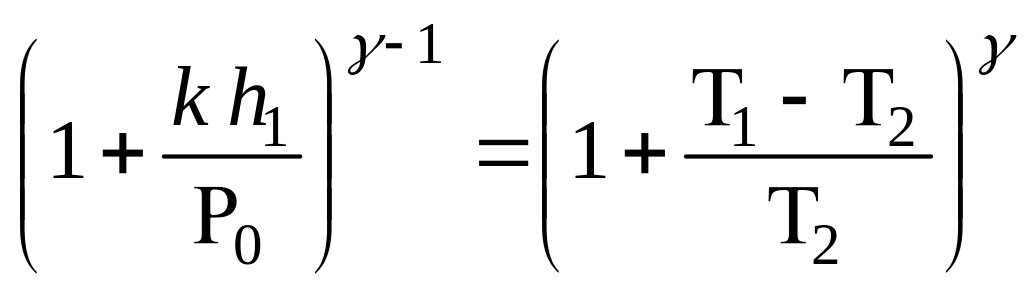Так как k h₁ /P₀ и (Т₁-Т₂) /Т₂ — величины малые по сравнению с единицей, то, разлагая оба двучлена в ряд Тейлора и ограничиваясь членами первого порядка малости, получим приближенную формулу:

.

Подставив в уравнение (III.4) значение Р₂ из уравнения (III.3), получим

, .

Окончательно находим: (III.6)

2. ОПИСАНИЕ ПРИБОРА.

Прибор (рис.2) состоит из стеклянного баллона, соединенного шлангами с манометром М и насосом Н. Через кран К баллон может сообщаться с атмосферой. Из-за того, что сжатый газ из баллона через кран К выходит в течение определенного промежутка времени, не равного нулю, процесс расширения газа от 1-го состояния ко 2-му нельзя считать строго адиабатическим. При этом ошибка будет тем меньше, чем меньше времени кран К находится в открытом положении. Разумеется, это время должно быть достаточно для выравниваний давлений внутри и вне баллона. Для избежания указанной ошибки рекомендуется повторить опыт несколько раз, меняя время выдержки t клапана в открытом положении, и графически экстраполировать полученные отношения к промежутку времени t = 0.

Наиболее удобными для экстраполяционного графика являются координаты ln (h₂ / h₁ ) = f (t), в которых график имеет вид почти прямой линии.

Н

М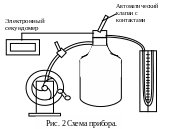

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Закрыть кран К и насосом Н накачать в баллон воздух до давления на 300 мм водяного столба выше атмосферного давления.

1. Выждать 1-2 минуты, пока давление установиться, измерить начальную разность уровней жидкости h₁ в манометре и занести в таблицу

2. Открыть кран на требуемый промежуток времени t. Рекомендуемые значения t, с: 2.5, 3, 4, 5, 7, 10, 15. Фактическое значение t измерить по электронному секундомеру и занести в таблицу

3. Выждать 1-2 минуты, пока давление перестанет меняться, измерить конечную разность уровней жидкости h₂ в манометре и занести в таблицу.

4. Опыт повторить 7 раз, каждый раз устанавливая одинаковое начальное давление (с точностью 10 мм водяного столба) и увеличивая время выдержки t крана в открытом положении.

5. По полученным данным нанести точки графика зависимости ln (h₂ / h₁ )=f(t). На графике провести прямую, лучше всего соответствующую всей совокупности точек, Для этой прямой определить отношение h₂ / h₁, которое соответствует t=0.

6. Для сравнения рассчитать отношение h₂ / h₁ на компьютере, выполнив по методу наименьших квадратов линейную аппроксимацию полученной зависимости ln (h₂ / h₁ ) от t.

7. Полученное значение h₂ / h₁ подставить в формулу (III.6) и рассчитать значение .

8. По значению из формулы (III.1) определить среднее эффективное число степеней свободы i_эф молекул воздуха.

9. Полученные значения и i_эф сравнить с теоретическими значениями для двухатомных газов. Сформулировать выводы.

Рекомендуемая форма таблицы результатов измерений

№	h 1, мм	t, с	h 2, мм	h2 / h1	Ln(h2 / h1 )
1
2
3
4
5
6
7

КОНТРОЛЬНЫЕ ВОПРОСЫ .

1. Теплоемкость. Виды теплоемкости. Соотношения между ними.

2. Распределение энергии по степеням свободы молекул газа. Особенности этого распределения при разных температурах.

3. Стандартные процессы в газах; их уравнения и графики в различных координатах.

4. Из (III.2) - (III.5) получить точную формулу для .

ЛИТЕРАТУРА.

А. Н. Матвеев ‘‘Молекулярная физика ’’ М.,1987 г. §§ 10, 12, 19, 22, 23.