Приложение 1.

ИНТЕНСИВНЫЕ ВЕЛИЧИНЫ (ПАРАМЕТРЫ) в термодинамике -параметры системы, не зависящие от массы системы, т.е. имеющие одинаковые значения для всей однородной системы и любой ее макроскопической части.

ЭКСТЕНСИВНЫЕ ВЕЛИЧИНЫ (ПАРАМЕТРЫ) в термодинамике - параметры системы, пропорциональные массе системы или ее объему. Обладают свойством аддитивности, т.е. Э.П. всей однородной системы равны сумме Э.П. ее макроскопических частей.

ЯВЛЕНИЯ ПЕРЕНОСА - необратимые процессы, в результате которых в физической системе происходит пространственный перенос какой-либо ЭКСТЕНСИВНОЙ ВЕЛИЧИНЫ (массы, энергии, импульса, электрического заряда и др.). Движущей силой Я.П. является неодинаковое значение ИНТЕНСИВНЫХ ПАРАМЕТРОВ в разных частях системы (плотности, температуры, скорости, электрического потенциала). Я.П. происходят в таком направлении, чтобы выровнять интенсивные параметры, т.е. приблизить систему к состоянию равновесия.

ПОТОК какой-либо экстенсивной физической величины Q через какую-либо воображаемую поверхность- это скалярная величина, равная количеству величины Q, переносимой за единицу времени через всю эту поверхность.

поток Q= dQ/dt

ПЛОТНОСТЬ ПОТОКА какой-либо экстенсивной физической величины Q через какую-либо воображаемую поверхность- это векторная величина, равная количеству величины Q, переносимой за единицу времени через единицу площади поверхности, перпендикулярной направлению потока и направленная по направлению потока

J_Q = dQ / dt S

В линейном приближении плотность потока пропорциональна градиенту интенсивной величины:

J_Q = -К grad P

Приложение 2.

ЗАКОН О РАСПРЕДЕЛЕНИИ ЭНЕРГИИ ПО СТЕПЕНЯМ

СВОБОДЫ.

В состоянии термодинамического равновесия на каждую квадратичную форму энергии каждой степени свободы термодинамической системы приходится в среднем одинаковая энергия, равная ½ КТ.

Квадратичная форма энергии - это каждое слагаемое энергии системы, пропорциональное квадрату какой-либо обобщенной координаты или скорости.

Число степеней свободы термодинамической системы- это число независимых координат, определяющих положение всех частиц системы в пространстве. На каждый атом системы приходится 3 степени свободы.

КЛАССИЧЕСКАЯ ФОРМУЛИРОВКА ЗАКОНА РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ

В состоянии термодинамического равновесия на каждую квадратичную форму энергии каждой степени свободы системы приходится в среднем энергия, равна l/2 KT.

ПОЯСНЕНИЕ: квадратичной формой энергии называется каждое слагаемое полной энергии системы, пропорциональное квадрату какой-либо обобщенной координаты или обобщенной скорости.

ДОПОЛНЕНИЕ: на линейные формы энергии (пропорциональные обобщенным коорди­натам, например Е_потенц=mgz ), если эта координата может меняться в интер­вале от 0 до ∞, приходится в среднем энергия, равная КТ.

ПРИМЕР. Полная сумма слагаемых средней энергии двухатомной молекулы в поле тяжести Земли в атмосфере или в вертикальном сосуде неограниченной высоты:

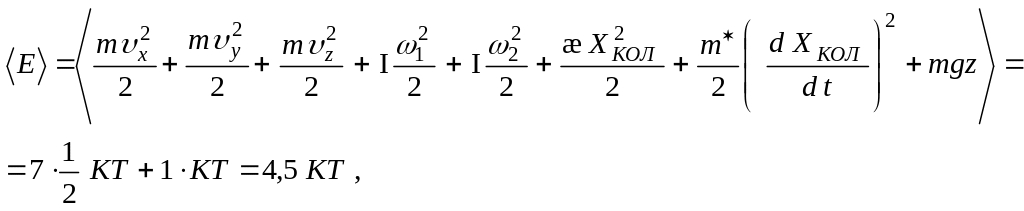
где Х_КОЛ - колебательная координата, χ - коэффициент квазиупругой силы, m* -приведенная масса, I - момент инерции, ω₁ и ω₂- угловые скорости вращения относительно двух осей, перпендикулярных оси молекулы.

Если газ находится в сосуде ограниченной высоты, малой по сравнению с < Z > =KT/mg , то последнее слагаемое < mqz > средней энергии исчезает. При нормальных температурах, которые << Т_колеб, исчезают так же 2 слагаемых колебательной энергии. Остается <Е>=2,5 КТ. Согласно законам квантовой механики разрешенные значения вращательной (rotation) энергии (Е_г) и колебательной (vibration) (E_v) энергий молекул определяются из формул:

, где - разрешенные значения момента импульса, I - момент инерции, r = 0.1.2,3... - вращательное квантовое число

, где ω - циклическая частота колебаний,

v = 0.1,2.3...- колебательное квантовое число.

Заметный вклад соответствующих видов движения в теплоемкость появляется при температуре Т, определенной из условия:

K T_ВРАЩ = Е_{r =1} – Е_{r =0} =∆ Е_ВРАЩ 1,0 ≈ единицы ÷ десятки Кельвин

К Т_колеб = Е_{v =1}- Е_{v =0} =∆ Е_колеб 1,0 ≈ тысячи Кельвин

ћ