Вычисление средней гармонической
Средняя
гармоническая простая:
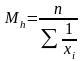
Задача 2.9 [5]. 5 доярок в течение 1 часа ручным способом надоили следующее количество молока: 10, 20, 25, 30, 20 – всего 105 л. Сколько времени затрачивает в среднем доярка на выдаивание 1 л молока?
М = 105/5 = 21 л. t= 60 / 21 = 2,86 мин. |
Мh =5 /(1/10 +1/20 +1/25 +1/30 +1/20) = 5 /0,273 = 18,31 л t = 60/18,31 = 3,23 мин. |
Средняя
гармоническая взвешенная:
.
Задача 2.10 [5].
Плотность колосьев ржи = (кол-во зерен в колосе) / (длина колоса). Объем выборки – 20 растений |
Длина колосьев |
8 |
9 |
10 |
11 |
12 |
Кол-во зерен в колосе |
36 |
38 |
40 |
41 |
42 |
|
Частота (n = 20) |
2 |
5 |
10 |
2 |
1 |
|
Плотность колосьев |
4,5 |
4,2 |
4,0 |
3,7 |
3,5 |
Средняя плотность колосьев в выборке:
Мh= 20 / (2×1/4,5 + 5×1/4,2 + 10×1/4,0 + 2×1/3,7 + 1×1/3,5) = 20 / 5 = 4.
Сравните: М = (2×4,5 + 5×4,2 + 10×4,0 + 2×3,7 + 1×3,5) / 20 = 81/20 = 4,1.
Вычисление средней квадратической
Применяется при выражении признаков мерами площади
Средняя
квадратическая простая
;
взвешенная
.
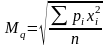Задача 2.11 [5].
Измерялся – диаметр корзинок подсолнуха в см., n = 10 |
Диаметр корзинок (xi) |
8 |
11 |
13 |
15 |
16 |
17 |
Число случаев (pi) |
1 |
1 |
2 |
3 |
2 |
1 |
Средний размер признака
1×82+1×112
+2×132
+3×152
+2×162
+1×172
=1999.
14,1
см.
Сравните: М = (1×8 +1×11 +2×13 +3×15 +2×16 +1×17) / 10 = 139 /10 = 13,9 см.
Вычисление средней кубической
Применяется при выражении признаков мерами объема.
Средняя кубическая
простая
;
взвешенная
.
Задача 2.12 [5]. Измерялся диаметр
яиц в мм [полусумма большого и малого диаметров], n = 18 яиц |
Диаметр яиц (xi) |
47 |
48 |
50 |
54 |
56 |
60 |
Число случаев (pi) |
2 |
4 |
6 |
3 |
2 |
1 |
Средний размер признака
2×473
+ 4×483
+ 6×503
+ 3×543
+ 2×563
+ 1×603
= 24397;
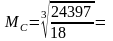51
мм.
Вычисление средней геометрической
Применяется при увеличении линейных размеров тела, прироста численности популяции за определенный промежуток времени
Средняя
геометрическая 
обычно вычисляется с помощью десятичных логарифмов по формуле
.
Задача 2.13 [5]. Живая масса подопытных мышей изменяется с возрастом. Средняя геометрическая недельных абсолютных прибавок массы мышей за первые 9 недель их жизни lgМg =7,58895/8 =0,94861,
Мg = 8,9 г.
Сравните: М =77/9 = 9,6 г. |
Возраст мышей (неделя) |
Живая масса, г, xi |
Абсолютные недельные прибавки массы, г |
Логарифм прибавок массы |
1 |
10 |
- |
- |
|
2 |
15 |
5 |
0,69897 |
|
3 |
20 |
5 |
0,69897 |
|
4 |
27 |
7 |
0,84510 |
|
5 |
35 |
8 |
0,90309 |
|
6 |
46 |
11 |
1,04139 |
|
7 |
58 |
12 |
1,07918 |
|
8 |
72 |
14 |
1,14613 |
|
9 |
87 |
15 |
1,17609 |
|
Сумма |
|
77 |
7,58892 |
Если признак варьируется непрерывно и выборка группируется в интервальный вариационный ряд, то
где Qi =x2 / x1 lgМg = 0,93806 / 8 = 0,1173,
Мg = 1,310 г.
Сравните: Мi =10,50/8 =1,313 г. |
Возраст мышей (неделя) |
Живая масса, г, xi |
Относительные недельные прибавки массы, г, Q |
Логарифм прибавок массы lgQ |
1 |
10 |
- |
- |
|
2 |
15 |
1,50 |
0,17609 |
|
3 |
20 |
1,33 |
0,12385 |
|
4 |
27 |
1,35 |
0,13033 |
|
5 |
35 |
1,30 |
0,11394 |
|
6 |
46 |
1,31 |
0,11727 |
|
7 |
58 |
1,26 |
0,10037 |
|
8 |
72 |
1,24 |
0,09342 |
|
9 |
87 |
1,21 |
0,08279 |
|
Сумма |
|
10,50 |
0,93806 |
,
Используют также
следующую формулу:
.
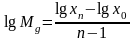Задача 2.14 [5]. Селекция гибридного хлопчатника за 5 лет позволила увеличить длину волокна с 26,3 мм до 31,0 мм. Определить среднегодовой эффект.
.
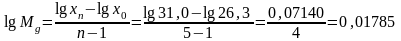Мg = 0,1044мм → 10,44% → Среднегодовой эффект: 10,44/5 = 2,1%.
Вычисление
коэффициента вариации:
.
Задача 2.15 [5]. На кролиководческой ферме взвешивание 35 животных показало следующий результат: |
3,0 |
2,7 |
2,1 |
1,6 |
1,2 |
1,6 |
2,2 |
2,1 |
2,3 |
1,5 |
1,1 |
2,2 |
2,5 |
2,4 |
|
1,9 |
2,1 |
2,3 |
1,3 |
1,0 |
1,8 |
1,9 |
|
1,8 |
3,2 |
2,1 |
2,9 |
3,0 |
1,3 |
1,9 |
|
2,6 |
1,5 |
2,4 |
2,7 |
1,9 |
2,0 |
2,6 |
Сравнить V двух выборок – 35 кроликов и 64 поросят (см. задачу 2.8).
Vкроликов = 27,3%, Vпоросят = 22,5%.