Меры центральной тенденции
Величины, отражающие все результаты измерений в распределении, называются центральной тенденцией. Тремя характеристиками центральной тенденции являются: среднее, медиана и мода. Среднее (M) – это среднее арифметическое, которое находится путем сложения всех результатов (Σxi ) и деления полученной суммы на количество результатов (n).
Медиана (Me) – это значение, расположенное в центре распределения и разделяющее все наблюдения на две половины. Мода (Mo) – это величина или категория, которая появляется наиболее часто. Среднее отклонение (более подробно см. ниже) вычисляют по следующей формуле:
Задача 2.5. Каков средний возраст женщин, участвовавших в исследовании? Поскольку мы исключаем из этого анализа мужчин, то должны подсчитать только те результаты в графе возраст, которым соответствует числовое значение 2 в графе пол (номера в этом анализе не нужны; они приведены в качестве справки)
|
Номер |
Возраст (xi) |
X1 |
X4 |
|
3 |
17 |
|
5 |
23 |
|
7 |
18 |
|
8 |
32 |
|
9 |
22 |
|
10 |
20 |
|
12 |
18 |
|
15 |
19 |
|
п = 9 |
Σxi = 206 |
.
Оценка изменчивости
Стандартное отклонение (standard deviation – SD) – это один из наиболее часто используемых показателей того, насколько величины отличаются от среднего. Формула для вычисления стандартного отклонения:
.
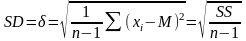Задача 2.6. Каково стандартное отклонение для количества часов, отработанных в неделю мужчинами?
Выберите из графы отработанные часы данные по мужчинам (мужчинам в графе пол соответствует числовое значение 1).
Подсчитайте для этой группы среднее арифметическое М.
Вычислите отклонение D – отнимите среднее значение от количества часов, отработанных каждым человеком D=(xi – M),
Возведите в квадрат каждую из полученных величин D2=(xi – M)2.
Вычислите сумму квадратов отклонений SS = ΣD2.
Подставьте эти величины в формулу SD.
-
X1
X7
Номер
Отработанные часы (xi)
D
D2
1
38
12
144
2
15
–11
121
4
30
4
16
6
35
9
81
11
20
–6
36
13
30
4
16
14
30
4
16
16
10
–16
256
n = 8
Σxi = 208
SS = 686
Помимо средней арифметической нередко требуется определить среднее гармоническое, квадратическое, кубическое, а так же их средневзвешенные значения. В приведенных ниже примерах ознакомимся с ними.
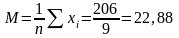