6. Использование формулы Грина для определения координат центра тяжести пластинок сложной формы в плане
При определении координат центра тяжести пластинок требуется вычислить интегралы по площади фигуры:
, (18)
где
—
поверхностная плотность.
Для вычисления
интегралов в том случае, когда пластинка
имеет контур сложной формы, можно
использовать прием, основанный на
применении формулы Грина. Формула Грина
позволяет свести интегрирование по
площади к интегрированию по замкнутому
контуру, ограничивающему эту площадь.
А именно: пусть C
— положительно ориентированная
кусочно-гладкая замкнутая кривая на
плоскости, а D
— область, ограниченная кривой C.
Если функции P
= P(x,y),
Q
= Q(x,y)
определены в области D
и имеют непрерывные частные производные
,
то справедливо равенство (формула
Грина):
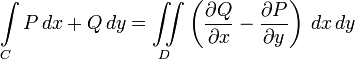. (19)
Очень часто проводить вычисления центра тяжести и других характеристик сечений (площадь, статические моменты, моменты инерции) удобно численно. При этом сложный контур можно представить в виде замкнутой ломанной, состоящей из множества отрезков. Чем больше степень разбиения криволинейных участков контура набором отрезков, тем выше точность приближения вычисленных значений к точным. Так же выражение для поверхностной плотности можно приблизить степенной функцией.
Тогда для численного
вычисления интегралов нужно иметь
формулы для вычисления
,
,
и т.д.
Ниже приведен ряд подобных формул с указанием того, какой вариант функций P = P(x,y), Q = Q(x,y) был использован при их построении.
.
(20)
;
(21)
; (22)
;
(23)
;
(24)
(25)
Суммирование ведется по всем отрезкам ломанной, и точки (x1 y1) – (x2 y2) – координаты очередного отрезка.
Так как ломанные
составляют замкнутый контур, то слагаемые
вида
для одного отрезка взаимно уничтожатся.
Вариант назначения функций P
= P(x,y),
Q
= Q(x,y)
влияет на
полученную формулу с точностью до
взаимно уничтожаемых слагаемых на
замкнутом контуре.
Варианты заданий расчетно-графической работы
по теме «Центр тяжести»
Определить центр тяжести сплошной фигуры, номер рисунка выбрать из предпоследней цифры шифра. В таблице, расположенной под рисунком выбрать номер условия по последней цифре шифра. Например, если шифр заканчивается на 45, то берут рис. 4 и условие 5.
№1
№2
№1
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
30 |
30 |
24 |
30 |
36 |
12 |
9 |
18 |
15 |
12 |
r(мм) |
15 |
12 |
12 |
18 |
18 |
6 |
6 |
12 |
12 |
6 |
a(мм) |
60 |
30 |
40 |
54 |
60 |
16 |
16 |
24 |
28 |
19 |
b(мм) |
40 |
25 |
40 |
30 |
42 |
0 |
10 |
0 |
6 |
3 |
№3
|
0 |
1 |
2 |
3 |
4 |
5
№4
|
6 |
7 |
8 |
9 |
r(мм) |
12 |
15 |
18 |
21 |
24 |
30 |
24 |
27 |
36 |
21 |
a(мм) |
18 |
0 |
72 |
60 |
80 |
60 |
54 |
56 |
62 |
50 |
b(мм) |
20 |
20 |
24 |
50 |
48 |
24 |
21 |
20 |
24 |
18 |
c(мм) |
12 |
16 |
16 |
10 |
20 |
30 |
60 |
28 |
25 |
24 |
№5
№6
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
20 |
45 |
24 |
45 |
30 |
27 |
24 |
21 |
16 |
30 |
a(мм) |
10 |
20 |
18 |
35 |
15 |
12 |
15 |
10 |
12 |
20 |
№8
№7
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
30 |
27 |
24 |
21 |
18 |
60 |
60 |
54 |
54 |
30 |
r(мм) |
15 |
15 |
12 |
12 |
9 |
30 |
42 |
27 |
30 |
18 |
a(мм) |
60 |
50 |
60 |
48 |
40 |
120 |
100 |
90 |
100 |
60 |
b(мм) |
100 |
80 |
92 |
64 |
72 |
20 |
20 |
30 |
28 |
40 |
№10
№9
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
φ(рад) |
0 |
|
|
|
|
|
|
|
|
|
R(мм) |
30 |
27 |
24 |
30 |
27 |
21 |
27 |
24 |
30 |
18 |
r(мм) |
18 |
12 |
18 |
15 |
15 |
10 |
15 |
12 |
15 |
10 |
a(мм) |
20 |
16 |
20 |
18 |
12 |
20 |
10 |
16 |
30 |
16 |
№12
№11
№12
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
30 |
24 |
27 |
21 |
36 |
30 |
36 |
45 |
36 |
45 |
r(мм) |
15 |
12 |
15 |
12 |
20 |
15 |
20 |
20 |
24 |
24 |
a(мм) |
32 |
30 |
30 |
27 |
42 |
70 |
72 |
80 |
32 |
78 |
b(мм) |
10 |
20 |
15 |
15 |
20 |
30 |
30 |
40 |
36 |
30 |
c(мм) |
30 |
10 |
10 |
20 |
15 |
10 |
12 |
12 |
10 |
20 |
d(мм) |
15 |
18 |
13 |
10 |
12 |
12 |
12 |
16 |
20 |
16 |
№13
№14
№13
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r(мм) |
12 |
18 |
15 |
6 |
9 |
12 |
15 |
18 |
21 |
9 |
R(мм) |
15 |
12 |
18 |
9 |
6 |
24 |
30 |
30 |
48 |
20 |
a(мм) |
50 |
36 |
48 |
30 |
24 |
50 |
60 |
64 |
50 |
40 |
№15
№16
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
20 |
10 |
9 |
6 |
12 |
15 |
21 |
15 |
27 |
30 |
r(мм) |
30 |
15 |
18 |
36 |
24 |
21 |
32 |
36 |
40 |
36 |
a(мм) |
50 |
50 |
45 |
34 |
48 |
35 |
39 |
45 |
49 |
50 |
b(мм) |
10 |
20 |
12 |
15 |
13 |
20 |
10 |
6 |
8 |
15 |
c(мм) |
30 |
25 |
30 |
40 |
50 |
25 |
50 |
40 |
60 |
70 |
d(мм) |
20 |
10 |
15 |
30 |
20 |
15 |
30 |
20 |
18 |
20 |
e(мм) |
30 |
35 |
30 |
40 |
30 |
25 |
30 |
40 |
30 |
35 |
№17
№18
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
30 |
27 |
24 |
36 |
24 |
40 |
45 |
50 |
42 |
38 |
r(мм) |
20 |
15 |
15 |
20 |
12 |
20 |
30 |
35 |
20 |
18 |
a(мм) |
25 |
25 |
20 |
24 |
15 |
25 |
35 |
32 |
40 |
20 |
№19
№20
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
R(мм) |
30 |
24 |
30 |
21 |
24 |
21 |
30 |
27 |
24 |
21 |
r(мм) |
15 |
15 |
18 |
12 |
18 |
12 |
18 |
15 |
12 |
15 |
a(мм) |
100 |
100 |
90 |
80 |
80 |
63 |
180 |
80 |
90 |
86 |
b(мм) |
40 |
30 |
45 |
30 |
24 |
22 |
60 |
40 |
24 |
22 |
α(рад) |
|
|
|
|
|
|
|
|
|
|
№21
№22
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r(мм) |
15 |
|
|
|
|
|
|
|
|
|
a(мм) |
30 |
36 |
40 |
32 |
50 |
24 |
20 |
24 |
18 |
24 |
b(мм) |
40 |
30 |
50 |
40 |
50 |
15 |
20 |
15 |
40 |
30 |
α(мм) |
|
|
|
|
|
|
|
|
|
|
№24
№23
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r(мм) |
30 |
27 |
24 |
21 |
30 |
50 |
40 |
25 |
18 |
60 |
a(мм) |
32 |
30 |
30 |
24 |
40 |
40 |
70 |
28 |
30 |
70 |
b(мм) |
15 |
12 |
10 |
10 |
16 |
10 |
35 |
20 |
9 |
50 |
№26
№25
№25
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
r(мм) |
10 |
20 |
15 |
20 |
15 |
16 |
15 |
15 |
18 |
12 |
a(мм) |
10 |
15 |
10 |
15 |
10 |
20 |
15 |
10 |
20 |
14 |
b(мм) |
15 |
10 |
10 |
15 |
20 |
15 |
20 |
20 |
10 |
12 |
c(мм) |
20 |
30 |
22 |
24 |
16 |
30 |
20 |
0 |
10 |
0 |
d(рад) |
20 |
16 |
12 |
20 |
12 |
10 |
10 |
20 |
30 |
15 |
№27
|
0 |
1 |
2 |
3 |
4
№28
|
5 |
6 |
7 |
8 |
9 |
r(мм) |
30 |
15 |
21 |
24 |
27 |
20 |
25 |
20 |
20 |
25 |
a(мм) |
100 |
80 |
80 |
90 |
100 |
90 |
100 |
90 |
100 |
70 |
b(мм) |
40 |
30 |
45 |
40 |
40 |
30 |
30 |
25 |
40 |
50 |
c(мм) |
40 |
40 |
40 |
50 |
50 |
70 |
70 |
60 |
40 |
40 |
d(мм) |
100 |
80 |
100 |
100 |
90 |
100 |
110 |
90 |
70 |
100 |
e(мм) |
30 |
30 |
25 |
30 |
50 |
45 |
60 |
30 |
30 |
30 |