3. Центры тяжести простейших тел

1. Прямоугольник (рис. 5)

Ц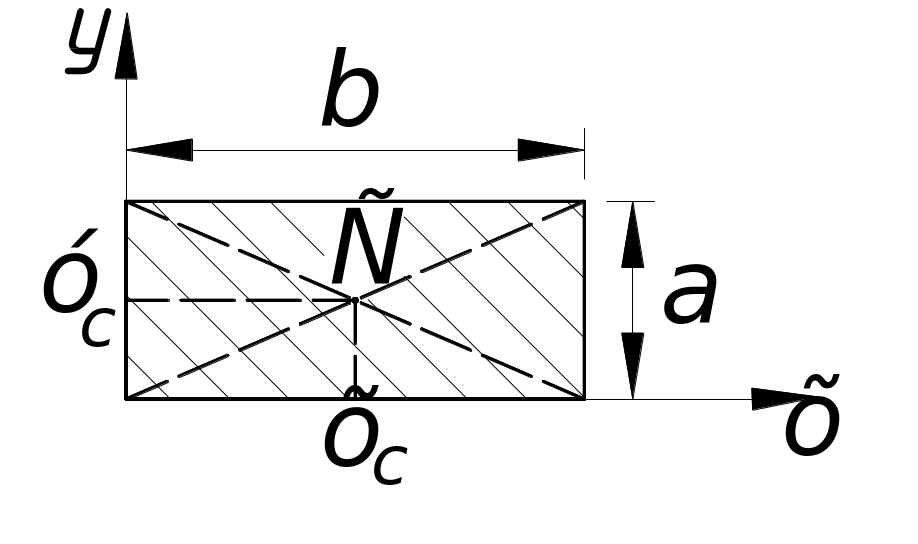 ентр тяжести площади однородного прямоугольника лежит в точке пересечения его диагоналей

.

Рис. 5

2. Т

   Рис. 5

   реугольник (рис.6)

Ц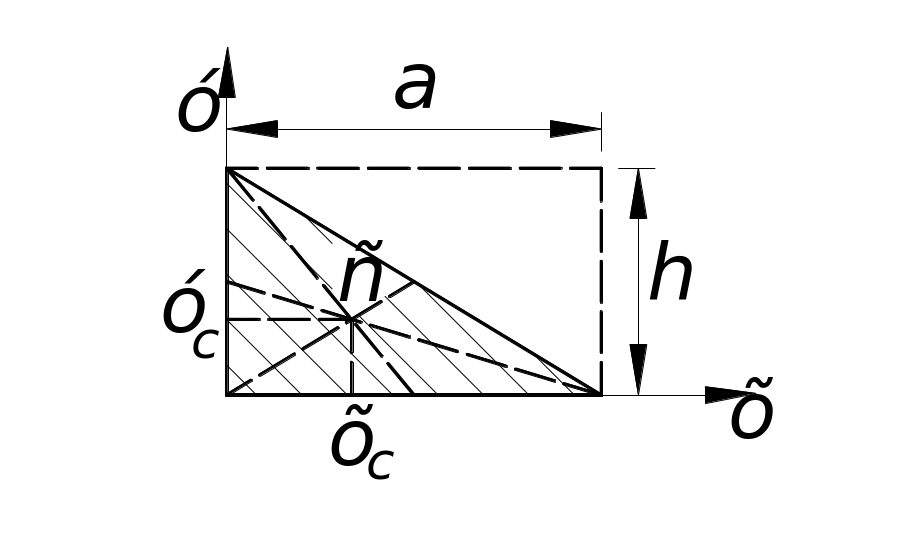 ентр тяжести треугольника находится в точке пересечения медиан

.

Рис. 6

3. Д 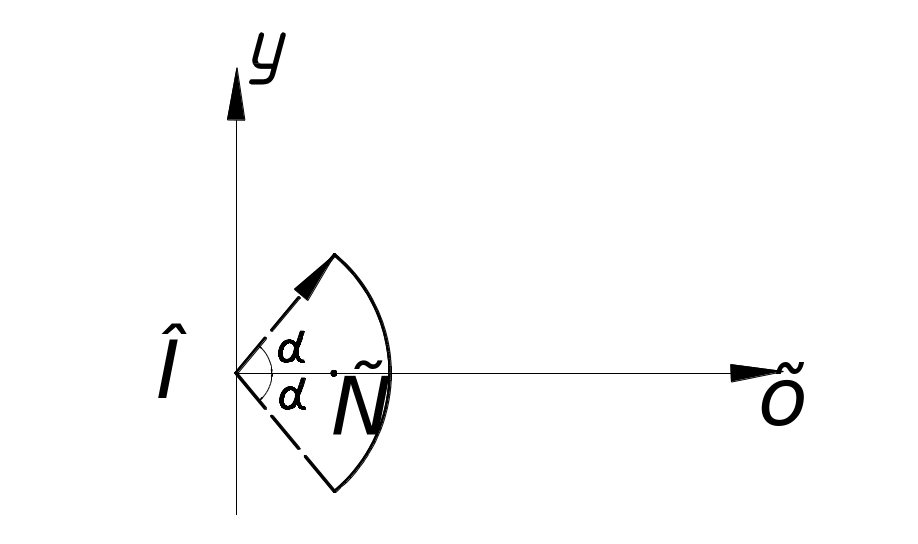уга окружности(рис. 7)

Центр тяжести дуги окружности радиуса с углом при вершине лежит на биссектрисе угла на расстоянии от центра 0,

здесь — измеряется в радианах.

Рис. 7

4. Круговой сектор (рис. 8)

Ц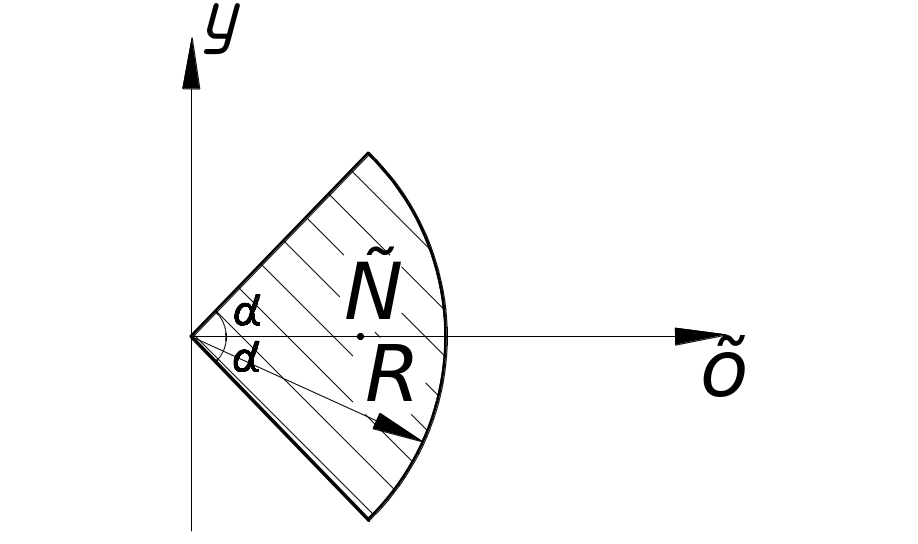 ентр тяжести кругового сектора радиуса с углом при вершине лежит на биссектрисе угла на расстоянии от центра

здесь — измеряется в радианах.

; ;

Рис. 8

.

4. Определение положения центра тяжести фигур

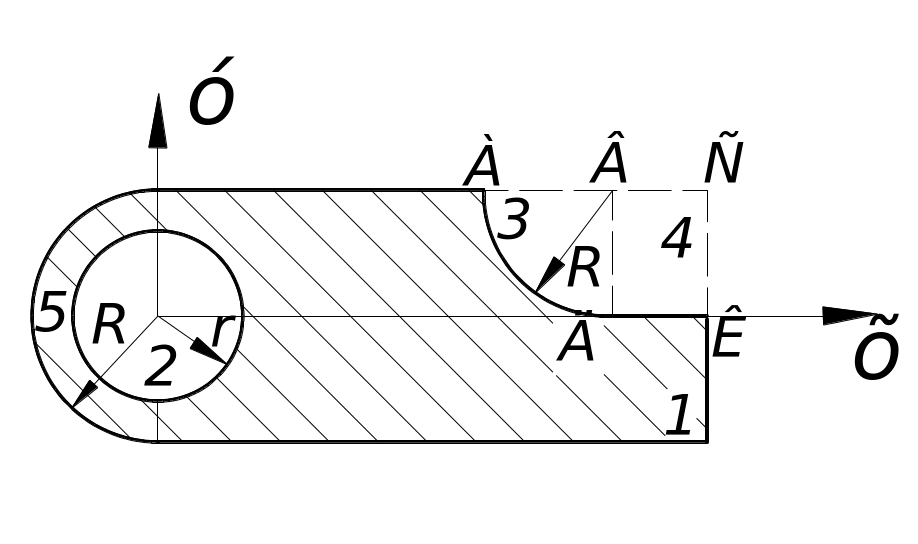
Определить положение центра тяжести однородной пластины, изображенной на рис.9.

r=2 см;

R=4см;

a=6см;

b=2см.

Рис. 9

Решение. Пластина, изображенная на рис. 9, имеет ось симметрии. Вдоль этой оси симметрии проведём ось OX. Из центра окружности малого радиуса перпендикулярно оси OX проведем ось OY. Проведя вспомогательные линии АС, ВД, СК, присоединим к заданной фигуре дополнительно четверть круга 3 и прямоугольника 4. Разобьем полученную фигуру на прямоугольник 1, полукруг 5 и круг 2.

Получили пять фигур, две из которых имеют положительные площади (прямоугольник 1 и полукруг 5) и три — отрицательные (круг 2, четверть круга 3 и прямоугольник 4). В выбранной системе координат OXY координаты центра тяжести заданной фигуры можно определить по формулам

; (17)

.

Рис. 10

Вычислим площади и координаты центров тяжести отдельных фигур, относительно выбранных осей OXY.

1. Прямоугольник(рис. 11)

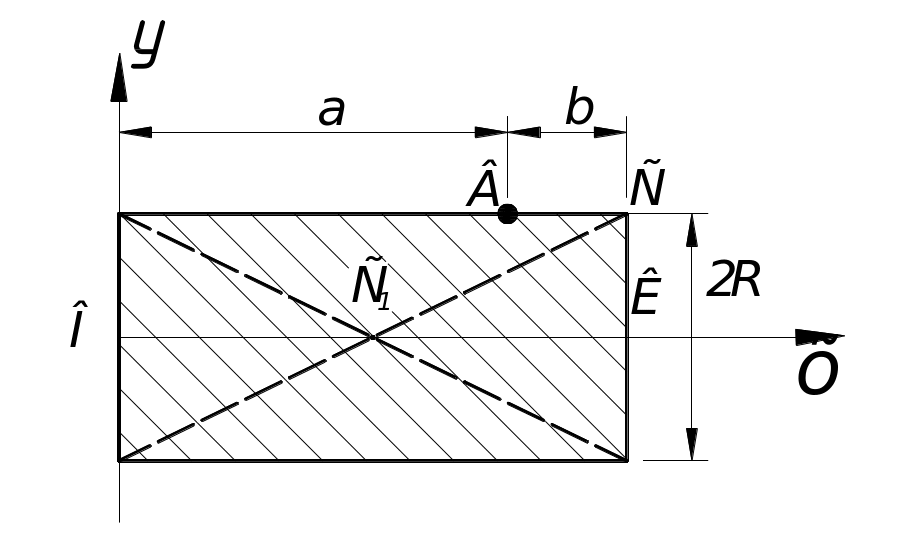
Центр тяжести прямоугольника находятся на пересечении диагоналей. Фигура симметрична относительно оси OX, и, следовательно, центр тяжести фигуры лежит на этой оси, т.е. y₁=0.

; (см).

; (см²).

Рис. 11

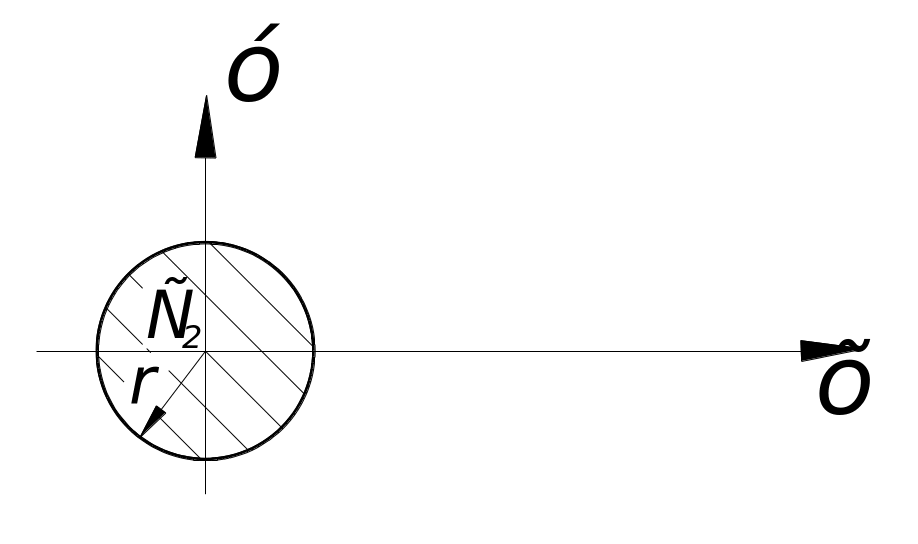2. К руг(рис. 12)

Координаты центра тяжести совпадают с началом координат, таким образом,

; ;

; (см²).

Рис. 12

3. Четверть круга (рис. 13)

Д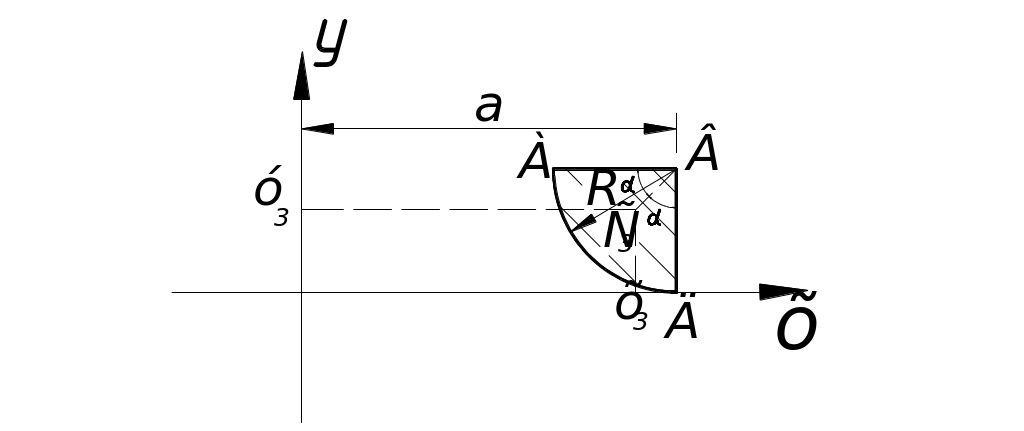 ля кругового сектора отрезок BC, определяется по формуле

.

Р

Рис. 13

ассматриваемый круговой участок представляет четверть круга, и поэтому угол или .

Координаты центра тяжести 3 фигуры в выбранных осях OXY имеют вид

;

;

; (см); (см); (см²).

4. Прямоугольник ДВСК(рис. 14)

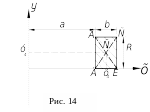
Центр тяжести находится на пересечении диагоналей. Фигура смещена по оси OX вправо на расстояние а.

; ; ;

(см); (см); (см²).

5. Полукруг (рис. 15)

Д ля полукруга отрезок OC₅ определим по формуле

.

Фигура расположена симметрично относительно оси OX, и, следовательно, центр тяжести фигуры находится на этой оси. Таким образом, . Центр тяжести находится левее начала координат, это означает, что координата по оси OX принимает отрицательное значение.

;

(см); (см²).

Подставляем полученные значения в (17) и определяем, что центр тяжести однородного штампа находится в точке, с координатами

(см); (см).