7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

7.1. Первообразная. Неопределённый интеграл. Основные свойства неопределённого интеграла. Основные методы интегрирования

Краткие теоретические сведения

Первообразная

Функция называется первообразной для функции на некотором промежутке , если она дифференцируема на этом промежутке и для всех выполняется равенство .

Теорема 1. Если первообразная для функции на некотором промежутке , то любая другая первообразная для на том же промежутке может представлена в виде , где – произвольная постоянная.

Неопределённый интеграл, его основные свойства.

Если функция первообразная для функции на промежутке , то множество функций , где – произвольная постоянная называется неопределённым интегралом от функции на .

Иначе говоря, неопределённый интеграл от функции – это совокупность всех первообразных . Обозначение:

, (1)

где – подынтегральная функция, – подынтегральное выражение.

Восстановление функции по её производной, или, что то же самое, отыскание неопределённого интеграла по данной подынтегральной функции, называется интегрированием этой функции. Интегрирование представляет собой операцию обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.

Например, т.к. . Аналогично т.к. .

Из определения неопределенного интеграла непосредственно вытекают следующие свойства:

1. Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т.е. .

2. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. .

3. Постоянный множитель можно вынести из под знака интеграла, т.е. если , то .

4. Неопределённый интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций, т.е. .

Непосредственное интегрирование

Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределённых интегралов называется непосредственным интегрированием. То есть непосредственное интегрирование – это сведение данного интеграла к табличному путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла. Ниже приведена таблица интегралов от основных элементарных функций.

Таблица основных интегралов:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12) .

Метод подстановки

Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т.е. перейти к непосредственному интегрированию. Такой подход называется методом подстановки или методом замены переменной.

Теорема 2. Пусть функция определена и дифференцируема на некотором промежутке и пусть – множество значений этой функции, на котором определена функция . Тогда, если на множестве функция имеет первообразную, то на множестве справедлива формула

. (2)

Формула (2) – формула замены переменной в неопределённом интеграле.

Метод интегрирования по частям

Теорема 3. Пусть функции и определены и дифференцируемы на некотором промежутке и пусть функция имеет первообразную на этом промежутке. Тогда на промежутке функция также имеет первообразную и справедлива формула

. (3)

Формула (3) – формула интегрирования по частям в неопределённом интеграле.

Т.к. , то формулу (3) можно переписать в виде

Применять формулу (3) целесообразно, когда интеграл в правой части более прост для нахождения, нежели исходный. Рассмотрим два класса функций , которые целесообразно интегрировать по частям, и укажем, что в этих случаях при представлении подынтегрального выражения в виде произведения следует принять за , а что за . Ниже через обозначен многочлен.

I.

II.

.

Примеры решения типовых задач

Пример 1. Вычислить интеграл .

Решение. Воспользуемся свойствами 3 и 4 и табличными интегралами (5), (2), (3), (9). Получим:

Пример 2. Вычислить интеграл .

Решение. Возведём в квадрат подынтегральную функцию, проведём тригонометрические преобразования, применим свойство 4 и табличные интегралы (2),(5)

Пример 3. Вычислить интеграл .

Решение. Применив тождественные преобразования, свойство 4 и табличные интегралы (2), (10), получим:

Пример 4. Вычислить интеграл .

Решение. Введём переменную , . Тогда Используем формулу (2.1)

.

При замене переменной в неопределённом интеграле иногда более удобно заменять не как функцию , а наоборот, задавать как функцию от .

Пример5. Вычислить интеграл .

Решение. Положим . Тогда . Используя формулу (2.1) и табличный интеграл (3), получим:

.

Пример 6. Вычислить интеграл .

Решение. Применим известное тригонометрическое тождество, далее положим . Тогда . Используя табличный интеграл (2), имеем:

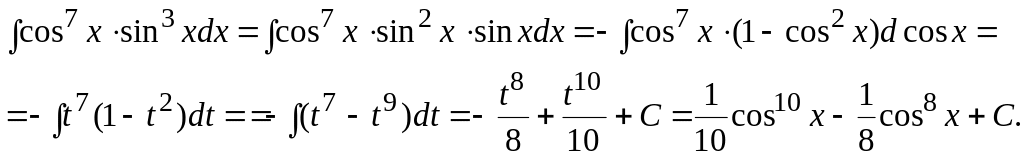Пример 7. Вычислить интеграл .

Решение. Положим . Тогда и по формуле интегрирования по частям получим:

, где .

Пример 8. Вычислить интеграл .

Решение. Положим Тогда и по формуле интегрирования по частям получим:

.

Пример 9. Вычислить интеграл .

Решение. Положим . Тогда и по формуле интегрирования по частям получим:

.

В некоторых случаях формулу интегрирования по частям приходится применять несколько раз.

Пример 10. Вычислить интеграл .

Решение. Положим . Тогда , по формуле интегрирования по частям имеем: . Далее, пусть . Тогда , ещё раз применив формулу интегрирования по частям, имеем:

.