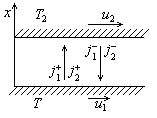- •X. Статистические распределения
- •75. Понятие вероятности
- •76. Свойства вероятности
- •77. Средние значения
- •78. Флуктуации
- •79. Примеры
- •80. Модель идеального газа
- •81. Гипотеза молекулярного хаоса
- •82. Распределение Максвелла. Вывод
- •83. Давление идеального газа. Определение параметра
- •84. Распределение по величине скорости
- •85. Средние скорости и энергия молекул
- •86. Молекулярные пучки
- •87. Ограничения на применимость распределения Максвелла
- •88. Опытная проверка распределения Максвелла
- •89. Распределение Больцмана
- •90. Распределение Гиббса
- •XI. Диэлектрические свойства газов. Теплоемкость идеального газа
- •91. Диэлектрические свойства газов
- •92. Теплоемкость идеального газа
- •93. Чувствительность тепловых приборов и тепловые помехи
- •94. Экспериментальные данные по теплоемкости двухатомных газов
- •95. Теплоемкость газа во внешнем силовом поле
- •96. Теплоемкость квантовых систем
- •XII. Явления переноса в газах
- •97. Введение
- •98. Распределение по скоростям относительного движения
- •99. Частота столкновений и длина свободного пробега молекул
- •100. Распределение по длинам пробега
- •101. Гипотеза локального термодинамического равновесия
- •102. Теплопроводность
- •103. Вязкость
- •104. Диффузия. Закон Фика
- •105. Подвижность частиц. Формула Эйнштейна
- •106. Установление равновесия в ультраразреженном газе
- •107. Перенос тепла и импульса в ультраразреженном газе
- •108. Эффузия
- •Библиографический список
107. Перенос тепла и импульса в ультраразреженном газе
В ультраразреженном газе по-иному протекают и явления переноса. Понятие локального равновесия теряет смысл.
|
Рис. 46 |
![]() .
(107.1)
.
(107.1)
Здесь верхние индексы "+" и "–" означают направление движения, нижние "1" и "2" – номер стенки, в равновесии с которой находятся молекулы. Создаваемый этими молекулами поток тепла равен
![]() .
(107.2)
.
(107.2)
В этом выражении для q учитывается, что молекулы в потоке обладают более высокой средней энергией (на величину kT / 2 каждая).
Потоки молекул удовлетворяют балансовым соотношениям
 (107.3)
(107.3)
Не все эти соотношения являются независимыми – сложение уравнений каждой системы дает j. Из них и определения j следует, что
![]() ,
,
откуда
![]() ,
и с учетом соотношений (107.1) и (107.3)
,
и с учетом соотношений (107.1) и (107.3)
![]() .
В результате
.
В результате
![]() .
(107.4)
.
(107.4)
Поскольку
каждый из потоков
![]() (i = 1, 2) формируется при
отражении от плоской поверхности
практически бесконечных размеров, то
распределение соответствующих молекул
по направлениям движения можно приближенно
считать равномерным. Иными словами, для
связи
с
(i = 1, 2) формируется при
отражении от плоской поверхности
практически бесконечных размеров, то
распределение соответствующих молекул
по направлениям движения можно приближенно
считать равномерным. Иными словами, для
связи
с
![]() можно воспользоваться формулой (86.3):
можно воспользоваться формулой (86.3):
![]() .
(107.5)
.
(107.5)
Здесь деление производится на два (а не на четыре) в связи с тем, что – концентрации молекул, летящих в полусферу. Исключение из соотношений (107.1), (107.3) и (107.5) величин с верхними индексами дает
![]() .
(107.6)
.
(107.6)
С помощью соотношений (107.4), (107.6) выражение (107.2) для q может быть преобразовано к виду
![]() (107.7)
(107.7)
Поток тепла в ультраразреженном газе линейным образом зависит от плотности газа.
Аналогично может быть рассмотрено молекулярное течение между двумя параллельными пластинами, движущихся вдоль самих себя в одном направлении. Для силы трения получается выражение
![]() (107.8)
(107.8)
где S – площадь
пластины. Если температуры пластин
одинаковы и
![]() ( называют коэффициентом
аккомодации), то формула (107.8) упрощается:
( называют коэффициентом
аккомодации), то формула (107.8) упрощается:
![]() (107.9)
(107.9)
|
Рис. 47 |