93. Чувствительность тепловых приборов и тепловые помехи

_{Полученный выше закон равнораспределения энергии по степеням свободы можно применить для оценки точности показаний ряда высокочувствительных приборов. Одним из них является легкое зеркальце, подвешенное на тонкой, обычно кварцевой, нити. Чувствительность прибора определяется возможностью регистрации весьма малых углов поворота зеркальца. Существование предела чувствительности связано с хаотическими колебаниями зеркальца, вызванными тепловым движением молекул зеркальца и нити. При повороте зеркальца на малый угол  оно будет обладать потенциальной энергией u = aφ2 / 2, которая связана с упругими силами нити (a – постоянная, значение которой зависит от радиуса и длины нити, а также от ее материала). Вероятность самопроизвольного поворота зеркальца на тот или иной угол определяется распределением Больцмана. Среднее значение потенциальной энергии равно . Это дает возможность найти среднеквадратичное значение угла поворота зеркальца . При T = 300 K и a = 10 –6 (очень тонкая кварцевая нить) . Эта величина определяет угол, на который поворачивается зеркальце "само по себе". Она же является пределом чувствительности данного прибора.}

Аналогичные результаты могут быть получены для пружинных весов. Флуктуации давления окружающего воздуха и тепловое движение молекул механизма весов приводят к тому, что нагрузка весов хаотически изменяется. Она компенсируется квазиупругой силой χΔx. Потенциальная энергия системы при смещении на Δx равна u = χΔx² / 2. Среднее значение потенциальной энергии по закону равнораспределения составляет . Поэтому среднеквадратичное изменение длины пружины будет . Растяжение пружины грузом m равно Δx = mg / χ. Предельно малая масса, которая может быть найдена при однократном измерении, определяется равенством .

_{Подобным образом может быть установлен предел чувствительности газового термометра, гальванометра и других приборов.}

94. Экспериментальные данные по теплоемкости двухатомных газов

Рис. 40

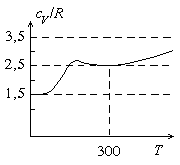
_{В соответствии с законом равнораспределения теплоемкость двухатомных газов должна быть равна 7R / 2. Однако эксперимент показал, что столь большой теплоемкостью двухатомные газы не обладают. Больше того, ее значение зависит от температуры. Эту зависимость теплоемкости можно охарактеризовать следующим образом (рис. 40).}

_{При высоких температурах теплоемкость хотя и не достигает теоретического значения из-за диссоциации молекул, но стремится к нему. При понижении температуры теплоемкость падает и стремится к значению 5R / 2. Это значение достигается при комнатной температуре. При дальнейшем понижении температуры теплоемкость не меняется, пока не начинает сказываться межмолекулярное взаимодействие. Однако для водорода эксперимент обнаружил, что при температурах ниже 80 K теплоемкость становится близкой к 3R / 2.}

_{Выводы теории, хотя и не согласуются с экспериментом, все же не бессмысленны. Водород при очень низких температурах имеет теплоемкость такую же, как и одноатомный газ. Колебательное и вращательное движения молекул водорода по какой-то причине оказываются замороженными. При комнатной температуре, как будет видно из дальнейшего, заморожено колебательное движение. Подобные эффекты наблюдаются и у многоатомных газов.}