§ 13 Параллельное проектирование

До сих пор мы изучали отображения плоскости на себя. В этом параграфе мы познакомимся с параллельным проектированием - отображением плоскости на другую плоскости или пространства на плоскость и установим связь параллельного проектирования с аффинными преобразованиями. Параллельное проектирование применятся при изображении плоских и пространственных фигур на плоскости.

Пусть α – некоторая плоскость и а – прямая, пересекающая эту плоскость. Пусть М – произвольная точка пространства. Через точку М проведём прямую, параллельную прямой а.

Точка М' пересечения этой прямой с плоскостью α называется параллельной проекцией точки М на плоскость α в направлении прямой а.

Проекцией фигуры F на плоскость α в направлении a называется множество проекций всех точек этой фигуры. Если направление проектирования перпендикулярно плоскости проекций, то проекция называется ортогональной.

п.1 .Параллельное проектирование плоскости

Рассмотрим параллельную проекцию плоскости, т.е. случай, когда проектируемая фигура есть плоскость, не параллельная направлению проектирования (если плоскость параллельна направлению проектирования, то её проекция есть прямая).

Очевидна справедливость следующих утверждений:

1. всякая точка плоскости β имеет свою проекцию на плоскость α;

2. всякая точка плоскости α является проекцией некоторой точки плоскости β;

3. если точка М' плоскости α есть проекция точки М плоскости β в направлении прямой а, то точка М есть проекция точки М' на плоскость β в направлении той же прямой.

Таким образом, параллельное проектирование одной плоскости на другую есть взаимно однозначное отображение и обратное отображение также является параллельным проектированием

Рассмотрим некоторые свойства параллельного проектирования плоскости на плоскость.

Теорема 1. При параллельном проектировании плоскости проекцией прямой является прямая, проекцией отрезка – отрезок, проекцией луча – луч; параллельные прямые проектируются на параллельные прямые.

Доказательство этой теоремы предоставляется читателю провести самостоятельно.

Теорема 2. При параллельном проектировании сохраняется отношение отрезков, лежащих на одной прямой или на параллельных прямых.

Доказательство. Проекции отрезков АВ и СD лежащих на плоскости β, обозначим А' В' и C'D'.

Рассмотрим различные случаи их взаимного расположения.

1. Если плоскости α и β параллельны или отрезки АВ и СD параллельны линии пересечении этих плоскостей, то А' В' =АВ и C'D' = СD.

2. Пусть плоскости α и β пересекаются по прямой m и отрезки АВ и СD лежат на прямой, не параллельной m. Тогда отрезки А' В' и C'D' также лежат на прямой, не параллельной m, и прямые А' В' и АВ пересекаются в точке, лежащей на прямой m (рис.23). Прямые AA', BB', CC', DD' параллельны друг другу, и поэтому выполняется равенство

3. Пусть отрезки АВ и СD лежат на прямых, не параллельных m. Требуемы результат нетрудно получить, проведя построение, аналогичное построению, применённому в доказательстве теоремы о сохранении отношения отрезков, лежащих на параллельных прямых, при аффинных преобразованиях.

Теорема 3. Всякий треугольник можно спроектировать в треугольник, подобный любому данному треугольнику.

Доказательство. Пусть ABC и DEF – произвольные треугольники. Плоскость треугольника ABC обозначим β. Через прямую AB проведём произвольную плоскость α, отличную от плоскости β. На плоскости α построим треугольник ABC' , подобный треугольнику DEF . Треугольник ABC' есть параллельная проекция треугольника ABC на плоскость α в направлении прямой СC' (рис.24).

п.2. Параллельное проектирование и аффинные преобразования

Связь параллельного проектирования с аффинными преобразованиями устанавливается следующими двумя теоремами:

Теорема 4. Параллельное проектирование плоскости на плоскость можно представить в виде композиции перспективно-аффинного преобразования и движения.

Доказательство. Пусть р – параллельная проекция плоскости β на плоскость α. Рассмотрим случай, когда эти плоскости пересекаются. Линию их пересечения обозначим m. Существует поворот R вокруг прямой m, отображающей плоскость α на плоскость β. Рассмотрим композицию R·p=. Она есть взаимно однозначное отображение плоскости β на себя, при котором прямые переходят в прямые и сохраняется отношение отрезков, лежащих на одной прямой (поскольку каждое из отображений R и p обладает этими свойствами). Следовательно, композиция  есть аффинное преобразование плоскости β. Все точки прямой при отображении неподвижны. Поэтому  есть перспективно-аффинное преобразование. Таким образом, p = R^-1·.

Пусть теперь плоскости α и β параллельны. Выберем на плоскости произвольную точку А. Очевидно, что p= Т·Е, где Т – параллельный перенос на вектор 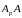, а Е – тождественное отображение плоскости β.

Замечание. Теорема 4 позволяет сводить изучение параллельного проектирования плоскости на плоскость к изучению перспективно-аффинных преобразований, т.е. заменить стереометрическую задачу планиметрической.

Теорема 5. Всякое аффинное преобразование плоскости может быть представлено в виде композиции параллельного проектирования на некоторую плоскость, движения и преобразования подобия.

Доказательство. Пусть  - аффинное преобразование плоскости α. По теореме § 12 оно однозначно определяется заданием двух треугольников Т и Т₁, у которых указаны соответствующие вершины. Пусть  (Т) = Т₁. По теореме 3 настоящего параграфа существует параллельное проектирование p плоскости α на некоторую плоскость β, отображающее треугольник Т на треугольник Т, подобный треугольнику Т₁. Обозначим  движение, переводящее плоскость β в плоскость α (если α и β пересекаются, то  – поворот вокруг линии пересечения; если эти плоскости параллельны, то  - параллельный перенос в направлении проектирования). Треугольник Т при этом переходит в равный ему треугольник Т”(рис.25). Треугольник Т” подобен треугольнику Т₁, поэтому существует преобразование подобия П плоскости α, переводящее треугольник Т” в треугольник Т₁.

Таким образом,

П··р(Т)= Т₁.

Kомпозиция П··р есть аффинное преобразование плоскости. По теореме 6 § 12 оно совпадает с преобразованием .

п.3. Параллельное проектирование пространства

Очевидно, что параллельное проектирование пространства на плоскость не является взаимно однозначным отображением. Проекция прямой, параллельной направлению проектирования, есть точка. Легко видеть, что в остальных случаях проекция прямой есть прямая. Проекцией отрезка является отрезок или точка. Параллельные прямые проектируются в параллельные прямые, одну прямую или в пару точек. Отношение отрезков, лежащих на одной прямой или на параллельных прямых, при параллельном проектировании сохраняется, если их проекции суть отрезки.

Теория изображения пространственных фигур основана на теореме Польке-Шварца. При её формулировке удобно пользоваться понятием четырёхвершинника – плоской фигуры, состоящей из четырёх точек, никакие три из которых не лежат на одной прямой, и соединяющих их отрезков.

Теорема 6. (теорема Польке-Шварца). Всякий тетраэдр можно спроектировать в четырёхвершинник, подобный данному.

Доказательство этой теоремы мы здесь не приводим по причине его громоздскости. С ним можно познакомиться, например, в учебнике А.Л.Вернер, Б.Е.Кантор, С.А.Франгулов. Геометрия т.1. Спецлит, 1997.