2. Расчет свободных (собственных) колебаний

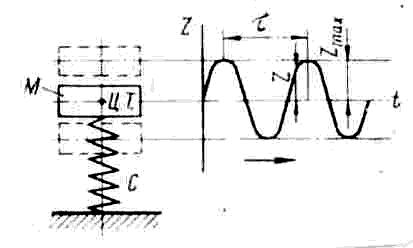
Рис. 7. Схема колебательной системы с одной степенью свободы

Собственные колебания представляют собой гармонические перемещения (или их производные), описываемые в виде синусоиды.

Дифференциальное уравнение свободных колебаний, определяемое силами инерций и упругости системы, имеет вид :

М (1)

Разделив выражение на М, получим

(2)

Обозначим , тогда

(3)

Если тело совершает гармонические колебания с частотой ω и амплитудой Z_мах

Z = Z_мах ·sinωt (4)

то скорость и ускорение могут быть найдены дифференцированием уравнения (4)

=Z_мах ·ω ·cosωt ; _max = Z_мах ·ω ;

=- Z_мах ·ω² ·sinωt ; _max = Z_мах ·ω² ; } (5)

достигают наибольшей величины, когда масса находится в крайних положениях, а величины - в среднем положении.

Свободные затухающие колебания

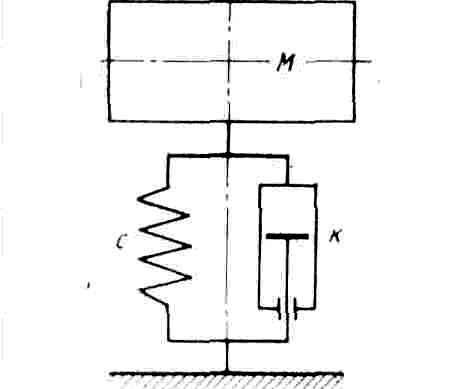
Рис. 8. Схема колебательной системы при наличии демпфера

связаны с закономерностью изменения сопротивления амортизатора.

Сила сопротивления Р_а, создаваемая гидравлическим амортизатором, может изменяться по следующему закону

Р_а = k · , где (6)

k - коэффициент сопротивления амортизатора, кНсм;

- скорость перемещения массы.

В этом случае дифференциальное уравнение колебательного движения запишется в виде

(7)

где 2 h = k /M ; h - коэффициент затухания, с^-1.

Решение уравнения может иметь вид

Z = Z_мах ℓ ^-ht sin

Показатель степени ( - ht ) в уравнении указывает, что колебания будут затухающими. Наличие сопротивления в колебательной системе уменьшает частоту свободных колебаний.

Собственные колебания автомобиля

После проезда неровностей автомобиль на дороге с ровной поверхностью совершает собственные (свободные) колебания.

Частота свободных колебаний существенно влияет на плавность хода автомобиля. С ростом частоты свободных колебаний, как это следует из уравнения (3), ускорение подрессоренных масс автомобиля возрастает, так как .

Действительная колебательная система автомобиля является значительно сложнее рассмотренной одномассовой системы.

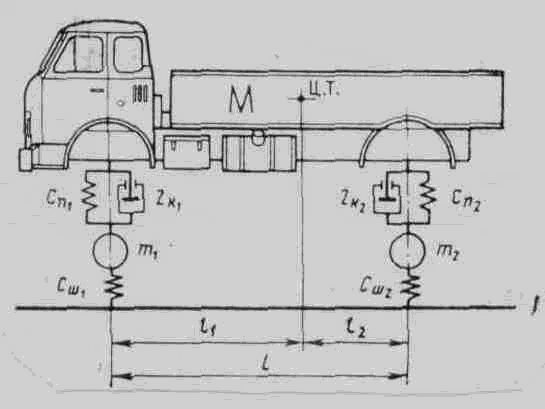
Рис. 9. Схема колебательной системы, эквивалентной двухосному

автомобилю

На рисунке в качестве примера представлена колебательная система, эквивалентная двухосному автомобилю. Эта система включает не только жесткости подвесок С_п1 и С_п2, коэффициенты сопротивления амортизаторов k₁ и k₂ и подрессоренную массу М, но также массу неподрессоренных частей m₁ и m₂, а также жесткости шин передних С_ш1 и задних С_ш2 колес.

Имея эти исходные данные, можно составить дифференциальные уравнения для рассматриваемой колебательной системы, а затем решая их, получить текущие и максимальные значения амплитуд и ускорений свободных колебаний подрессоренных масс автомобиля.

С помощью этих величин можно оценить плавность хода автомобиля.