37. Конечный и бесконечный пределы функции, их геометрическая иллюстрация.
Число А называется
пределом функции f(x) при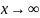 
,
если для любой бесконечно большой
последовательности аргументов функции
(бесконечно большой положительной или
отрицательной), последовательность
значений этой функции сходится к А.
Обозначается
.
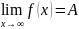предел может быть
равен конкретному действительному
числу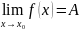 
,
в этом случае говорят, что предел
конечен.
Функция 
не
ограничена сверху. Аналитически свойство
записывается так:
.
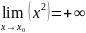Вот и пример геометрического смысла
предела функции: если мы будем уходить
по оси X (влево или
вправо) на бесконечность, то ветки
параболы (значения «игрек») будут
неограниченно уходить вверх на «плюс
бесконечность».
38. Теорема об ограниченности функции, имеющей конечный предел.
Функция называется
ограниченной на X, если
существует такое число K,
что
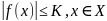
Теорема:
Если функция f(x)
имеет конечный предел при
,
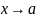то существует проколотая
окрестность в точке А, в которой функция
ограничена.
Доказательство:
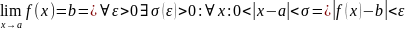
Пусть
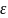- фиксированное число.
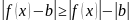
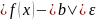
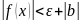
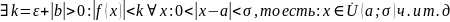
39. Бесконечно малые и бесконечно большие величины, их свойства.
Функция
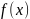называется бесконечно малой при
,
если
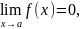то есть б.м.ф. - это функция, предел которой
в данной точке равен нулю.
Функция
называется бесконечно большой при
,
если
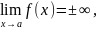то есть б.б.ф. - это функция, предел которой
в данной точке равен бесконечности.
Свойства бесконечно больших и малых:
1) Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
2) Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
3) Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
4) Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
5) Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
40 Основные теоремы о пределах.
1) Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
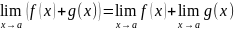
Доказательство.
Проведем доказательство для двух
слагаемых, так как для любого числа
слагаемых оно проводится так же.
Пусть 
.Тогда f(x)=b+α(x) и g(x)=c+β(x),
где α и β –
бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
.
2) Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
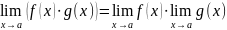
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть
величина постоянная. Функция bβ
+ c α + αβ на
основании свойств бесконечно малых
функций есть величина бесконечно малая.
Поэтому 
.
3) Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
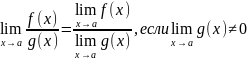
Доказательство.
Пусть 
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α, β –
бесконечно малые. Рассмотрим частное
.
Дробь 
является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
4) Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е.
если
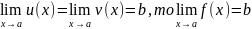
Смысл этой теоремы понятен из рисунка.
5) Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
6) Если две
функции f(x) и g(x) при
всех значениях аргумента x удовлетворяют
неравенству f(x)≥ g(x) и имеют
пределы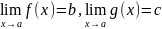 
,
то имеет место неравенство b≥c.
Доказательство: По
условию теоремы f(x)-g(x) ≥0,
следовательно, по теореме 5
