65. Первое достаточное и второе достаточное условие существования экстремума, наибольшее и наименьшее значения функции на отрезке.

Первое достаточное условие экстремума: Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке   непрерывна. Тогда:

• если   при   и   при  , то   - точка максимума;

• если   при   и   при  , то  - точка минимума.

Другими словами:

• если в точке   функция непрерывна и в ней производная меняет знак с плюса на минус, то   - точка максимума;

• если в точке   функция непрерывна и в ней производная меняет знак с минуса на плюс, то  - точка минимума.

Второй достаточный признак экстремума функции: Пусть  ,

• если  , то  - точка минимума;

• если  , то  - точка максимума.

Как видно, этот признак требует существования производной как минимум до второго порядка в точке  .

Наибольшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  .

Наименьшим значением функции y = f(x) на промежутке X называют такое значение  , что для любого   справедливо неравенство  .

66. Выпуклые и вогнутые кривые, достаточное условие выпуклости и вогнутости кривой.

Выпуклость и вогнутость

Свойство графика функции у = f (x) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f (x) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой (рис. 1, а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой (рис. 1, б). Если существуют производные f '(x) и f "(х), то первый случай имеет место при условии, что f "(x) ≥ 0, а второй при f "(x) ≤ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки (рис. 2, a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной (рис. 2, б). Аналогично определяются В. и в. поверхности.

        

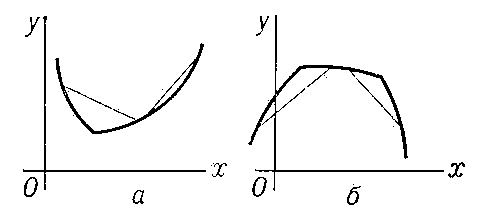
        Рис. 1 к ст. Выпуклость и вогнутость.

        

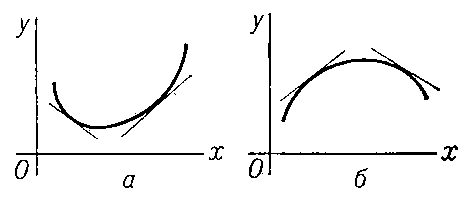
        Рис. 2 к ст. Выпуклость и вогнутость.

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x   ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x   ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

67. Точки перегиба кривой, достаточное условие существование точки перегиба.

Точка   называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.

Первое достаточное условие перегиба графика функции: Пусть функция y = f(x) непрерывна в точке  , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то   является точкой перегиба графика функции.

Второе достаточное условие перегиба графика функции: Если  , а  , тогда   является абсциссой точки перегиба графика функции y= f(x).

Третье достаточное условие перегиба графика функции. Пусть  , а  , тогда если n – четное число, то  является абсциссой точки перегиба графика функции y = f(x).