Добавил:

ICK Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный институт электроники и математики (технический университет)

Предмет:

Уравнения математической физики. Методы математической физики.

Файл:

Конспект лекций по дисциплине Уравнения Математической Физики (УМФ)

.pdf

Скачиваний:

Добавлен:

20.05.2014

Размер:

524.43 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

1)γ – GLADKAQ GIPERPOWERHNOSTX;

2)u0 – GLADKAQ FUNKCIQ, ZADANNAQ NA γ;

3)a(x), b(x), f(x) C(1)(D), γ D Rn, I a(x) = 0, x D;

4)a(x) NE KASAETSQ GIPERPOWERHNOSTI γ NI W ODNOJ TO^KE, T. E. WEKTORY lj = ∂X0 ,

∂ξj

j = 1, . . . , (n − 1), I WEKTOR a x = X0(ξ) LINEJNO NEZAWISIMY:

det ∂ξ1		· · · ∂ξn−1		a X0	(ξ)		= 0,	DLQ L@BOGO ξ I0.
	∂X0		∂X0
tOGDA ALGORITM a2,		W KOTOROM		SLEDUET		SKALQRNYJ		PARAMETR ξ ZAMENITX NA

(n − 1)-MERNYJ WEKTOR-PARAMETR ξ = (ξ1, . . . , ξn−1), A POD x PONIMATX n-MERNYJ WEKTOR x = (x1, x2, . . . , xn), OPREDELQET FUNKCI@ (2.21), QWLQ@]U@SQ ODIN RAZ DIFFERENCIRUEMYM RE[ENIEM ZADA^I (3.1)–(3.2).

3.2kORREKTNOSTX ALGORITMA a1

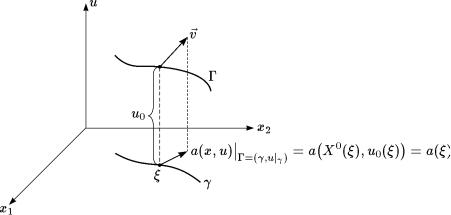
tEOREMA 3.3. pUSTX WYPOLNENY USLOWIQ:

1)γ – GLADKAQ KRIWAQ;

2)u0 – GLADKAQ FUNKCIQ;

3) a1	(x, u), a2(x, u), b(x, u) C(1) D , γ D Rx,u3		I POLNOE WEKTORNOE POLE

v(x, u) = a(x, u), b(x, u) = 0

PRI	(x, u)	D	RIS	. 3.3);
	(x, u)	(		. 3.3);

4)PROEKCIQ HARAKTERISTIK HARAKTERISTI^ESKOJ SISTEMY NA R2x NI W ODNOJ TO^KE NA KRIWOJ γ NE KASAETSQ γ:

	X0	1	(ξ) a1(x, u)	Γ

		2	(ξ) a2(x, u)		= 0	(RIS. 3.3).
det X0		2	(ξ) a2(x, u)	Γ	= 0	(RIS. 3.3).

tOGDA FORMULA (2.11) OPREDELQET ODIN RAZ DIFFERENCIRUEMU@ FUNKCI@ W NEKOTOROJ

OKRESTNOSTI Vδ(γ) = x R2: x = X(ξ, τ), ξ I0, τ Iξ, J(ξ, τ) = 0 .

dOKAZATELXSTWO ANALOGI^NO DOKAZATELXSTWU TEOREMY 3.1.

3.3iNTEGRIROWANIE URAWNENIQ NERAZRYWNOSTI

I URAWNENIJ PERENOSA

3.3.1iNTEGRIROWANIE URAWNENIQ NERAZRYWNOSTI

rASSMOTRIM W TREHMERNOM PROSTRANSTWE TE^ENIE IDEALXNOJ SVIMAEMOJ VIDKOSTI

pUSTX ρ(x, t) –

t. iZ

(BEZ TRENIQ, BEZ ISTO^NIKA I STOKA) S ZADANNYM POLEM SKOROSTEJ v(x, t) C(1)

Rx,t4 .

PLOTNOSTX VIDKOSTI W TO^KE W MOMENT WREMENI

ZAKONA SOHRA

NENIQ MASSY SLEDUET, ^TO FUNKCIQ ρ(x, t) UDOWLETWORQET u~p PERWOGO PORQDKA

∂ρ

(3.3)

+ divx ρ(x, t)v(x, t) = 0,

∂t

KOTOROE NAZYWAETSQ URAWNENIEM NERAZRYWNOSTI.

pOSTAWIM DLQ (3.3) ZADA^U kO[I:

(3.4)

ρ|t=0 = ρ0(x),

pOLXZUQSX

GDE ρ0(x) C(1)

– ZADANNAQ NA^ALXNAQ PLOTNOSTX VIDKOSTI.

FORMULOJ WEKTORNOGO ANALIZA

(3.5)

divx ρv = xρ, v R3 + ρ divx v,

URAWNENIE (3.3) ZAPI[EM W SLEDU@]EM WIDE:

∂ρ

(3.3 )

+ xρ, v(x, t) R3 + ρ divx v(x, t) = 0.

∂t

uRAWNENIE (?? ) PREDSTAWLQET SOBOJ LINEJNOE ODNORODNOE (f = 0) URAWNENIE PERWOGO

PORQDKA (SM. PUNKT 1.2) RAZMERNOSTI n = 4 ((x, t)			R4). gIPERPOWERHNOSTX γ R3	4,
OTWE^A@]AQ NA^ALXNOMU USLOWI@	(3.4),	IMEET WID	γ = (x, t): t = 0, x = ξ, ξ R ,
PRI^EM ρ\|γ = ρ0(ξ).

o^EWIDNO, ^TO W DANNOM PRIMERE WYPOLNENY WSE USLOWIQ TEOREMY 3.2, OBESPE^IWA- @]IE SU]ESTWOWANIE EDINSTWENNOGO GLADKOGO RE[ENIQ ZADA^I (3.3)–(3.4) W NEKOTOROJ

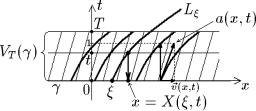
OKRESTNOSTI V (γ) (δ = T ) GIPERPOWERHNOSTI γ (RIS. 3.4). w ^ASTNOSTI, WEKTORNOE POLE

a(x, t) = v(x, t), 1 , a(x, t) R1, OTWE^A@]EE (3.3), TRANSWERSALXNO γ.

pROINTEGRIRUEM ZADA^U (3.3)–(3.4) S POMO]X@ ALGORITMA a2.

1◦. hARAKTERISTI^ESKAQ SISTEMA W RAS[IRENNOM FAZOWOM PROSTRANSTWE Rx,t4									IMEET WID
			dx		x R3,
				= x˙ = v(x, t),
(3.6)			dτ	= x˙ = v(x, t),
		dt		= t˙ = 1.

			dτ
2◦. sOOTWETSTWU@]IE		NA^ALXNYE USLOWIQ DLQ \TOJ SISTEMY						:
2◦. sOOTWETSTWU@]IE								:
(3.7)			x	τ=0 = ξ = (ξ1, ξ2, ξ3)		R3	,
(3.7)		t \|τ=0 = 0.
			\|
oBOZNA^IM RE[ENIE ZADA^I (3.6)–(3.7) NA INTERWALE Iδ = (0, δ), δ > 0 ZA
(3.8)	x = X(ξ, τ),			x, ξ R3,	t = τ,		τ [0, T ];

Lξ – SOOTWETSTWU@]AQ HARAKTERISTIKA, WYHODQ]AQ IZ TO^KI ξ W MOMENT WREME-

NI τ = 0 (RIS. 3.4).

3◦. UDOWLETWORQET SLEDU@]EJ ZADA^E kO[I:							( ) Lξ	= ˜( ) –
pLOTNOSTX SREDY ρ(x, t) W LAGRANVEWYH KOORDINATAH – FUNKCIQ ρ x, t								ρ ξ, τ
								ρ ξ, τ
		dρ˜			v(x, t)		= 0,
(3.9)		\|
(3.9)	dτ (ξ, τ) + ρ˜(ξ, τ) divx					x=X(ξ,τ), t=τ
o^EWIDNO, ^TO				!		"
	ρ˜ τ=0 = ρ0(ξ).			!		"
	RE[ENIE \TOJ ZADA^I IMEET WID
				Rτ	(divx v)\|x=X(ξ,τ ), t=τ dτ
(3.10)				−	(divx v)\|x=X(ξ,τ ), t=τ dτ		.
(3.10)			ρ˜(ξ, τ) = ρ0(ξ)e 0				.

4◦. rAZRE[IM SISTEMU (3.8) OTNOSITELXNO τ I ξ:

τ = t,

ξ = ξ(x, t),

GDE WEKTOR-FUNKCIQ ξ(x, t) = (ξ1, ξ2, ξ3)(x, t) – GLADKOE RE[ENIE SISTEMY URAWNENIJ

(3.11)

xi = Xi(ξ, t),

i = 1, 2, 3.

zDESX X(ξ, t) – PROEKCIQ TO^KI (S KOORDINATOJ t) NA HARAKTERISTIKE Lξ

NA KONFIGU-

RACIONNOE PROSTRANSTWO Rx3

(RIS. 3.4) – ESTX RE[ENIE ZADA^I kO[I

(3.12)

x = v(x, t),

x˙

t=0 = ξ.

wY^ISLIM SOOTWETSTWU@]IJ QKOBIAN:

J(ξ, τ) τ=t

(

= det

∂ξ

∂τ

D(ξ, τ)

τ=t

D X ξ, τ), t(ξ, τ)

∂X(ξ, τ)

∂X(ξ, t)

= det

∂X

(ξ, t) 3 3 = Jx(ξ, t).

∂ξ

∂ξj

I BUDEM S^ITATX, ^TO

(3.13)

Jx(ξ, t) = 0.

(RIS. 3.4) RE[ENIE ZADA^I (3.3)–(3.4) OPREDELQETSQ FORMULOJ

5◦. tOGDA W OKRESTNOSTI VT (γ) =

(x, t)

R4: x = X(ξ, t), t

[0, T ] I Jx(ξ, t) = 0

(3.14)

ρ(x, t) = ρ˜(ξ, τ)

ξ=ξ(x,t), τ=t

= 'ρ0(ξ)e−

0t divx v(x,t)|x=X(ξ,t ) dt (

tEOREMA

pUSTX PRI

3 WYPOLNQETSQ USLOWIE

tOGDA FOR

ξ=ξ(x,t)

3.4.

t [0, T ]

ξ R

(3.13).

MULA (3.14) PREOBRAZUETSQ K SLEDU@]EMU WIDU:

ρ0

(ξ)

(3.15)

ρ(x, t) =

Jx(ξ, t)

ξ=ξ(x,t)

GDE, NAPOMNIM,

(3.16)	Jx(ξ, t) = det	∂X(ξ, t)	= 0,	t [0, T ], ξ R3,

		∂ξ

WEKTOR-FUNKCIQ X(ξ, t) – RE[ENIE ZADA^I kO[I (3.12), A ξ = ξ(x, t) – EDINSTWENNOE GLADKOE RE[ENIE SISTEMY (3.11).

dOKAZATELXSTWO \TOJ TEOREMY OSNOWYWAETSQ NA IZWESTNOJ FORMULE lIUWILLQ.

lEMMA 3.1 (FORMULA lIUWILLQ). qKOBIAN Jx(ξ, t) UDOWLETWORQET URAWNENI@

	d
(3.17)	dtJx(ξ, t) = Jx(ξ, t) divx v(x, t)	x=X(ξ,t).

dOKAZATELXSTWO TEOREMY 3.4. s U^ETOM LEMMY 3.1 IZ FORMULY (3.14) POLU^AEM

ρ(x, t) = 'ρ0(ξ)e−	0	Jx dt (			= ρ0(ξ)e−[ln Jx(ξ,t)−ln Jx(ξ,0)]	ξ=ξ(x,t)	=
	Rt	˙			)	*
		Jx
		Jx
!			"	ξ=ξ(x,t)
!			"
= ρ0(ξ)Jx−1		(ξ, t)
= ρ0(ξ)Jx−1		(ξ, t)

ξ=ξ(x,t)

(ZDESX MY WOSPOLXZOWALISX TEM, ^TO J(ξ, 0) = 1).

dOKAVEM TEPERX FORMULU lIUWILLQ (3.17). dLQ \TOGO NAM PONADOBITSQ SLEDU@]AQ LEMMA.

lEMMA 3.2.

pUSTX x = X(α, t)

–

– PARAMETR) GLADKOE

ODNOPARAMETRI^ESKOE (α

SEMEJSTWO RE[ENIJ SISTEMY URAWNENIJ x˙ = v(x, t),

x R . tOGDA PROIZWODNAQ

∂X(α, t)

= a(α, t) R3

∂α

UDOWLETWORQET LINEJNOJ SISTEME DIFFERENCIALXNYH URAWNENIJ

∂vi

(3.18)

= vx X(α, t), t a(α, t),

∂xj

3 3.

zAME^ANIE. |TA SISTEMA, KAK IZWESTNO [ ], ESTX SISTEMA W WARIACIQH, OTWE^A@]AQ NELINEJNOMU URAWNENI@ x˙ = v(x, t) I EGO RE[ENI@ x = X(α, t).

dOKAZATELXSTWO LEMMY 3.2. pROWEDEM DOKAZATELXSTWO DLQ SLU^AQ n = 1 (x R1). pUSTX x = X(α, t) – ODNOPARAMETRI^ESKOE GLADKOE SEMEJSTWO RE[ENIJ URAWNENIQ

POLU^IM (ISPOLXZUQ TEOREMU `NGA: ∂α∂ dtd = dtd ∂α∂ ) TREBUEMOE RAWENSTWO:

x˙ = v(x, t). tOGDA, DIFFERENCIRUQ PO PARAMETRU α TOVDESTWO

X(α, t) = v X(α, t), t ,

d ∂

∂v

∂X

X(α, t) =

X(α, t), t

(α, t).

∂α

∂x

∂α

dOKAZATELXSTWO LEMMY 3.1. eSLI SU]ESTWUET TREHPARAMETRI^ESKOE GLADKOE SEMEJSTWO

RE[ENIJ SISTEMY x˙ = v(x, t) x = X(α1, α2, α3, t) R3, TO, PRIMENIW (3.18) DLQ KAVDOGO

WEKTORA ai =

∂αi , POLU^IM, ^TO MATRICA RAZMERNOSTI 3 × 3 Y (α, t) =

∂α

∂X

∂X(α, t)

UDOWLETWORQET LINEJNOMU URAWNENI@

(3.19)

Y˙ = vx

X(α, t), t Y.

pOLOVIM TEPERX

α = (α1, α2, α3) = ξ

oBOZNA^IM

J(ξ, t) = det Y (ξ, t),

S^ITAQ

^TO

det Y (ξ, t) = 0,

0 ≤ t ≤ δ (det Y (ξ, 0) = 1), I WOSPOLXZUEMSQ PRAWILOM DIFFERENCIROWA-

NIQ OPREDELITELQ NEWYROVDENNOJ MATRICY:

det Y (ξ, t) = det Y (ξ, t) tr Y˙ Y −1

(ξ, t).

oTS@DA, W SILU (3.19), NAJDEM, ^TO

dJdt = J tr vx X(ξ, t), t Y Y −1 = J tr vx X(ξ, t), t .

dLQ ZAWER[ENIQ DOKAZATELXSTWA OSTAETSQ ZAMETITX, ^TO

×
	∂vi				3	∂vj
tr		3 3	= tr vx
tr	∂xj	3 3	= tr vx	X(ξ, t)	= j=1	∂xj	x(ξ, t), t	= divx v(x, t) x=X(ξ,t).

3.3.2iNTEGRIROWANIE URAWNENIJ PERENOSA

kAK UVE OTME^ALOSX WO WWEDENII, AMPLITUDA KOLEBANIJ POLQ W WOLNOWYH PROCESSAH OPREDELQETSQ W KOROTKOWOLNOWOM PRIBLIVENII IZ TAK NAZYWAEMOGO URAWNENIQ PERENOSA [ , ]. pRIWEDEM ZDESX LI[X DWA WARIANTA \TOGO URAWNENIQ: 1) DLQ AMPLITUDY ϕ(x, t) RE[ENIQ ZADA^I kO[I (W KWAZIKLASSI^ESKOM PRIBLIVENII) DLQ URAWNENIQ {REDINGERA (SM. tETRADI 3 I 4, A TAKVE STR. 50 I ZAME^ANIE NA STR. ??); 2) DLQ AMPLITUDY ψ(x, t) RE[ENIQ ZADA^I kO[I (W KOROTKOWOLNOWOM PRIBLIVENII) DLQ WOLNOWOGO URAWNENIQ (SM. tETRADI 2 I 4).

w PERWOM SLU^AE URAWNENIE PERENOSA IMEET WID
(3.20)	u(x, t), x,tϕ(x, t) + f(x, t)ϕ(x, t) = 0,									x R3, t ≥ 0,
GDE x,t = x,				, u(x, t) =		v(x, t), 1 , PRI^EM ZADANNOE TREHMERNOE WEKTORNOE PO-
GDE x,t = x,			∂t	, u(x, t) =		v(x, t), 1 , PRI^EM ZADANNOE TREHMERNOE WEKTORNOE PO-
LE v(x, t) PRI KAVDOM t R											S(x, t):
			∂
					QWLQETSQ POTENCIALXNYM POLEM S POTENCIALOM
(3.21)							v(x, t) = xS(x, t),
A FUNKCIQ f TAKVE OPREDELQETSQ ^EREZ POTENCIAL S(x, t) PO FORMULE
(3.22)							f(x, t) =	1	∆S(x, t),
(3.22)							f(x, t) =		∆S(x, t),
							2
3	∂2
+
GDE ∆ =	∂x 2	– OPERATOR lAPLASA.
i=1	i

wO WTOROM SLU^AE URAWNENIE PERENOSA DLQ AMPLITUDY ψ(x, t) ZAPISYWAETSQ W WIDE (SM. tETRADX 4)

(3.23)	∂S ∂ψ	− a2(x, t) xS(x, t), xψ(x, t) + f(x, t)ψ(x, t) = 0,				x R3, t ≥ 0,

	∂t ∂t
GDE S(x, t) I a(x, t) – GLADKIE FUNKCII, a(x, t)					> 0, A FUNKCIQ f	TAKVE OPREDELQETSQ
^EREZ S(x, t) PO FORMULE
		1		∂2S	− a2(x, t)∆S .
(3.24)		f(x, t) = aS =
			2	∂t2

pROINTEGRIRUEM URAWNENIE (3.20) PRI USLOWII, ^TO

(C0∞

– PROSTRANSTWO

BESKONE^NO DIFFERENCIRUEMYH FINITNYH FUNKCIJ W Rx S

(3.25) 3

ϕ(x, t) t=0 = ϕ0(x),

ϕ0

C0∞ Rx3 ,

Ω0 = supp ϕ0

KOMPAKTNYM NOSITELEM

oBOZNA^IM ^EREZ

X(x0, t)

RE[ENIE ZADA^I

(3.26)

x = v(x, t),

Ω0,

x˙

t=0

= x0,

I PUSTX QKOBIAN

(3.27)

Jx(x0, t) =

DX(x0

, t)

= 0,

x0 Ω0,

t [0, T ].

Dx0

oBOZNA^IM ^EREZ x0 = x0(x, t) EDINSTWENNOE GLADKOE RE[ENIE SISTEMY

(3.28)

xi = Xi(x0, t),

i = 1, 2, 3,

x0 Ω0,

t [0, T ].

tEOREMA 3.5. pUSTX WYPOLNENO USLOWIE (3.27). tOGDA RE[ENIE ZADA^I (3.20),(3.25) NA OTREZKE [0, T ] OPREDELQETSQ FORMULOJ

(3.29)	ϕ(x, t) =	'		Jx(x0, t)(					.
			ϕ0		(x0)
			,					, ^TO KWADRAT AMPLITUDY KOLE-
dOKAZATELXSTWO SLEDUET IZ TEOREMY 3.4 I TOGO FAKTA								, ^TO KWADRAT AMPLITUDY KOLE-
						x0	=x0		(x,t)

BANIJ ϕ2(x, t) UDOWLETWORQET URAWNENI@ NERAZRYWNOSTI WIDA (3.3) S ZADANNYM POLEM SKOROSTEJ v(x, t), OPREDELQEMYM FORMULOJ (3.21). dEJSTWITELXNO, DLQ FUNKCII ρ(x, t) = ϕ2(x, t) W SILU URAWNENIQ (3.20) I FORMULY WEKTORNOGO ANALIZA (3.5) SLEDUET,

∂ρ

S U^ETOM WIDA f(x, t), ^TO ρ(x, t) UDOWLETWORQET URAWNENI@ ∂t +div ρv = 0, v = xS(x, t). oTS@DA I IZ FORMULY (3.15) SLEDUET UTWERVDENIE TEOREMY.

pROINTEGRIRUEM TEPERX URAWNENIE (3.23) W PREDPOLOVENII, ^TO FUNKCIQ S(x, t) UDOW-

LETWORQET URAWNENI@
	∂S	2
(3.30)		− a2(x, t)( xS)2 = 0.
(3.30)	∂t	− a2(x, t)( xS)2 = 0.

kAK IZWESTNO IZ KURSA OB]EJ FIZIKI, \TO NELINEJNOE u~p PERWOGO PORQDKA ESTX OSNOWNOE DLQ GEOMETRI^ESKOJ OPTIKI URAWNENIE – URAWNENIE \JKONALA (SM. TAKVE PUNKT ??). eGO RE[ENIE S(x, t) OPREDELQET FAZU \LEKTROMAGNITNYH KOLEBANIJ WOLNOWOGO POLQ W KOROTKOWOLNOWOM PRIBLIVENII.

sPOSOBY INTEGRIROWANIQ NELINEJNYH u~p PERWOGO PORQDKA BUDUT RASSMOTRENY NIVE W §4 I §5. zDESX VE MY PREDPOLOVIM, ^TO NAM IZWESTNY DWA GLADKIH RE[ENIQ S±(x, t)

\TOGO URAWNENIQ, KOTORYE UDOWLETWORQ@T URAWNENIQM

	∂S±
(3.31)		± a(x, t)\|xS±\| = 0
	∂t

SOOTWETSTWENNO I, SLEDOWATELXNO, UDOWLETWORQ@T I URAWNENI@ (3.30).

oBOZNA^IM ^EREZ X±(x0, t) RE[ENIE ZADA^I kO[I
	x˙	± = a(x, t)			xS	±	(x, t),
		\|	±
(3.32)			±		xS	±
	x± t=0 = x0,				x0		Ω0	Rx3 ,
A ^EREZ x0 = x0±(x, t) – GLADKOE RE[ENIE SISTEMY
(3.33)				x = X±(x0, t)

OTNOSITELXNO PARAMETRA x0 Ω0.

tEOREMA 3.6. pUSTX WYPOLNENY SLEDU@]IE USLOWIQ:

1) QKOBIAN OTOBRAVENIQ (3.33) OTLI^EN OT NULQ:

Jx±(x0, t) =

DX±(x0, t)

= 0,

x0 Ω0, t [0, T ];

Dx0

2) xS(x, 0) = 0,

x Ω0.

tOGDA FUNKCIQ

ψ(x, t)± = a(x, t)'a(x0, 0) Jx±(x0, t)(

(3.34)

ψ0(x0)

OTREZKE [0, T ]

QWLQETSQ GLADKIM RE[ENIEM URAWNENIQ PERENOSA (3.23) NA

x0=x0±(x,t)

(3.35)

∂S± ∂ψ±

− a2 xS±, xψ±

aS±ψ± = 0

∂t ∂t

I UDOWLETWORQET NA^ALXNOMU USLOWI@

(3.36)

ψ±|t=0 = ψ0(x),

GDE ψ0(x) – PROIZWOLXNAQ GLADKAQ FUNKCIQ.

dOKAZATELXSTWO. pROWEDEM DOKAZATELXSTWO TEOREMY LI[X DLQ SLU^AQ, KOGDA SKOROSTX RASPROSTRANENIQ KOLEBANIJ a(x, t) POSTOQNNA (a(x, t) = a, a = const, a > 0). dEJSTWUEM, SLEDUQ PUNKTAM ALGORITMA a1.

pUSTX x = X±(x0, τ), t = t±(x0, τ) – RE[ENIE HARAKTERISTI^ESKOJ SISTEMY DLQ (3.35)

		dx				dS

(3.37)	dτ± = −a2					dx± (x, t),
	dt±		= dS±		(x, t)

		dτ		dt

S NA^ALXNYMI DANNYMI x(0) = x0 Ω0, t(0) = 0.

nA HARAKTERISTIKE Lx ,τ=0 URAWNENIE (3.35) ESTX OBYKNOWENNOE DIFFERENCIALXNOE URAW-

NENIE PERWOGO PORQDKA OTNOSITELXNO ± ± ± ±

ψ (x0, τ) = ψ X (x0, τ), t (x0, τ) :

(3.38)

± dψ

dτ

	1

(x0, τ) + dψ± ·	2	aS± x	= 0.

iZ LEMMY DLQ 3.1 SISTEMY (3.37) SLEDUET, ^TO QKOBIAN

D X±(x0, τ), t±(x

, τ)

Jx±(x0, τ) =

D(x0, τ)

UDOWLETWORQET URAWNENI@

dEJSTWITELXNO,

= J± aS± X±(x0, τ), t±(x0, τ) .

(3.39)

dτ

− 1/2

−

J±(x0, τ) aS± =

Jx±(x0, τ) −

Jx±(x0

, τ)

−

dτ

−2

dτ

Jx±(x0, τ)

− aS±.

tEPERX PREOBRAZUEM QKOBIAN J±(x0, τ):

D X

±( 0

, τ

)

, t

±(

0, τ)

D X

±(

, τ

)

, t

±(

, τ

)

D(x0, t)

J±(x0, τ) =

D(x0, τ)

D(x0, t)

D(x0, τ)

(3.40)

D X±(x0, τ)

dt±

(x0, τ) = Jx±(x0, t)

(x0, τ).

Dx0

dτ

dt±

dOKAVEM, ^TO PROIZWODNAQ

(x0, τ) POSTOQNNA WDOLX TRAEKTORIJ SISTEMY (3.37). w SA-

dτ

MOM DELE, W SILU (3.37) I URAWNENIQ (3.31) IMEEM

dτ±

(x0, τ) =

∂t± x=x±(x0,τ), = xS

X±(x0, τ), t±(x0, τ) = P ±(x0, τ) .

∂S

wY^ISLIM TEPERX

t=t±(x0,τ)

∂

∂S± ∂t±

P ±(x0, τ) =

xS± X±(x0, τ), t±(x0, τ) = x xS±,

∂τ

dτ

∂t

∂τ

oTS@DA, W SILU SISTEMY (3.37), NAJDEM, ^TO

∂τ P ±(x0, τ) = x xS±, −a2 xS±

∂t±

∂

∂S

= x

∂t± − a2 xS± 2 X±(x0, τ), t±(x0, τ) = 0.

∂S

MAS[TAB WRE-

pOSKOLXKU FUNKCII S±(x, t) UDOWLETWORQ@T URAWNEI@ \JKONALA (3.30): aS± = 0. tAKIM OBRAZOM, IZMENIW NA FIKSIROWANNOJ TRAEKTORII SISTEMY (3.37)

	dt±
NAJDEM, ^TO FUNKCIQ

MENI τ → t S U^ETOM FORMULY	dτ	(x0, τ) =			P ±(x0)		= 0 IZ FORMUL (3.39) I (3.40)
ψ±(x, t) = '				Jx±(x0, t)(			,
			ψ0(x0)
			,

						x0=x0±(x,t)

GDE ψ0(x) — PROIZWOLXNAQ GLADKAQ FUNKCIQ, QWLQETSQ RE[ENIEM URAWNENIQ

PERENOSA (3.35). dLQ ZAWER[ENIQ DOKAZATELXSTWA OSTAETSQ ZAMETITX, ^TO PRI ZAMENE PARAMETRA τ NA t (t = t±(x0, τ)) FUNKCIQ X± x0, τ±(x0, t) = X±(x0, t) ESTX RE[ENIE

SISTEMY (3.33).

uPRAVNENIE. dOKAVITE FORMULU (3.35) DLQ OB]EGO SLU^AQ (a(x, t) = 0).

pRIMER. rASSMOTRIM TEPERX ODNOMERNU@ PO x WERSI@ URAWNENIQ PERENOSA (3.23) W STACIONARNOJ NEODNORODNOJ SREDE, (T. E. W TAKOJ SREDE, W KOTOROJ SKOROSTX RASPROSTRANENIQ KOLEBANIJ a(x, t) NE ZAWISIT OT WREMENI t I QWLQETSQ GLADKOJ FUNKCIEJ x: a(x, t) ≡ a(x) > 0)

(3.41)	∂S± ∂ψ±	− a2(x)	∂S± ∂ψ±	+	1	aS±ψ± = 0.

	∂t ∂t		∂x ∂x		2

zDESX FUNKCII S±(x, t) ESTX GLADKIE RE[ENIQ URAWNENIQ LINEJNOJ BEGU]EJ WOLNY W NEODNORODNOJ SREDE SO SKOROSTX@ ±a(x) SOOTWETSTWENNO

(3.42)

∂S±

± a(x)

∂S±

= 0.

∂t

∂x

oBOZNA^IM ^EREZ X(x0, t) RE[ENIE ZADA^I kO[I

(3.43)

x˙ = a(x),

t=0 = x0

(KOTOROE, O^EWIDNO, LEGKO NAHODITSQ W KWADRATURAH). tOGDA OB]EE RE[ENIE URAWNENIQ

PERENOSA ( ) ZADAETSQ FORMULOJ

(3.44)

ψ±(x, t) = ψ0

a(x)

X(x, t) -a X(x,

GDE ψ0(x) – PROIZWOLXNAQ GLADKAQ FUNKCIQ.

uPRAVNENIE. dOKAVITE FORMULU (3.44).

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете Уравнения математической физики. Методы математической физики.

#
20.05.2014524.43 Кб66Конспект лекций по дисциплине Уравнения Математической Физики (УМФ) .pdf
#
20.05.20142.41 Mб116Лекции по дисциплине Уравнения Математической Физики.doc