
- •1. Основные законы газодинамики
- •1.1. Характеристики потока жидкости
- •1.2. Параметры потока. Уравнения состояния
- •1.3. Закон сохранения энергии в потоке жидкости
- •1.4. Параметры заторможенного потока
- •1.5. Располагаемая энергия, скорость потока
- •1.6. Уравнения неразрывности и расхода
- •1.7. Закон импульса сил в потоке жидкости
- •2. Уравнения параметров потока
- •2.1. Скорость звука. Число м
- •2.2. Зависимость профиля канала от скорости
- •2.3. Уравнения параметров потока идеального газа
- •2.4. Критический режим течения. Число
- •2.5. Уравнения параметров потока идеального газа
- •2.6. Основные газодинамические функции
- •2.6.1. Г.Д.Ф. Скорости
- •2.6.2. Г.Д.Ф. Параметров термодинамического
- •2.6.3. Г.Д.Ф. Плотности потока массы ( расхода)
- •2.6.4. Г.Д.Ф. Импульса потока газа
- •2.7. Уравнения состояния, расхода и импульса сил в г.Д.Ф.
- •2.8. Изменение параметров вдоль оси канала
- •3. Основные закономерности сверхзвукового потока газа
- •3.1. Распространение в потоке газа слабых возмущений
- •3.2. Конечное расширение газа в сверхзвуковом потоке
- •3.3. Конечное сжатие сверхзвукового потока
- •3.4. Свойства скачков уплотнения
- •3.5. Основные уравнения прямого скачка уплотнения
- •3.6. Параметры потока газа за прямым скачком уплотнения
- •3.7 Косой скачок уплотнения
- •3.8. Угол наклона косого скачка
- •3.9. Отклонение потока за косым скачком уплотнения
- •3.10. Процессы в сверхзвуковом канале на
- •II группа режимов - или
- •III группа режимов или
- •IV группа режимов .
- •3.11. Расход газа через каналы на переменных
- •3.11.1. Расход несжимаемых сред
- •3.11.2. Расход сжимаемых сред через суживающиеся каналы
- •3.11.3. Расход газа через расширяющиеся каналы
2.6.3. Г.Д.Ф. Плотности потока массы ( расхода)
Основной функцией этой группы является
приведённая плотность потока массы,
т.е. отношение
![]() в рассматриваемом сечении к
в критическом сечении потока.
в рассматриваемом сечении к
в критическом сечении потока.
 .
(2.11)
.
(2.11)
Плотность потока массы в соответствии с уравнением (1.14) равна
![]()
следовательно при одинаковых расходах во всех сечениях потока – все остальные случаи это предмет газодинамики потока переменной массы – рассматриваемая г.д.ф. равна
![]() (2.11.1)
(2.11.1)
т.е. является функцией площади потока; в этом особая ценность этой функции, т.к. она по существу связывает параметры потока с конструктивным параметром канала.
Для потоков с круговым сечением введена формальная газодинамическая функция
![]() . (2.11.2)
. (2.11.2)
Другая формальная газодинамическая функция
 (2.12)
(2.12)
введена, как будет показано ниже, с целью иметь уравнение расхода, выраженное через статическое давление и г.д.ф.
Зависимости расходных г.д.ф. от , так принято называть г.д.ф. этой группы, показаны на рис. 2.1, а их критические и граничные значения в табл. 2.1.
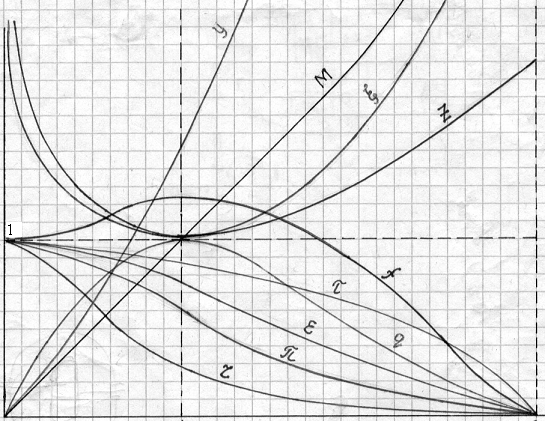 λ
λ
0 1
![]()
Рис.2.1. Зависимости газодинамических функций от λ.
2.6.4. Г.Д.Ф. Импульса потока газа
При рассмотрении в параграфе 1.7 закона импульса сил в потоке газа и его приложения к техническим задачам были даны понятия полного импульса потока, статического импульса потока, плотности полного импульса потока. Г.д.ф. импульса являются их относительными величинами, предназначены для описания силового воздействия, потока и в частности используются в расчётах реактивных двигателей.
Приведённый полный импульс потока – отношение полных импульсов потока в рассматриваемом и критическом сечениях
![]() .
.
Данная г.д.ф. не зависит от показателя k.
Относительный статический импульс – отношение статического импульса к полному импульсу потока в рассматриваемом сечении
![]() .
.
Относительная плотность полного импульса потока – отношение плотности полного импульса потока к давлению заторможенного потока в том же сечении
 .
.
Зависимости г.д.ф. импульса от показаны на рис. 2.1, их граничные и критические значения приведены в табл. 2.1.
2.7. Уравнения состояния, расхода и импульса сил в г.Д.Ф.
Записав уравнения параметров состояния для статических и заторможенных параметров, после деления их друг на друга, получаем уравнение состояния параметров газа, выраженное в г.д.ф.
![]() ,
,
,
,
![]() (2.13)
(2.13)
Связь расхода с г.д.ф. можно получить домножив и разделив уравнение расхода (1.14)
на произведение
![]() .
Учитывая, что
.
Учитывая, что
![]() и заменяя
,
формулами (2.5.3), (2.6), получаем
и заменяя
,
формулами (2.5.3), (2.6), получаем
 (2.14)
(2.14)
где
![]() - комплекс, характеризующий физические
свойства газа, определяемый формулой
(2.6.2)
- комплекс, характеризующий физические
свойства газа, определяемый формулой
(2.6.2)
Домножив уравнение (2.14) на
![]() ,
получаем
,
получаем
 (2.14.1)
(2.14.1)
Приравнивая уравнения (2.14) и (2.14.2) для двух сечений, находим уравнение неразрывности, представленное в газодинамических функциях
![]() и
и
![]() .
(2.15)
.
(2.15)
В газодинамических выкладках и расчетах удобно использовать уравнение импульса не в явном виде, а выраженным через полный импульс
![]() .
.
Преобразования произведения расхода на критическую скорость

![]()
приводят уравнение полного импульса к виду
![]() (2.16)
(2.16)
