1.3. Закон сохранения энергии в потоке жидкости
Закон сохранения энергии или первое начало (закон) термодинамики в общем случае имеет вид
,
(1.4)
где Q – подведённое (отведённое) к телу тепло извне,
- тепло, выделенное телом в результате
работы сил трения
,
L – работа, подведённая (отведённая) к телу извне,
z – потенциальная энергия тела.
Для технических систем z
– мала и изменение dz
ничтожно,
.
Поток жидкости является энергоизолированной
системой, в которой dQ
= 0, dL = 0,
и закон сохранения энергии для потока
жидкости произвольного типа принимает
вид
(1.4.1)
(1.4.2)
Уравнение энергии (1.4.2) показывает, что изменение скорости потока жидкости (сжимаемой, несжимаемой, реальной, идеальной) можно получить только за счёт изменения его энтальпии.
В общем случае
,
для энергоизолированной системы dQ = 0, тогда уравнению энергии (1.4.1) можно придать вид
(1.4.3)
Для несжимаемой жидкости интегрирование уравнения (1.4.3) придаёт закону сохранения энергии следующий вид
(1.4.4)
По имени учёного члена Российской академии наук, впервые получившего это уравнение в 1738 г., его называют уравнением Бернулли.
1.4. Параметры заторможенного потока
Постоянная
как видно из уравнения (1.4.2) является
энтальпией жидкости при
.
Если существует
обязаны быть
,
,
,
- их называют параметрами заторможенного
потока. Это реально существующие
величины, которые могут быть измерены.
Если открытый вход трубки (рис.1.3)
разместить параллельно вектору скорости
набегающего потока жидкости, то
измерительные приборы покажут статические
(термодинамические) значения давления
или темперартуры p,
T ; при размещении
входа трубки перпендикулярно вектору
скорости – приборы дадут значение
параметров заторможенного потока
,
.
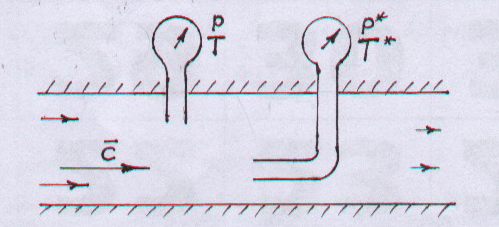
Рис 1.3. К заторможенным параметрам.
Заменяя в уравнении (1.4.2) энтальпии
зависимостью (1.1) и разделив его на
(1.1.1), получаем формулу для определения
температуры заторможенного потока
идеального газа
.
(1.5)
Допуская процесс торможения изоэнтропийным, с помощью уравнений (1.3.1), (1.3.2) получаем зависимости для определения давления, плотности и удельного объёма заторможенного потока
Формула для определения давления заторможенного потока несжимаемой жидкости следует из уравнения (1.4.4)
(1.8)
Параметры торможения реального потока из-за теплообмена и вязкости жидкости отличаются от рассчитанных по формулам (1.5) – (1.8). Их расчет производится по тем же формулам, но вводом в них эмпирических коэффициентов.