Соотношения неопред. Гейзенберга

В силу наличия волновых свойств у микрочастицы однозначная связь между координатой и импульсом нарушается.

Из соотн. следует, что для микрочастич одновременно с одинаковой точностью местоположение объекта и импульс определены быть не могут. Это говорит о наличии влновых свойств.

Для энергии:

Произведение неопределённости энергии микрочастицы на длительность пребывания этой частицы в этом состоянии не может быть меньше постоянной Планка. уровней энергии нет. Ур-ние Шредингера для частицы в ящике и его решение.

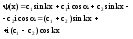
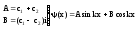
Тригонометрическая форма ур-ня Шред. Ур-ние Шредингера для барьера бесконечной ширины. I область:

;

Решение: \II область:

14.Ур-ние Шред. для стацион. состояния. Понятие о стационарных состояниях.1) Потенциальная силовая ф-ция для микрочастицы от времени не зависит: U(x,t)=U(x)=const В этом случае U(x) - потенциальная энергия микрочастицы. 2)-ф-ция должна со временем не меняться: ||² = const по времени. 3) Полная энергия остаётся постоянной: E=const по времени. 4) Для стационарных состояний волновая -ф-ция распадается на 2 сомножителя: (x,t)=(t)·(x). (t) - временной множитель; (x) - координатная часть истинно волновой ф-ции. Стационарное ур-е Шредингера Для нахождения (x,y,z) из (2) и (2’) необходимо составить ур-ние без времени. Сделаем переход от (2), испольуя возможность замены (x,t) на (t) и (x).

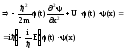
... (1)

стационарное уравнение Шредингера. E - полная энергия; U(x) - потенциальная энергия, m - масса.  - ?. ... (1’) - Для одномерного случая. EU=T.

(x,y,z), U(x,y,z)   - оператор Лапласса. Физич. смысл решения стацион. ур-ния Для нахождения (x) надо решить (1). Ур-ние (1) решается при след. условиях: 1) Известна U(x). ;2) Должны быть известны граничные условия для координат частиц, т.е. известны(0) и (). 3) (x) - непрерывна, однозначна, конечна. 4) Решение (1) возможно только при опред. дискретных значениях E₁, E₂,...,E_n. Каждому значению энергии соотв. своя -функция ₁, ₂,...,_n. Каждая из -функций должна удовлетворять условию нормировки: , n=1,2,3, ..., m Каждая-функция описывает независимое от соседнего состояние:

- независимость, ортогональность

- помнож. на комплексно-сопряжённое.

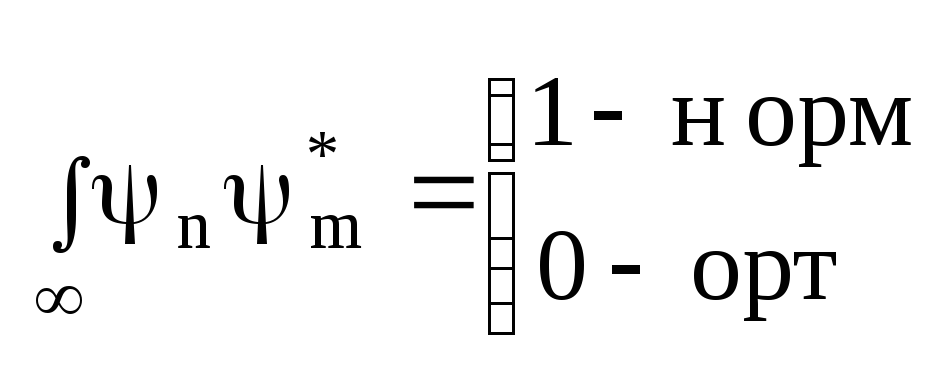- условие ортонормировки.

15.

Ур-ние Шредингера для частицы в ящике и его решение.

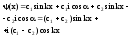
16.

2) Метод для сильной связи (E<U, диэлектрики). Для диэл-ков решение приводит к рассмотрению туннельного эффекта.

Для сильной связи движение эл-на не свободное. Электрон находится около своего ядра ~10^-15 сек, а далее он туннелирует к соседнему ядру. Там он находися тоже ~10^-15 сек и туннелирует к соседнему ядру. И т.д., т.е. движение эл-на эстафетное, с остановкой у ядер других атомов. У удалённых от ядра электронов вероятность туннелирования больше.

За счёт туннельного эффекта и с учётом соотношений неопределённости разрешимыми значениями энергии являются зоны. Запишем соотношения неопределённости:

;c

Дж ~ 1 э.В.

Билет 15

Применение квантовой механики: движ-е свобод. МЧ.

Свободным назыв-ся движ-е частицы, при котором на неё не дейст-т никикие внеш. силы.

U(x)=0

δ²Ψ/ δx² + (2m/ħ²)E Ψ=0

k²=2mE/ ħ² => k=√2mE/ ħ²

δ²Ψ/ δx² + k²Ψ=0

Ψ=e^rx δ²Ψ/ δx²=r²Ψ

r²+k²=0 – характеристич. ур-е

r_1,2= ±ik

Ψ1=C1e^ikx

Ψ2=C2e^-ikx

Ψ (x)=C1e^ikx+C2e^ikx

Если рассм. движ-е МЧ. в каком-то из напр-й, то досстаточно взять одно из частн. реш-й.

Для того, чтобы найти С1 необх. нормир-ть функ-ю на 1. В дан. случае интегралнормир-ки расход., т.к. интегриров-е произв-ся по бесконеч.пространству, поэтому сначала провод нормир-ку предполож-ем, что Ψ-периодич. ф-я с периодом T.

Ψ(x)= Ψ(x+L)

C1e^ikx= C1e^ik(x+L)

e^ikL=1 – ф-ла Эйлера

cos(kL)=1

kL=2πn => k=2πn/L

_-L/2∫^L/2 |Ψ|²dx =1

Ψ(x)= C1e^ikx

_-L/2∫^L/2 C1²dx =1

C1² L=1 => C1=1/√L

Ψ(x)= (1/√L) e^i2πkx/L

E= k²ħ²/2m => E=2π²n²ħ²/mL²

Для свободн. прост-ва L->∞

ΔE = 4π²nΔnħ²/mL² - разность меж. возм-ми энергиями частицы.

n=0,1,2....

Δn=1

p=ħk = 2πnħ/L

ΔE=2πħp/mL

Т.к. v имеет непр-й ряд значений, то и энерг. частицы имеет непр. р. знач. при L->∞ и

ΔE->0, при этом k²>0 (если k²<0, то энергия отриц., что не имеет знач-я для своб. МЧ)

Ψ(x,t)=e^iEt/ħ Ψ(x)

Ψ(x,t)= (1/√L) e^i(Et-px)/ħ

Билет 16

МЧ в одномерной прямоуг-й потенц-й яме с беск-но выс. сиенками.

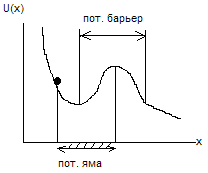
В классич. физике частица, вывед-я из полож-я равновес. занимает сост-е с наименьш. потенц. энергией. Для того, чтобы преодолетьпотенц. батьер, его энергия д.б. больше потенц-й.

Для част., наход-ся внутри пот-й ямы,эта конфигурация поля зап-ся в виде:

U(x)={0, 0≤x≤l

{Uo, x>l,x≤0

U(x)={0, 0≤x≤l

{∞, x>l,x<0

Потенц. ящик = пот. яма.

Рассм. 3-й случай: вся область простр-ва разбив-ся на 3 обл.

1 и 3 обл. – част. в них попасть не может.

2 обл. – част. нах-ся в ней и ее пот. энерг. = 0

δ²Ψ/ δx² + (2m/ħ²)[E-U(x)] Ψ=0

Граничн. условия:

Ψ(0)=0 , Ψ(l)=0

Ψ"/ Ψ = -(2m/ħ²)[E-U(x)]

На гран-х обл. энерг. частицы -> ∞

E ->∞ Ψ->0

2 обл U(x)=0

δ²Ψ/ δx² + (2m/ħ²)E Ψ=0

Решение этого ур-я м. представ. в виде экспаненты, с пом. ф-лы Эйлера.

Ψ (x)=A sin(kx+α)

k, α - ?

они находятся из начальных усл.

x=0 => Ψ(x)=0

Asin α=0 , α=0

l=0 => Ψ(l)=0

Asin(kl)=0 , kl=πn , n=1,2...

k= πn/l

k²=2mE/ ħ² => E= k²ħ²/2m => E=2π²n²ħ²/mL²

Энергия МЧ имеет дискр. спектр знач-й.

Для нахожд-я нормирующ. множителя A, возьмем интеграл.

₀∫^l |Ψ|²dx =1 (усл. нормир.)

Ψ(x)=A

₀∫^l A²sin²( πnx/l)dx =1

₀∫^α A sinα dα = α/2 - sin2α/4

l/πn ∫ sin²( πnx/l)[dx(πn/l)] = l/πn ₀∫^πn sin²α dα

x=0

α = πnx/l α=0

x=l , α=πn

l/πn ₀∫^πn sin²α dα = l/πn [πn/2 – 0 – (0)*1/4 ] = l/2

l/2*A² =1 => A=√2/l

Ψ(x)= √2/l * sin( πnx/l) – опис. сост. МЧ в ящике

E=2π²n²ħ²/ml²

Анализ сост-я МЧ в пот. ящике

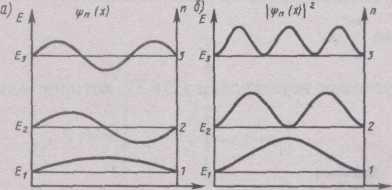
E=2π²n²ħ²/ml²

n=1 E=2π²n²ħ²/ml²

x=0 Ψ=0

x=l Ψ=0

x=l/2 Ψ=

Ψ(x)= √2/l * sin( πx/l)

n=1 |Ψ(x)|² = 2/l * sin² ( πx/l)

n=2 E₂ = E=4π²ħ²/2ml² = 4Eo

Сост-е с n=1 – назыв-ся основным; сост-е с n>1 назыв. возбужд-м.

x=0 Ψ=0

x=l Ψ=0

x=l/2 Ψ=0

x=l/4; 3*l/4 Ψ-> max

Ψ(x)= √2/l * sin( 2πx/l)

n=2 |Ψ(x)|² = 2/l * sin² (2πx/l)

C увел-ем энерг. МЧ увелич-ся число мест, в кот. вероятн. найти эту част. одинакова .

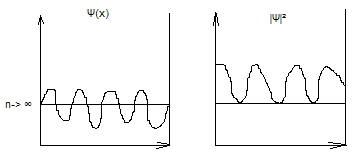
При n-> ∞ повед-е част. стремится к повед-ю классич. част.

Как отл. класс. част. от квантовой?

Для этого посчит. разность энергий сосед. уровней (n+1) и n.

ΔE=E_n+1 + En = [ (n+1)² - n² ] π²ħ²/2ml²

ΔE = (2n+1)π²ħ²/2ml²

Для молекулы газа , нах-ся в объеме размером l=10см.

ΔE= 10^-20n эВ

(m≈10^-23 г , l=10см)- это классич. част.

Если мы возьмем свободн. эл-н в куске металла.

ΔE= 10²n эВ

(m≈10^-30 г , l=10 см)

Если электрон в атоме:

ΔE= 10²n эВ

(m≈10^-30 г , l=10^-10 м)

В пределе n-> ∞ любое полож-е частицы станов-ся равновероятн.

1) Энерг. част. в пот. яме имеет дискр. спектр знач.

2) Т.к. n≠0 (иначе Ψ_ф=0) то мин. энерг. МЧ ≠0

3)При увел-и массы част-цы она м. рассм-ся , как классич, т.к. ΔE->0

4) При n-> ∞ увелич-ся число максимумов |Ψ|² , т.е. вероятн. найти МЧ в любом месте ящика станов-ся одинаковой (классич. част.).

17-18

Прохождение частицы через потенциальный барьер бесконечной длинны

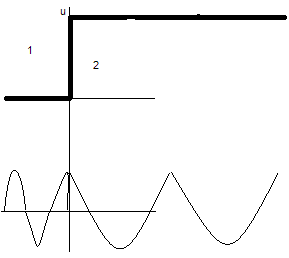
1 обл.

U(x) = 0 ( X>0)

²/x² +(2mE/ ħ²)  = 0

Решение

(x) = A₁e^ik1x + B₁e^-ik1x

k₁² = 2mE/ ħ²

Это решение представляет собой совокупность двух волн, распр. В противоположных направлениях. Первое слагаемое в положит. направлении оси Х(падающая волна), Второе слагаемое в отриц. Направлении (отражённая волна).

Волна де Бройля получается при домножении на временной множитель.

2 обл.

U(x) = U₀ (X>=0)

²/x² +(2mE/ ħ²)[E – U₀]  = 0

Решение

(x) = A₂e^ik2x + B₂e^-ik2x

k₂² = (2m/ ħ²)[E – U₀]

Это решение образовано только волной прошедшей через барьер, т.е. В области 2 отражённой волны не существует. Поэтому B₂e^-ik2x = 0.

1 случай E>U₀

k1 = 2/1; k2 = 2/2 => k1>k2, 1>2

Длинна волны де Бройля после входа в барьер увеличивается

2 случай E< U₀

k2 = ((2m/ ħ²)[E – U₀]) =  (-(2m/ ħ²)[E – U₀]) = ik’

k’ =  ((2m/ ħ²)[ U₀ – E])

ф-ция (x) внутри барьера экспоненциально уменьшается.

Внутри барьера  ф-ция отлична от нуля, это означает, что вероятность найти микрочастицу за барьером тоже отлична от 0. Микрочастица проникает в барьер

Классическая частица, обладая энергией E либо отразиться от барьера, либо пройдёт над ним, т.е. она не может проникнуть сквозь барьер.

R – коэф. отражения – отношение интенсивности отражённой волны, к падающей волне де Бройля

D – коэф. прозрачности – отношение числа микрочастиц прошедших через барьер (X >0) к числу частиц падающих на барьер.

R = |k₁ – k₂|²/|k₁ + k₂|²

D = 4k₁k₂/|k₁ + k₂|²

Чтобы барьер был конечным по ширине, сделаем третью область =>

(x) = A₁e^ik1x + B₁e^-ik1x

(x) = A₂e^ik2x + B₂e^-ik2x (B2 уже не будет равно нулю, т.к. отражённая волна может быть)

(x) = A₃e^ik3x + B₃e^-ik3x (B3 равен нулю, так как после барьера для микрообъекта нет препятствий и отразиться ему не от чего)

k₃ = ((2m/ ħ²)[E – U₀])

В обл. 3 U(x) = 0

k₃ = ((2m/ ħ²)E

Туннельный эффект – явление в рез-тате микрообъект может пройти через барьер.

Коэффициент прозрачности D потенциального барьера D = |A₃|²/|A₁|²

Для того, чтобы найти отношение |A₃|²/|A₁|², необходимо воспользоваться условиями непрерывности  и ’ на границах барьера x = 0 и x = l

₁(0) = ₂(0)

₁’(0) = ₂’(0)

₂ (l) = ₃(l)

₂’(l) = ₃’(l)

Эти четыре условия дают возможность выразить коэффициенты A2, A3, B1 и B2 через A1.

Совместное решение этих уравнений для прямоугольного потенциального барьера, в предположении, что коэффициент прозрачности мал по сравнению с единицей, даёт

D = D₀exp[(-2/ ħ) (2m(U - E))l]

U – Потенциальная высота

E – Энергия частицы

l – Ширина барьера

D₀ – постоянный множитель, который можно приравнять к единице

Для потенциального барьера произвольной формы имеем:

D = D₀exp[(-2/ ħ)^x1_x2(2m(U - E))dx], где U = U(x)

Туннельный эффект является специфическим квантовым эффектом

Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределённостей.

Неопределённость импульса ∆p> h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия (∆p)²/2m может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.

Основы теории туннельных переходов заложены работами Л.И. Мандельштама и М.А. Леонтовича.

19

Гармонический осциллятор.

Движение осуществляется под действием квазиупругой силы.

F= - cx, md²x/dt² + cx=0

x’’+cx/m = 0

ω₀² = c/m

Если частица двигается (возбужд сост), то вероятность обнаружить её в пределах от x до x+dx определяется временем dt нахождения частицы

dt₂<dt₁, W₂<W₁

W~1/υ – плотность вероятностей обнаружить частицу пр-ва обратно пропорционально υ0, W∞

Полная энергия частицы не изменяется, но в зависимости от величины x0 (от степени возбуждения) может иметь непрерывный ряд значений.

Квантовая частица (одномерный случай)

∂²Ψ/∂x² + 2m[E-U(x)] Ψ/ћ² = 0

Частица находится в потенциальном поле, на неё действует квазиупругая сила.

U(x)=cx²/2, c=mω₀²

U(x)= mω₀²x²/2

∂²Ψ/∂x² + 2m[E- (mω₀²x²/2)] Ψ/ћ² = 0

Решение этого уравнения позволяет определить собственные ф-ии Ψn(x) и собств значения энергии. Из решения следует, что квантовый гармонический осциллятор может принимать только дискретные значения эн-ии.

{{Для потенциал ящика:

E_n=n² ћ²(π/l)²/2m

Ψ_n(x)=√(2/l)*sin(nπx/l)}}

E_n=(1/2 + n)ћω₀, n=0,1,2… - квантовое число

Квантовый гармонич осциллятор не имеет нулевого значения энергии

Wкв=|Ψ|²

n=0

E_n=E₀= ћω₀²/2

Ψ₀(x)~ exp(-x²/2x²) / x^1/2

ω₀(x)= exp(-x²/x₀²) / x

Вероятность обнаружить квант частицу max но в отличие от классич, частицу можно обнаружить в любом другом месте и даже за пределами амплитуды x0

Вероятность обнаружить микрочастицу min при x=0 и max в 2-х координатах.

С увеличением квант числа число «горбов» увеличивается. Результирующая кривая может быть описана непрерывной ф-ией U(x).