Последние равенства и представляют собой основу для разработки различных методов решения матричных игр.

Таким образом, можно привести следующие условия приме-

остратегии второго игрока.

5.Допускается усреднение результатов игр.

Перейдем теперь к изучению методов решения матричных игр в смешанных стратегиях.

2.4. Решение матричной игры 2×2

Начнем рассмотрение методов нахождения оптимальных смешанных стратегий с простейшей игры, описываемой платежной матрицей

Пусть смешанные стратегии игроков имеют вид:

27

Откуда получаем следующее решение матричной игры:

Вычислив оптимальное значение n , можем вычислить и оптимальную смешанную стратегию второго игрока из условия a11q1 + a12 q2 = v , или a11q1 + a12 (1- q1 ) = v . А именно:

при a11 ¹ a12 .

Эту задачу можно решить и графически, учитывая, что решение системы (2.14) представляет собой геометрически точку пересечения двух прямых на плоскости ( p1 , n ) или (1 - p1 , n ).

Приведем алгоритм геометрического способа решения игры

2×2:

1. На оси абсцисс откладываем отрезок единичной длины p1 = p Î[0, 1].

решение матричной игры ( p10 , v).

28

Проиллюстрируем данный алгоритм на рисунке:

n

Решение. Определим сначала верхнюю и нижнюю цену игры:

Так как a < b , то имеем игру без седловой точки, что при-

водит к необходимости рассмотрения смешанной стратегии. По формулам (2.15) найдем:

n = 3 ×0,375 + 7 ×0,625 = 5,5 .

29

По формулам (2.15´) определим смешанную стратегию второго игрока:

Рис. 2.2

2.5. Матричные игры 2×n

Пусть платежная матрица игры имеет вид:

30

Тогда, согласно теореме 2.2, решение игры находится из уравнения:

построим ее график. Для этого надо построить n прямых вида:

выбрать ломанную, огибающую их снизу. Верхняя точка этой ломанной и дает решение игры.

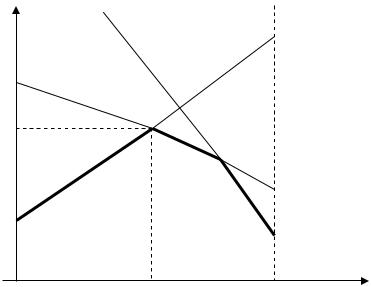
Геометрически это можно проиллюстрировать следующим образом:

w

n

Рис. 2.3

Здесь нижняя огибающая выделена жирной линией.

31

№ 2.6. Найти оптимальную стратегию первого игрока в матричной игре, заданной матрицей 2×3:

Решение. 1. Сначала проанализируем игру на наличие седловой точки:

Так как a < b , то седловой точки нет и надо искать решение

всмешанных стратегиях.

2.Вычислим средние выигрыши первого игрока, при условии, что второй игрок выбирает только чистые стратегии, при помощи таблицы:

решаем систему уравнений:

32

Найдем теперь оптимальную стратегию для второго игрока. Здесь в зависимости от формы нижней огибающей может представиться несколько случаев.

А. Нижняя огибающая имеет единственную точку максимума

( p0 ,n 0 ).

1. Если p0 = (0;1), то есть оптимальной стратегией первого игрока является стратегия A2 , то второму игроку выгодно применять чистую стратегию, соответствующую номеру прямой

33

( k 0 ), проходящей через точку( 0, n ) и имеющей наибольший отрицательный наклон.

w

n

(k0 )

Рис. 2.5

2. Если p0 = (1; 0) , то оптимальной для второго игрока яв-

ляется стратегия, соответствующая номеру ( k 0 ) соответствующей прямой, имеющей наименьший положительный наклон.

w

n

(k0 )

Рис. 2.6

34

3. Если 0 < pi0 <1 , то в оптимальной точке пересекаются, как минимум, две прямые:

w

n

Рис. 2.7

одна из которых ( k 0 ) имеет положительный наклон, а другая ( l 0 ) отрицательный. И оптимальная смешанная стратегия второго игрока получается при

где q0 является решением уравнения

a1k q + a1l (1 - q) a=2k q + a2l (1- q ) .

B. Нижняя огибающая имеет горизонтальный участок.

35

w

(k0 )

Рис. 2.8

Тогда оптимальной для второго игрока является чистая стратегия Bk0 .

Найдем теперь оптимальную стратегию второго игрока в нашей задаче.

1. Так как в оптимальной точке пересекаются первые две прямые, то

q1 = q, q2 = 1 - q, q3 = 0,

то есть из трех стратегий применяются первые две(активными являются B1 и B2 ).

2. Приравняем соответствующие средние выигрыши второго игрока с использованием таблицы:

36

а именно:

1× q + 3×(1- q ) + 0 ×5 = 4 × q + (1 - q )× 2 + 0 ×1 .

3. Решим последнее уравнение:

q + 3 - 3q 4q +=2 - 2q, 4q =1 ,

Следовательно, полное решение игры имеет вид:

2.6.Матричные игры m×2

Вэтом случае платежная матрица игры имеет вид:

Решение этой игры аналогично решению игры2 ´ n , только

в этом случае на плоскости(q,w) ищется минимум верхней огибающей прямых

37

wi = ai1q + ai 2 (1 - q), i =1, m .

Рассмотрим конкретный пример игры 3 ´ 2 .

№ 2.7. Найти решение игры 3 ´ 2 :

Решение. 1. Проанализируем игру на наличие седловой точки:

a1 =1, a2 = -2, a3 = 0, a = 1, b1 = 3, b2= 5, b= 3.

То есть a < b и необходимо применить смешанную страте-

гию.

2. Вычислим средние выигрыши второго игрока(при условии, что первый игрок выбирает только чистые стратегии). Из таблицы

получаем следующие прямые:

38

3. Построим верхнюю огибающую.

w

5

4

3

n

1

4

-2

Рис. 2.9

4. Так как наименьшее значение верхней огибающей получается как решение системы уравнений:

ìw =q + 4(1 - q ),

ï

í

ïîw = 3q - 2(1 - q ),

то получаем:

3q - 2(1 - q) =q + 4 (1 - q);

3q - 2 + 2q= q + 4 - 4q ;

39