
- •Номер Номер
- •Режим бегущих волн
- •Ток в линии
- •Волновое сопротивление
- •Режим стоячих волн
- •Разомкнутая линия
- •Уравнения линии без потерь в режиме холостого хода
- •Мгновенные значения напряжения и тока
- •Короткозамкнутая линия
- •Линия, нагруженная на реактивное сопротивление
- •Режим смешанных волн
- •Входное сопротивление линии, нагруженной на активное сопротивление,
Расчетно-графическое задание №4
Цепи с распределенными параметрами
Задание: Произвести расчет процессов в двухпроводной линии с распределенными параметрами по числовым параметрам, указанным в табл.2, в соответствии с выбранным вариантом.
Варианты задачи.
Двухпроводная линия без потерь с параметрами L0 и C0 находится в режиме холостого хода. Мгновенное значение напряжения (В) в конце линии определяется выражением
U2 = 400 sin (t + 30).
Для точки а , отстоящей от конца линии на расстоянии Ха = 12500 м, написать выражение для мгновенного значения тока, построить график зависимости этого тока от времени и вычислить входное сопротивление линии в этой же точке. Написать зависимость напряжения от координаты Х для двух моментов времени t1 и t2 и построить соответствующие графики. Определить расстояние от конца линии до ближайшей к нему точки, в которой действующее напряжение равно нулю.
Двухпроводная линия без потерь с параметрами L0 и C0 находится в режиме холостого хода. В точке а, удаленной от конца линии на расстояние Ха, напряжение (В) определяется выражением
Ua = 200 sin (t + 10).
Написать выражение для мгновенного значения тока в точке, удаленной от конца линии на расстояние Ха = 17500 м, и построить график зависимости этого тока от времени. Написать зависимости, показывающие распределение напряжения вдоль линии для двух моментов времени t1 и t2 и построить соответствующие графики.
Двухпроводная линия без потерь имеет параметры L0 и C0. В точке а, удаленной от конца линии на расстояние Ха, мгновенное значение тока (А) определяется выражением
i = 0,25 sin (t - 20).
Написать выражение для мгновенных значений напряжения в той же точке линии в двух случаях: а) линия на конце разомкнута; б) линия на конце замкнута накоротко.
В обоих случаях построить (на двух графиках) кривые распределения напряжения вдоль линии для моментов времени t1 и t2 (на первом графике две кривые, относящиеся к случаю а , на втором графике - две кривые, относящиеся к случаю б ).
Двухпроводная линия с параметрами L0 , R0 , C0 и G0 нагружена на характеристическое сопротивление. В точке а на линии, отстоящей от её начала на расстояние Ха, напряжение (В) определяется выражением
Ua = 100 sin (t + ).
Определить мгновенное значение тока в точке b, отстоящей от начала линии на расстоянии Хb. Для момента времени t1 построить кривые распределения тока и напряжения вдоль линии. Вычислить длину волны в линии.
Двухпроводная линия без потерь с параметрами L0 и C0 нагружена на сопротивление Z2. Определить значение Z2, если входное сопротивление нагруженной линии в точке а, отстоящей от конца линии на расстояние Х = 50000 м, равно нулю.
Определить мгновенное значение напряжения на нагрузке, если ток в точке а
i = 0,1 sin (t + 10) (А).
Построить кривые зависимости напряжения от координаты Х для моментов времени t1 и t2.
6. Двухпроводная линия длиной l1 имеет параметры L0 , R0 , C0 и G0. Определить, какую дополнительную индуктивность надо включить на каждую тысячу метров линии, чтобы передачу сигналов по линии можно было осуществлять без искажений. Полагая, что дополнительные индуктивности включены и линия нагружена на согласованное сопротивление, определить мгновенное значение напряжения U2 в конце линии, если напряжение в начале линии
U1 =[100 sin (t + 30) + 40 sin (t - 45)] (B).
Проанализировать полученное выражение для U2 и показать, что линия действительно не исказила передаваемый по ней сигнал.
Построить графики U1 = f1(t) и U2 = f2(t) за время, равное 2 миллисекундам.
Примечание. Чтобы убедиться в том, что передача сигнала по линии происходит без искажения, необходимо при написании выражения для U2 за начало отсчета времени взять не момент, когда t = 0, а момент когда t = t1 (t1 - это время, в течение которого падающая волна проходит расстояние, равное длине линии).
7. Длина двухпроводной линии без потерь меньше четверти длины волны. При нагрузке линии на активное сопротивление Z2 = R2 отношение модулей U2 / U1 = 1, а при холостом ходе линии отношение модулей U2 / U1= k. Здесь U2 иU1 - действующие значения напряжений соответственно в конце и начале линии. Определить входное сопротивление линии при коротком замыкании на конце, если скорость распространения электромагнитных волн 300000 км/с. Определить распределенные параметры линии L0 и C0.
Двухпроводная линия длиной l1 имеет параметры L0 , R0 , C0 и G0.
Линия питает нагрузку Z2 при частоте f. Определить затухание в линии в неперах и угол сдвига по фазе между напряжениями в начале и конце линии. Построить графики распределения мгновенного значения тока вдоль линии для моментов времени t1 и t2, полагая, что напряжение в конце линии
U2 = 141 sin (t - 23) (В).
9. Двухпроводная линия без искажения длиной l1 имеет параметры C0 и G0 и работает на согласованное сопротивление Z2 = R2. Напряжение в конце линии
U2 = [50 sin (t + 30) + 30 sin (t - 30)] (B).
Частоты заданы: f1 = 800 Гц и f2 = 1600Гц.
Написать выражение для мгновенного значения U1 в начале линии. Проанализировать полученное выражение и показать, что передача сигналов по линии происходит без искажения. Построить графики U1= F1(t) и U2 = F2(t) за время, равное двум периодам.
Примечание. Чтобы убедиться в том, что передача сигнала по линии происходит без искажения, необходимо при написании выражения для U1 за начало отсчета времени взять не момент, когда t = 0, а момент когда t = - t1 (t1 - это время, в течение которого падающая волна проходит расстояние, равное длине линии).
10. Две двухпроводные линии без потерь включены параллельно и работают на общую нагрузку Z2 = (500 + j 500). Мгновенные значения напряжений в начале обеих линий одинаковы. Длина первой линии l1, её волновое сопротивление Zc1= 600 Ом, а коэффициент фазы . Длина второй линии l2, её волновое сопротивление Zc2= 500 Ом, а коэффициент фазы . Напряжение на нагрузке (В) U2 = 110 sin (t + ).
Определить мгновенные значения токов в конце и в начале каждой линии.
11. Двухпроводная линия длиной l1 , питается от источника напряжения при частоте f , имеет параметры L0 , R0 , C0 и G0. Определить значение сопротивления нагрузки Z2, при которой в ней будет выделяться максимальная средняя мощность. Определить КПД линии в этом случае.
12. Двухпроводная линия без потерь длиной l1 питается от генератора на частоте f . Параметры линии L0 и C0 . Известно, что отношение действующего значения напряжения в точке а при коротком замыкании линии к действующему значению напряжения в этой же точке при холостом ходе линии равно k. Определить, как удалена эта точка от конца линии, если считать, что это расстояние меньше четверти длины волны. Построить зависимости напряжения и тока от времени в точке b, находящейся на расстоянии Хb от конца линии, если в начале линии напряжение (В)
U1 = 120 sin (t + 60),
а нагрузка линии Z2 = j 800 Ом.
13. Двухпроводная линия без потерь длиной l1 нагружена на активное сопротивление R2 = 600 Ом. Параметры линии L0 и C0. Написать выражение для мгновенного значения тока в начале линии, если напряжение генератора (В)
U1 = 141 sin (t + ).
Частота генератора f. Построить график зависимости тока от координаты Х для момента времени t1.
14. Двухпроводная линия без потерь длиной l1 имеет параметры L0 и C0. Напряжение питающего генератора (В)
U1 = 100 sin (t + )
при частоте f. На приемном конце линия разомкнута. Определить, в какой точке линии ток максимален и чему равно это максимальное значение. Построить кривые зависимости тока от координаты Х для двух моментов времени t1 и t2.
15. Двухпроводная линия нагружена на сопротивление Z2, вдвое большее волнового сопротивления линии. Напряжение питающего генератора (В)
U1 = U1m sin (t + ).
Написать выражение для мгновенного значения тока в начале линии, если известно, что входное сопротивление линии при коротком замыкании в конце равно Zвх к.з., а входное сопротивление линии при холостом ходе равно Zвх х.х. Построить график зависимости напряжения и тока от времени для точки а , равноудаленной от конца и от начала линии. Считать, что длина линии меньше половины длины волны.
16. Двухпроводная линия длиной 100 км нагружена на согласованное сопротивление. В начале линии известны комплексы напряжения U1 и тока I1 , а также напряжения U2 в конце линии.
Определить для этой линии параметры R0, G0, L0 и 1/C0. Найти входное сопротивление линии при коротком замыкании на конце.
17. Двухпроводная линия без потерь неоднородна и состоит из двух участков. Участок линии, прилегающий к источнику питания, имеет длину l1 и параметры Zc1 и а участок линии, прилегающий к нагрузке, имеет длину l2 и параметры Zc2 и .
Написать выражение для напряжения как функции времени и положения точки на линии в случае, когда в начале поддерживается напряжение (В)
U1 = 100 sin (t - 60),
а на конце линия разомкнута. Ответ должен содержать два выражения: одно справедливо для первого участка линии, второе - для второго. Построить графики распределения напряжения вдоль линии для двух моментов времени t1 = 0,175 mC и t2 = 0,262 mC.
18.Двухпроводная линия длиной l1 имеет параметры R0, G0, L0 и C0. Линия работает в режиме короткого замыкания. Действующее значение тока на конце линии I2. Определить мощность, отдаваемую в линию питающим генератором, при частоте f.
Таблица 2



Номер Номер
вари- задачи
ант а Исходные данные




















Краткие теоретические сведения
В современной радиотехнике всё более широкое применение находят устройства, геометрические размеры которых соизмеримы или больше длины волны распространяющихся в них электромагнитных колебаний. Например, рассматривая передачу электромагнитной энергии в линиях связи, фидере, волноводе, антенне и т.п., следует учитывать, что магнитные и электрические поля распределены по всей длине этих устройств, и превращение электромагнитной энергии в тепло также происходит по всей длине устройств. Такие цепи характеризуются распределёнными по всей длине индуктивностями, ёмкостями, активными сопротивлениями и называются цепями с распределёнными параметрами.
Воздействие генератора на такую цепь проявляется в некоторой точке цепи не мгновенно, а с запаздыванием на время, определяемое длиной пути тока между генератором и этой точкой и скоростью распространения колебаний в цепи. Поэтому мгновенное значение тока в реальной цепи с конечными размерами принципиально не может быть везде одинаково.
Простейшими цепями
с распределёнными параметрами являются
длинные линии
(двухпроводные воздушные линии связи,
симметричные и коаксиальные кабельные
линии проводных систем связи, полосковые
линии передачи и т.п., имеющие длину
![]() ,
- длина волны
электромагнитных колебаний).
,
- длина волны
электромагнитных колебаний).
Уравнения однородной линии передачи
Линии передачи, геометрическая конфигурация, а также свойства материалов (проводников и диэлектриков), которых остаются неизменными по всей длине, называются однородными, или регулярными.
Рассмотрим в качестве примера двухпроводную линию передачи с известным сопротивлением нагрузки на конце (рис. 54).
Электромагнитные свойства такой линии характеризуются первичными параметрами, т. е. параметрами, отнесёнными к единице длины линии:
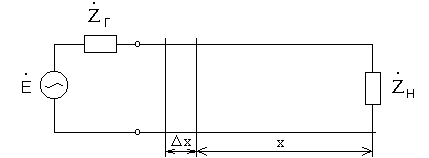
Рис. 54
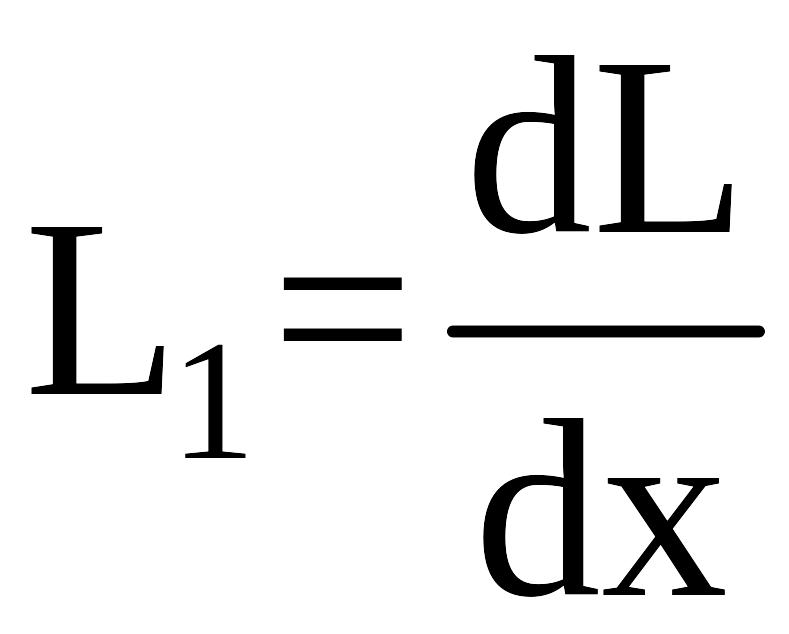 погонная
индуктивность, Гн / м;
погонная
индуктивность, Гн / м;
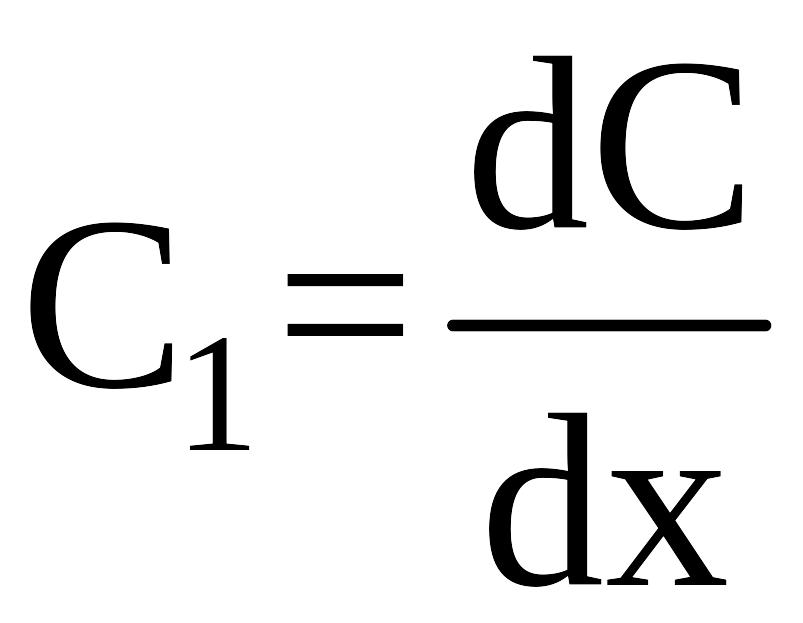 погонная
емкость, Ф / м;
погонная
емкость, Ф / м;
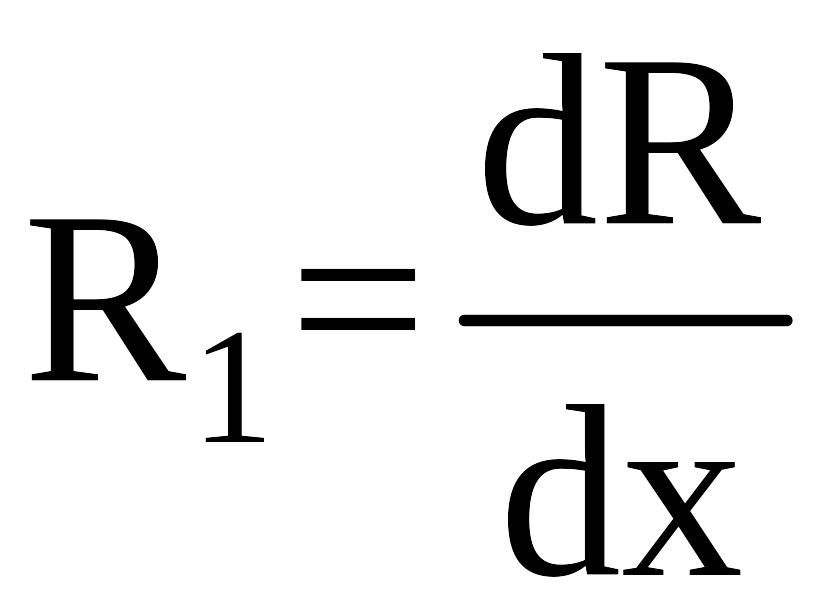 погонное
сопротивление, Ом / м;
погонное
сопротивление, Ом / м;
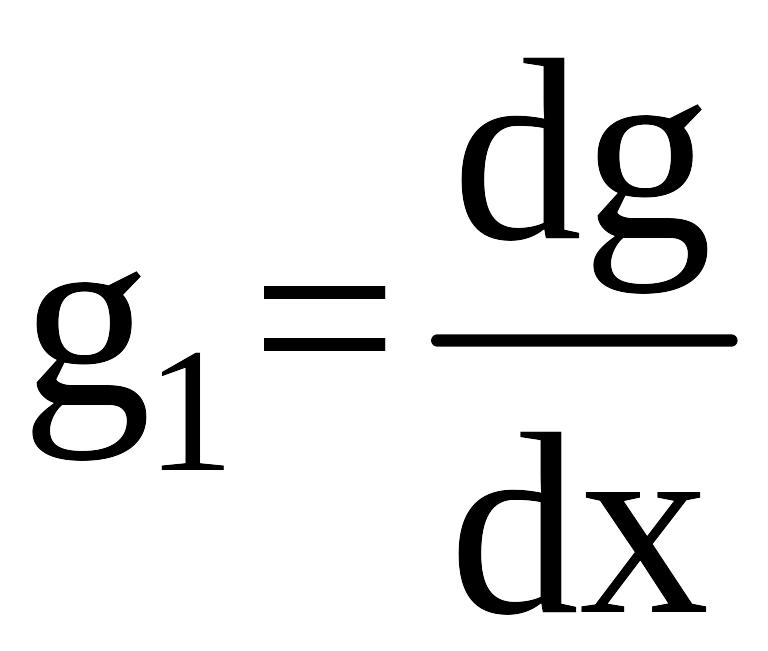 погонная
проводимость, Сим / м.
погонная
проводимость, Сим / м.
Строгое решение задачи о зависимости тока в линии от времени и координаты х может быть получено из системы уравнений Максвелла. Однако этот метод имеет существенный недостаток, заключающийся в том, что решение системы уравнений Максвелла удаётся довести до конца только для ограниченного класса линий передачи с достаточно простой конфигурацией.
Если же представить длинную линию в виде отрезков длиной X каждый, то в пределе при X0 такие малые элементы линии могут быть описаны методами, принятыми в теории цепей. В этом случае любой малый отрезок линии можно представить в виде эквивалентной схемы (рис. 55), состоящей из сосредоточенных малых элементов L=L1X, C=C1X, R= R1X, g= g1X.

Рис. 55 Рис. 56
Вся же линия может
быть представлена каскадным соединением
элементарных четырёхполюсников (рис.
56), где Z1= R1+jL1
погонное
комплексное сопротивление,
Y1= g1+jC1
погонная
комплексная
проводимость.
Обозначив символами
![]() комплексные амплитуды напряжений и
токов соответственно на входе и выходе
элементарного четырёхполюсника для
внутреннего контура и узла А
на основании
второго и первого законов Кирхгофа,
получим тождества
комплексные амплитуды напряжений и
токов соответственно на входе и выходе
элементарного четырёхполюсника для
внутреннего контура и узла А
на основании
второго и первого законов Кирхгофа,
получим тождества
![]() ,
,
![]() .
.
С точностью до малых величин второго порядка
![]() .
.
Представим последние тождества системой разностных уравнений:

Совершая
предельный переход при
![]() ,
получим систему двух дифференциальных
уравнений с постоянными коэффициентами,
которые называются телеграфными
уравнениями
,
получим систему двух дифференциальных
уравнений с постоянными коэффициентами,
которые называются телеграфными
уравнениями
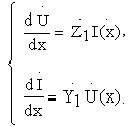
Если продифференцировать обе части телеграфных уравнений по х, то последняя система может быть сведена к двум дифференциальным уравнениям второго порядка как относительно напряжения, так и относительно тока:
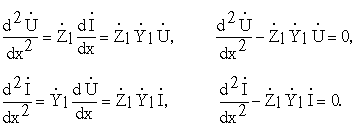
В теории волновых процессов эти уравнения носят название уравнений Гельмгольца, их общее решение записывается следующим образом:
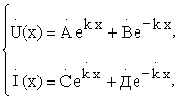
где
![]()
комплексный
коэффициент распространения.
комплексный
коэффициент распространения.
Первые слагаемые в выражениях для напряжения и тока определяют комплексные амплитуды падающих волн, а вторые отраженных волн напряжения и тока.
Постоянные интегрирования определяются из начальных условий:
![]()
и
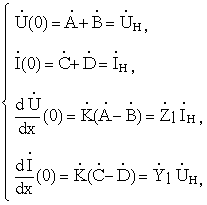
отсюда
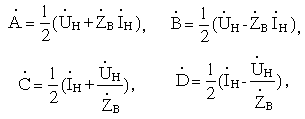
где

волновое сопротивление линии.
волновое сопротивление линии.
Подставив постоянные
интегрирования в уравнения для
![]() и
и
![]() ,
получим
,
получим
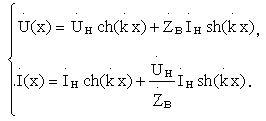
Для линии без потерь R1 = g1 = 0,
![]() ,
,
где фазовая постоянная, показывающая отставание фазы колебаний за время их распространения на единице длины.
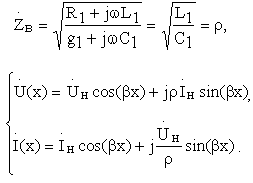
В зависимости от соотношения сопротивления нагрузки и волнового сопротивления линия работает в режиме бегущих, стоячих или смешанных волн.
