2 Обобщённая статистическая модель технологического процесса

2.1 Управляемость процесса.

Любой процесс изготовления продукции характеризуется технологической возможностью производства. Под технологической возможностью производства понимается не только и не столько привычная и понятная всем количественная сторона – производительность, но и его качественная сторона, представленная чаще всего в виде среднего значения группового показателя качества и его дисперсии. Причём среднее и дисперсия вполне характеризуют как измеримые признаки качества, так и неизмеримые – качественные (альтернативные).

В самом деле, если групповым показателем качества является уровень несоответствий конечной совокупности (партии) изделий, выраженный в виде абсолютного значения несоответствующих изделий в ней или доли несоответствующих изделий в партии (или числа несоответствий на 100 единиц продукции), то для любого показателя качества его групповой аналог всегда можно представить в виде распределения, соответствующего (по крайней мере асимптотически, при n  ) нормальному закону. Чтобы показать это, предположим, что в результате опробования технологического процесса (или отдельной операции) получено m пробных партий. Тогда в результате выборочного контроля этих партий можно получить оценку среднего значения несоответствующих изделий в каждой партии (см., например, / /):

, (2.1)

где d_i – число несоответствий в i-ой партии;

N_i и n_i соответственно объем пробной партии и объем выборки из нее, используемые для оценки .

Несмещенная оценка дисперсии будет равна / /:

(2.2)

Согласно Центральной предельной теореме асимптотически нормальное при N   и (или) m   (где N =  ) приближение для обобщенного группового показателя качества можно получить, приняв в качестве параметров распределения этого показателя значения:

(или в виде доли: q_cp = /N, где N = ); (2.3)

, (или, соответственно, D[q]= ), (2.4)

рассчитанные по результатам выборочного контроля m пробных партий.

Естественно, аналогичные оценки можно получать не только по пробным партиям, но и по партиям изделий, предназначенным для потребителей. Кроме того, получая эти оценки в разные периоды времени, можно исследовать динамику их изменения.

Пусть у – обобщенный показатель качества продукции (размер, масса, электрическая емкость, глубина пропитки, количество сколов и т.п.). Каждое значение у_i для i‑го изделия является следствием возмущений от l операций, из которых состоит технологический процесс изготовления, и t внешних воздействий (температура, влажность, вибрации и т.п.). Среднее значение  и дисперсия ² группового показателя качества N изделий, т.е. партии, также являются следствием l технологических операций и t воздействующих факторов. Из теории вероятностей и статистики известно, что дисперсия является строго аддитивной величиной:

(2.5)

(иногда сумму (2.5) удобней записывать в виде:

, (2.6)

подразумевая, что каждое внешнее воздействие по-своему влияет на разных операциях).

Технологический процесс является абсолютно управляемым, если выполняются три условия:

1. процесс исследован, т.е. все возмущения выявлены (идентифицированы) и минимизированы по крайней мере до такой степени, что отсутствуют один, два или максимум три операции и (или) внешних воздействующих фактора, вносящих преобладающий вклад в сумму (2.5) или (2.6). С математической точки зрения это означает выполнение условий Центральной предельной теоремы, причем на "физическом" уровне, т.е. вклад в общую дисперсию процесса каждой технологической операции и каждого внешнего воздействующего фактора оценён и проверен экспериментально;

2. технологический процесс является регулируемым, т.е. организован так, что имеется главная обратная связь в виде рычага, вентиля, электрического импульса и т.п., с помощью которого можно весь процесс подстроить, не останавливая его (если процесс состоит из отдельных операций, имеющих самостоятельное значение, то, естественно, каждая такая операция должна быть управляема в указанном выше смысле или должна включать на выходе сплошной контроль с отсортировкой несоответствующих изделий - заготовок, по крайней мере, – выборочный контроль с более жёстким планом, чем план контроля на выходе всего процесса);

3. процесс как объект регулирования устойчив, т.е. размах признаков качества R = y_max– y_min на выходе процесса для любой совокупности конечного объема не превышает значения z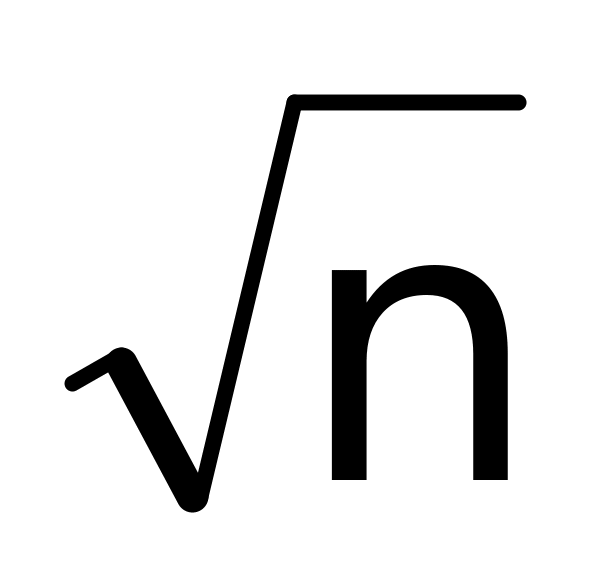_/ при одностороннем ограничении признака качества или 2z_1+/2/ для случая двустороннего ограничения признака качества (где y_max и y_min – соответственно, максимальное и минимальное значение обобщённого признака качества; z_ – квантиль стандартной нормальной функции распределения уровня ;   0,9 – уровень доверия, чаще всего принимаемый равным 0,95; n – объём выборки).

Если процесс является абсолютно управляемым, т.е. выполняются все три условия, то в этом случае вводить приемочный контроль в виде обязательной операции, в частности выборочный контроль, нецелесообразно. Контроль в этом случае можно осуществлять только периодически (контроль с пропуском партий, контроль по требованию заказчика или органа сертификации и т.п.). Выборочный контроль каждой партии целесообразен, если не выполняется любое из двух последних условий или оба вместе. При невыполнении всех трех условий необходим сплошной контроль. Если же не выполняется первое условие, то выборочный контроль по соответствующим стандартам возможен только по альтернативному признаку, поскольку все стандартные системы выборочного контроля разработаны исключительно для нормально распределенных количественных признаков качества.