6.4 Связь фактического уровня несоответствий в партии с его верхней и нижней доверительными границами при стабильной (известной) дисперсии и одностороннем ограничении признака качества

Часто появляется необходимость в получении точечной оценки уровня несоответствий в партии q_т, располагая по результатам приёмочного контроля только значением верхней доверительной оценки q_в. При одностороннем ограничении нормально распределенного показателя качества со стабильной (известной) дисперсией точечная (в литературе она иногда называется «фактической») оценка уровня несоответствий определяется по формуле:

(6.23)

где - среднее значение признака качества контролируемой партии, оцениваемое по результатам выборочного контроля.

Верхняя граница уровня несоответствий партии определяются по формулам (см. п. 6.1):

(6.24)

где - верхняя доверительная граница среднего значения признака качества партии, оцениваемая по выборке с уровнем доверия  для планов поставщика и  для планов потребителя;

- аналогичная нижняя доверительная граница;

- квантиль стандартного нормального распределения уровня  для плана поставщика и уровня  для плана потребителя;

n – объем выборки;

 - стабильное и поэтому известное значение стандартного отклонения признака качества партии, согласованное между поставщиком и потребителем.

Чтобы найти связь между уровнем q_т и верхней границей уровня несоответствий q_в подставим в (6.24) выражения для _в и _н:

(6.25)

Из (6.23), переходя к квантилям, можно получить:

(6.26)

С учетом соотношения (6.26) выражение (6.25) можно представить в следующем виде:

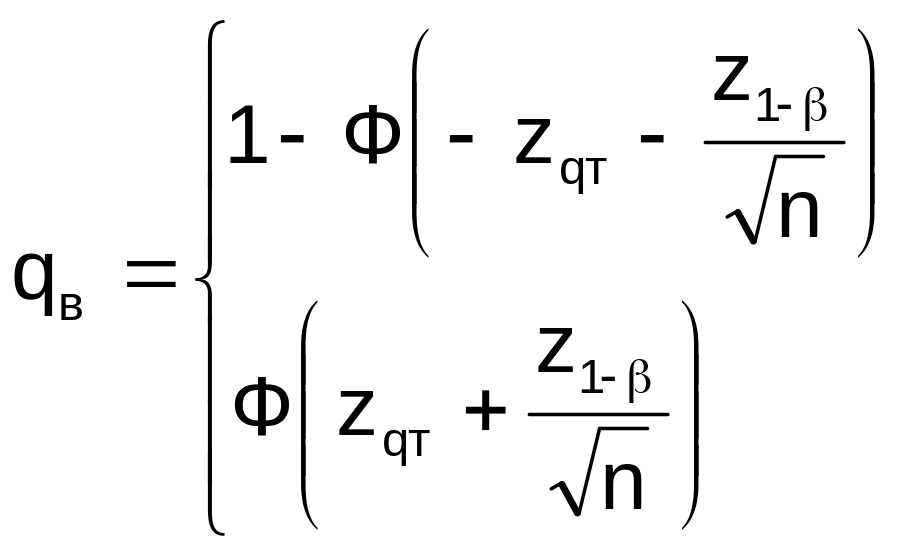
или окончательно:

(6.27)

при любом одностороннем ограничении признака качества.

Аналогично можно получить связь между квантилями фактического уровня несоответствий и нижней границы уровня несоответствий партии для планов потребителя:

(6.28)

(Интересно отметить, что в случае   0,5, т.е. для степеней доверия Т6 и Т7 по группе ГОСТ Р 50779 расчетная верхняя граница уровня несоответствий  q_в будет иметь значение меньше значения точечной оценки уровня несоответствий q_т, поскольку в этом случае 1‑ < 0,5 и, следовательно, z_1-< 0. При  = 0,5, т.е. при степени доверия Т4, q_т = q_в. Для планов потребителя нижняя граница уровня несоответствий партии всегда будет меньше фактического уровня, поскольку в стандартах установлено ограничение   0,1, а для таких значений риска поставщика при контроле потребителя всегда z_1‑ > 0. При степени доверия Т7 ( = 0,9) и установленном максимальном значении  = _max = 0,1 квантили z_1- и z_1- окажутся равными, но с противоположными знаками и поэтому в этом случае верхняя граница уровня несоответствий для плана поставщика будет равна нижней границе для плана потребителя, т.е. q_в = q_н).

Соотношения (6.27) и (6.28) позволяют сравнительно просто пересчитывать фактические уровни несоответствий в граничные значения (с заданным уровнем доверия) и обратно. Например, при построении характеристик планов выборочного контроля уровни несоответствий партии, откладываемые по оси абсцисс, можно выражать либо в q_т, либо в граничных значениях q_в для планов поставщика или в q_н для планов потребителя. Эти соотношения удобно использовать для последующего анализа планов выборочного контроля.

6.5 Связь точечной («фактической») оценки уровня несоответствий в партии продукции q_т с его интервальными оценками q_в и q_н при стабильной (известной) дисперсии  и двустороннем ограничении признака качества (изделие годное, если a  y_i  b).

В общем виде формулу (6.5) для вычисления верхней доверительной границы уровня несоответствий в партии q_в можно записать следующим образом:

(6.29)

где

Аргументы функций стандартного нормального распределения в (6.29) удобно представить в виде:

(6.30)

где - отношение половины поля допуска показателя качества к стандартному отклонению;

y* = (а + в)/2 – середина поля допуска;

(6.31)

Из (6.31) следует:

(6.32)

Точечная оценка уровня несоответствий в партии определяется соотношением:

(6.33)

где С_qт= при попаданий в любую половину поля допуска признака качества.

Сравнивая (6.33) с (6.32) с учетом (6.31) легко установить, что:

(6.34)

Для планов контроля потребителя соотношения для С_qт можно записать в виде:

(6.35)

где  - риск поставщика при входном контроле у потребителя.

Таким образом, в общем виде соотношения для q_в, q_н и q_т можно представить в виде:

(6.36)

Если рассматривать соотношения (6.36) как уравнение относительно С_q* при заданном  значении q* = q_т, q* = q_в  NQL для планов контроля поставщика или q* = q_н  NQL для планов контроля потребителя, то можно установить, что в обоих случаях каждому конкретному значению NQL по уравнению (6.36) удовлетворяют два симметричных корня:

С_{q 1, 2} = , (6.37)

соответствующих случаям попадания выборочного среднего в левую или правую половину поля допуска (ниже везде под C_q будем понимать положительное значение корня уравнения (6.36)). Решения уравнения (6.36) для разных значений q* и / представлены в таблице 6.2. По таблице 6.2 можно определить максимально допустимые значения , соответствующие заданным значениям NQL и /, такие, что при выполнении по результатам выборочного контроля условия:

(6.37)

партию нельзя отправлять потребителю, поскольку в этом случае для нее не выполняется условие:

q_в  NQL.

В отличие от случая одностороннего ограничения признака качества, при двустороннем ограничении связь точечной оценки q_т с доверительной верхней q_в или нижней q_н интервальной оценкой уровня несоответствий партии более сложная. Для пересчета q_т в q_в или q_т в q_н или наоборот необходимо использовать соотношения (6.34) и (6.35) с последующим расчетом q_н; q_в или q_т по (6.32) или (6.33). При этом очевидно, что при двустороннем ограничении признака качества и заданном значении всегда выполняется условие:

Таблица 6.2 Значения C_q в зависимости от значений NQL и 

	Значения Cq при NQL, равном:
	0,15%	0,25%	0,40%	0,65%	1,00%	1,50%	2,50%	4,00%	6,50%	10,00%	15,00%	25,00%
2,6	-	-	-	-	-	-	-	-	-	-	-	0,5104
2,8	-	-	-	-	-	-	-	-	-	-	-	0,6625
3	-	-	-	-	-	-	-	-	-	-	-	0,7905
3,2	-	-	-	-	-	-	-	-	-	-	0,4793	0,9062
3,4	-	-	-	-	-	-	-	-	-	-	0,6188	1,0150
3,6	-	-	-	-	-	-	-	-	-	0,4443	0,7395	1,1200
3,8	-	-	-	-	-	-	-	-	-	0,5801	0,8507	1,2227
4	-	-	-	-	-	-	-	-	0,4220	0,6983	0,9569	1,3241
4,2	-	-	-	-	-	-	-	-	0,5537	0,8080	1,0602	1,4248
4,4	-	-	-	-	-	-	-	0,3908	0,6695	0,9132	1,1619	1,5252
4,6	-	-	-	-	-	-	-	0,5208	0,7776	1,0158	1,2628	1,6254
4,8	-	-	-	-	-	-	0,3933	0,6352	0,8818	1,1172	1,3632	1,7255
5	-	-	-	-	-	-	0,5178	0,7424	0,9839	1,2179	1,4634	1,8255
5,2	-	-	-	-	-	0,3917	0,6293	0,8460	1,0850	1,3182	1,5635	1,9255
5,4	-	-	-	-	-	0,5122	0,7349	0,9478	1,1855	1,4183	1,6635	2,0255
5,6	-	-	-	-	0,4516	0,6216	0,8377	1,0486	1,2857	1,5184	1,7636	2,1255
5,8	-	-	-	0,3876	0,5635	0,7261	0,9390	1,1490	1,3858	1,6184	1,8636	2,2255
6	-	-	-	0,5034	0,6691	0,8282	1,0396	1,2492	1,4859	1,7184	1,9636	2,3255
6,2	-	-	0,4299	0,6105	0,7716	0,9292	1,1398	1,3493	1,5859	1,8184	2,0636	2,4255
6,4	-	0,3691	0,5401	0,7137	0,8728	1,0296	1,2400	1,4493	1,6859	1,9184	2,1636	2,5255
6,6	0,2976	0,4828	0,6445	0,8152	0,9733	1,1298	1,3401	1,5493	1,7859	2,0184	2,2636	2,6255
6,8	0,4183	0,5887	0,7465	0,9158	1,0735	1,2299	1,4400	1,6493	1,8859	2,1184	2,3636	2,7255
7	0,5264	0,6912	0,8474	1,0161	1,1737	1,3299	1,5400	1,7493	1,9859	2,2184	2,4636	2,8255
7,2	0,6298	0,7922	0,9477	1,1163	1,2736	1,4299	1,6400	1,8493	2,0859	2,3184	2,5636	2,9255
7,4	0,7313	0,8928	1,0479	1,2162	1,3736	1,5299	1,7400	1,9493	2,1859	2,4184	2,6636	3,0255
7,6	0,8319	0,9930	1,1479	1,3162	1,4735	1,6300	1,8400	2,0494	2,2859	2,5184	2,7636	3,1255
7,8	0,9321	1,0930	1,2479	1,4162	1,5736	1,7300	1,9400	2,1493	2,3859	2,6184	2,8636	3,2255
8	1,0324	1,1930	1,3479	1,5162	1,6736	1,8300	2,0400	2,2493	2,4859	2,7184	2,9636	3,3255
8,4	1,2323	1,3929	1,5479	1,7162	1,8737	2,0299	2,2400	2,4493	2,6859	2,9184	3,1636	3,5255
8,8	1,4323	1,5929	1,7479	1,9162	2,0737	2,2299	2,4400	2,6493	2,8859	3,1184	3,3636	3,7255
9,2	1,6323	1,7929	1,9479	2,1162	2,2737	2,4299	2,6400	2,8493	3,0859	3,3184	3,5636	3,9255
9,6	1,8323	1,9929	2,1479	2,3162	2,4737	2,6299	2,8400	3,0493	3,2859	3,5184	3,7636	4,1255
10	2,0323	2,1929	2,3479	2,5162	2,6737	2,8299	3,0400	3,2493	3,4859	3,7184	3,9636	4,3255

q_н  q_т  q_в,

т.к. и  0 при любом значении  и  из диапазона от 0 до 1.