5.3.3 Планы выборочного контроля при неизвестной дисперсии и одностороннем ограничении признака качества

Если дисперсия ² заранее неизвестна, то соотношения для уровня несоответствий в партии (5.1) – (5.3) содержат две неизвестные величины и, следовательно, помимо математического ожидания по выборке следует оценить и стандартное отклонение . В качестве эффективной, несмещённой и асимптотически нормальной оценки для стандартного отклонения используют её выборочное значение:

.

Однако, как и в случае с математическим ожиданием непосредственно использовать эту оценку в формулах нельзя. Действительно, известно, что отношение подчиняется распределению ² с n-1 степенью свободы. Тогда, например, в случае ограничения показателя качества снизу (изделие годное, если у_i  а), аналог аргумента в соотношении (5.2) для уровня несоответствий в партии можно записать в следующем виде:

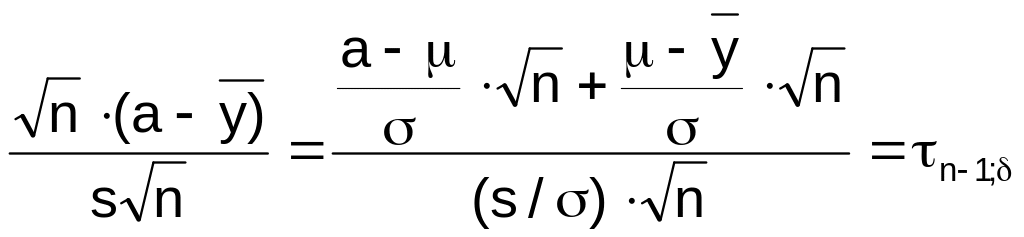, (5.14)

где величина _n-1; - имеет нецентральное распределение Стьюдента с n-1 степенью свободы и параметром нецентральности:

 =  .

Для получения параметров планов контроля можно непосредственно использовать статистику (5.14), но можно получить и более простое приближение в виде, аналогичном (5.9):

≥ а + k×s.

Т.е. партия соответствует требованиям, если случайная величина  =  - k×s превышает нижнее предельное значение для признака качества а, т.е. если   а. Тогда, используя асимптотическую нормальность выборочного стандартного отклонения s  no(; ), случайную величину  можно считать распределённой по нормальному закону с параметрами:

М[] =  - k× и D[] =  = .

Поэтому ОХ для случая одностороннего нижнего ограничения при неизвестной дисперсии можно представить в виде;

L() = P(  а) = 1 -  Ф или

L(q) = Ф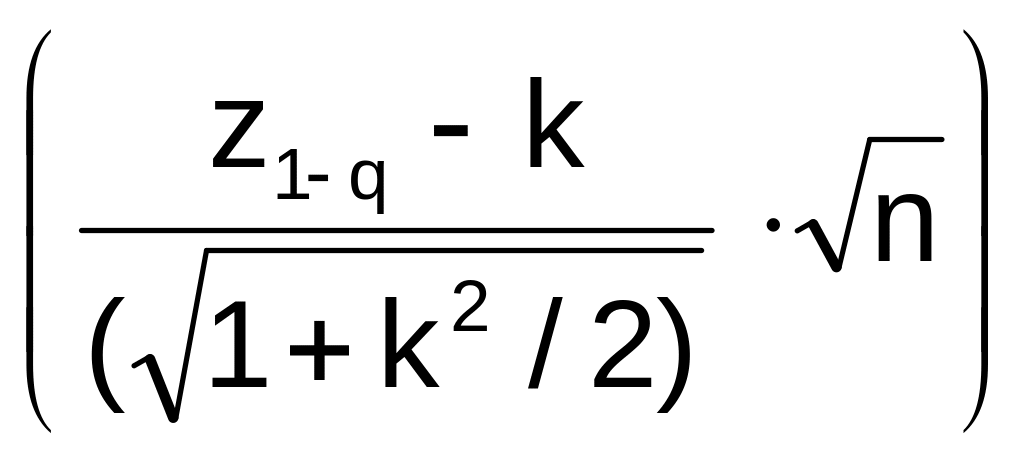 . (5.15)

Примечание. В литературе / / предлагается более точная формула:

L(q) = Ф .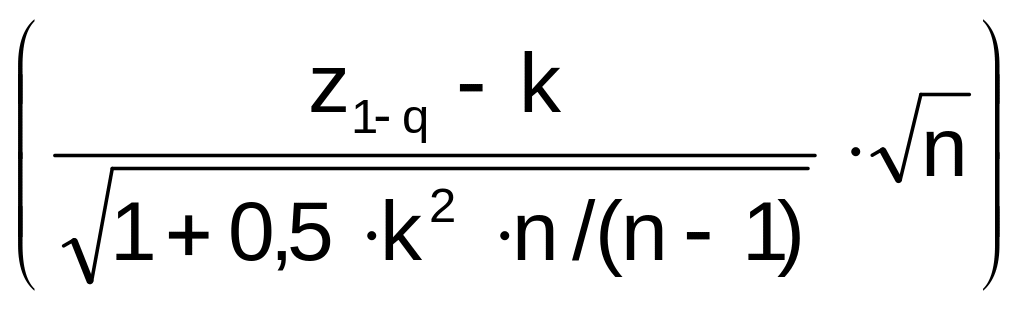

Если теперь как и в случае известной дисперсии считать, что ОХ, вычисляемая по формуле (5.15), должна проходить через точки с координатами (q = AQL; 1-) и (q = RQL; ), то нетрудно получить выражения для приёмочного коэффициента и объёма выборки (Получите!):

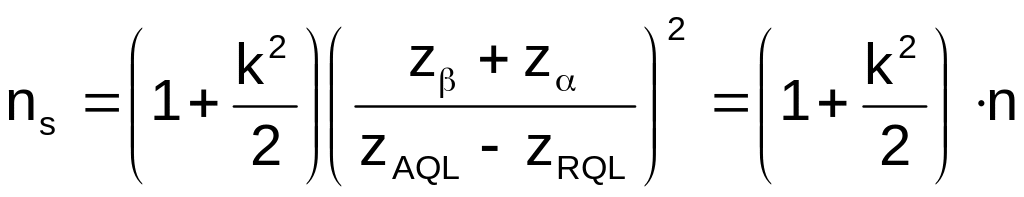; (5.16)

. (5.17)

Естественно, точно такие же соотношения получаются и в случае неизвестной дисперсии и одностороннем верхнем ограничении признака качества (изделие годное, если показатель качества у  b). Таким образом, при неизвестной дисперсии и любом одностороннем ограничении признака качества приёмочные коэффициенты такие же, как и при известной дисперсии, а объём выборки при прочих равных условиях в случае неизвестной дисперсии будет в раз больше, чем в случае, когда дисперсия известна.

5.3.4 Планы выборочного контроля при двухстороннем ограничении признака качества

В случае, если показатель качества у ограничен с двух сторон, т.е. изделие годное при а ≤ у_i  ≤ b, построение планов выборочного контроля несколько усложняется. В этом случае доля несоответствующих изделий состоит из двух частей: из доли изделий со значениями признака качества больше верхней границы допуска и доли изделий со значениями признака меньше нижней границы допуска:

Если построить график зависимости q(), он будет выглядеть в виде «перевёрнутого колокола» (см. рисунок 5.7) с минимумом в середине допуска  = у* = (а+ b)/2:

, (5.18)

г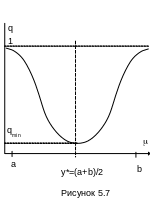 де обозначено  = b – а – поле допуска.

Следовательно, если в договоре между поставщиком и потребителем установлено нормативное значение группового показателя качества q_o в виде предельно допустимого уровня несоответствий менее q_min по (5.18), то контроль такого значения выборочными методами невозможен, т.к. заведомо будут получаться результаты с уровнем несоответствий в партии q_п > q_o. Соотношение (5.18) обычно используют для определения максимального значения дисперсии, точнее отношения  к полю допуска , при котором выборочные методы допустимы. Действительно, если должно соблюдаться условие:

,

то, переходя к квантилям, и после несложных преобразований получим:

  2 z_1-qo/2 . (5.19)

В системе AQL партия считается несоответствующей требованиям, если соотношение (5.19) не выполняется (см. табл. IV ГОСТ Р 50779.74).

Вторая особенность планов контроля с двусторонним ограничением показателя качества в том, что ОХ плана контроля в этом случае представляет собой симметричную кривую, монотонно возрастающую по мере удаления математического ожидания от середины поля допуска. Оперативная характеристика плана выборочного контроля равна вероятности попадания выборочного среднего в пределы [НПГ, ВПГ], где НПГ и ВПГ соответственно нижний и верхний пределы для выборочного среднего у партии, соответствующей требованиям к её качеству:

, (5.20)

где: d = y* - 

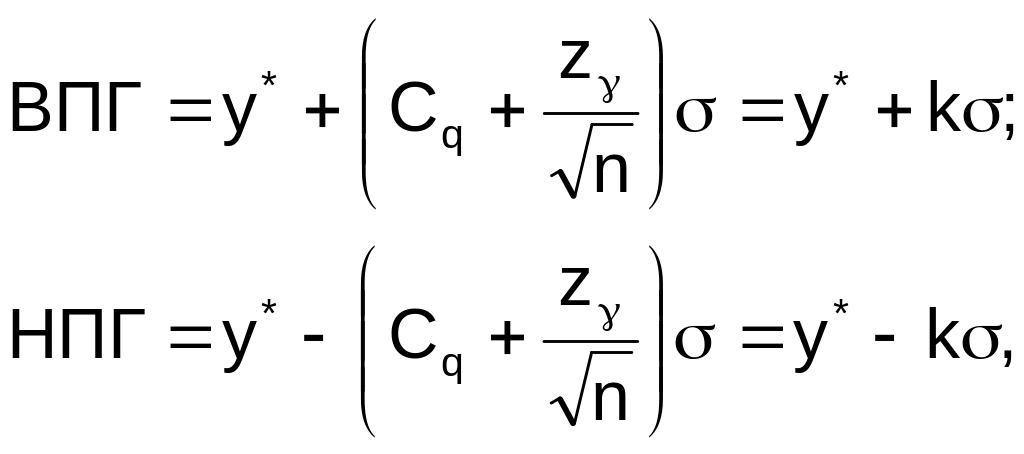
где C_q для установленных значений q_o и / определяется из уравнения:

;

- аналог приемочного коэффициента для случая двустороннего ограничения признака качества, который показывает, на сколько выборочное среднее может отклоняться от середины допуска y*, чтобы выполнялось условие приемки партии.

Естественно, в этом случае получить простые как в случае одностороннего ограничения формулы для приёмочного коэффициента и объёма выборки не представляется возможным.