Константа растворимости (произведение растворимости)
Если из пересыщенного раствора малорастворимого сильного электролита AхBy некоторая часть его выпала в осадок в виде кристаллов, то раствор над осадком при данных условиях является насыщенным относительно этого вещества. Между веществом в растворе (р) и кристаллическим осадком (к) устанавливается динамическое равновесие:
AхBy (к) ↔ хAy+(р) + yBx–(р).
Поскольку концентрация твердой фазы (осадка) с(KхAy) является величиной постоянной, математическое выражение константы данного равновесия имеет вид:
K = сx(Ay+) · сy(Bx–).
Такая константа [равновесия] называется константой растворимости (Ks) или произведением растворимости (ПР) малорастворимого электролита:
Ks (AхBy) = ПР (AхBy) = сx(Ay+) · сy(Bx–).
Таким образом, в насыщенном растворе малорастворимого сильного электролита произведение концентраций его ионов в степенях, равных стехиометрическим коэффициентам в уравнении диссоциации, при данной температуре есть величина постоянная, называемая константой растворимости или произведением растворимости. Ее значения приводятся в справочных таблицах (приложение 3).
Произведение растворимости характеризует сравнительную растворимость однотипных малорастворимых сильных электролитов: чем больше ПР данного вещества, тем больше его растворимость.
Условие образования осадка: Осадок AхBy образуется, если произведение концентраций (ПК) ионов Ay+ и Bx–, каждая из которых возведена в степень соответствующего стехиометрического коэффициента, больше величины ПР (AхBy):
ПK = сx(Ay+) · сy(Bx –) > ПР (AхBy).
Раствор, в котором создается это условие, – пересыщенный относительно данного электролита, из такого раствора будет выпадать осадок.
Данное условие может достигаться, например, при смешивании растворов, содержащих достаточные количества ионов Ay+ и Bx– или введении их дополнительных количеств в насыщенный раствор AхBy.
Условие растворения осадка: Осадок AхBy растворяется в воде, если в растворе над ним произведение концентраций (ПК) ионов Ay+ и Bx–, каждая из которых возведена в степень соответствующего стехиометрического коэффициента, меньше величины ПР (AхBy):
ПK = сx(Ay+) · сy(Bx –) < ПР (AхBy).
В данном случае раствор над осадком AхBy является ненасыщенным относительно этого вещества и его кристаллы будут растворяться в таком растворе.
Условия сx(Ay+) · сy(Bx –) < ПР (AхBy) можно достигнуть, например, при смешивании растворов, содержащих недостаточные количества ионов Ay+ и Bx– или введении в раствор над осадком растворителя (воды). Можно также вводить в раствор над осадком вещества, которые связывают ионы Ay+ и Bx–, образующиеся при переходе осадка в раствор.
По величине ПР может быть найден коэффициент растворимости (растворимость) s (моль/дм3) данного вещества. Для бинарных электролитов АВ их ПР и растворимость s связаны соотношением
ПР(АВ) = s2(АВ).
Например, между осадком BaSO4 и его насыщенным раствором устанавливается динамическое равновесие:
BaSO4 (к) ↔ Ba2+(р-р) + (р-р).
Из этого уравнения видно, что с(Ba2+) = c( ) = s(BaSO4).
Поскольку ПР(BaSO4) = с(Ba2+) · c( ), то справедливо выражение: ПР(BaSO4) = s2 (BaSO4). Отсюда следует:
s(BaSO4)
=
Пример 1.6.5. Произведение растворимости Ag2SO4 равно 1,6 ∙ 10–5 (25 оС). Определите растворимость этой соли в моль/дм3 и в г/дм3.
Решение.
1. Напишем схему равновесия между осадком и раствором и выражение для ПР данной соли:
Ag2SO4 (к) ↔ 2Ag+(р-р) + (р-р);
ПР(Ag2SO4) = с2(Ag+) ∙ с( ).
2. Выразим концентрации ионов Ag+ и в растворе над осадком через его растворимость s(Ag2SO4).
Поскольку из 1 моль Ag2SO4 образуются 2 моль ионов Ag+ и 1 моль ионов , то с(Ag+) = 2s(Ag2SO4), а с( ) = s(Ag2SO4).
3. Найдем искомую растворимость (моль/дм3) соли, подставив в уравнение для ее ПР концентрации ионов, выраженные через s(Ag2SO4):
ПР(Ag2SO4) = с2(Ag+) ∙ с(SO42–) =
= [2s(Ag2SO4)]2 · s(Ag2SO4) = 4s3(Ag2SO4).
Отсюда следует:
s(Ag2SO4)
=
1,6
· 10–2 моль/дм3.
4. Найдем растворимость Ag2SO4 в г/дм3.
Поскольку молярная масса Ag2SO4 равна 312 г/моль, а химическое количество этой соли в растворе объемом 1 дм3 равно 1,6 · 10-2 моль, ее масса равна:
m(Ag2SO4) = 1,6·10–2 моль ∙ 312 г/моль ≈ 5 г.
Следовательно, растворимость сульфата серебра Ag2SO4 составляет 1,6 · 10-2 моль/дм3 или 5 г/дм3.
Пример 1.6.6. Растворимость PbI2 при 20 оС равна 6,5 · 10–4 моль/дм3. Рассчитайте ПР(PbI2) при указанной температуре.
Решение.
1. Напишем схему равновесия между осадком и раствором и выражение для ПР данной соли:
PbI2 (к) ↔ Pb2+(р-р) + 2I–(р-р); ПР(PbI2) = c(Pb2+) ∙ c2(I–).
2. Найдем концентрации ионов в насыщенном растворе соли над ее осадком. Из схемы равновесия видно, что молярная концентрация ионов Pb2+ в растворе соли равна ее растворимости, а концентрация ионов I– – в 2 раза больше:
c(Pb2+) = s(PbI2) = 6,5 · 10–4 моль/дм3;
c(I–) = 2· s(PbI2) = 2 · 6,5 · 10–4 моль/дм3 = 1,3 · 10–3 моль/дм3.
3. Найдем величину ПР(PbI2), подставив в его выражение соответствующие концентрации ионов:
ПР(PbI2) = c(Pb2+) ∙ c2(I–) = 6,5 · 10–4 · (1,3 · 10–3)2 = 1,1 ∙ 10–9.
Пример 1.6.7. Образуется ли осадок Ca3(PO4)2, если к раствору объемом 100 см3 с молярной концентрацией CaCl2, равной 3 · 10–5 моль/дм3 добавить раствор объемом 200 см3 с молярной концентрацией Na3РO4, равной 4,5 · 10–4 моль/дм3? ПР[Ca3(PO4)2] = 2,0 ∙ 10–29.
Решение.
1. Найдем новые молярные концентрации солей в растворе после смешивания исходных растворов. Исходим из простого правила: «Во сколько раз увеличился объем раствора, во столько раз уменьшилась молярная концентрация содержащегося в нем вещества». Математическая зависимость между объемами растворов и концентрациями веществ в них выражается так:
Vисх · cисх = Vнов · cнов,
где Vисх – объем исходного раствора до смешивания; cисх – исходная концентрация вещества в нем; Vнов – объем конечного раствора (после смешивания), cнов – новая концентрация того же вещества в конечном растворе.
В соответствии с этим новые концентрации солей после смешивания растворов составят:
cнов(CaCl2)
=
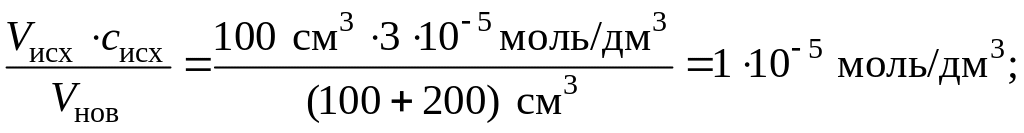
cнов(Na3РO4)
=
2.
Найдем
концентрации ионов Са2+
и
,
образующих осадок, в новом растворе. Из
уравнений диссоциации хлорида кальция
и фосфата натрия
CaCl2 → Са2+ + 2Cl–; Na3РO4 → 3Na+ +
следует, что
снов(Са2+) = снов(CaCl2) = 1 · 10–5 моль/дм3;
снов( ) = снов(Na3РO4) = 3 · 10–4 моль/дм3.
3. Найдем произведение концентраций (ПК) ионов Са2+ и , подставив их в выражение для ПР[Ca3(PO4)2]:
Поскольку ПР[Ca3(PO4)2] = с3нов(Са2+) · с2нов(РO43–), то
ПК =
= (1 · 10–5)3 · (3 · 10–4)2
= 9 · 10–23.
4. Поскольку найденное ПК ионов Са2+ и в новом растворе оказалось больше справочного значения ПР[Ca3(PO4)2], равного 2,0 ∙ 10–29, осадок данной соли при смешивании исходных растворов образуется.
Пример 1.6.8. Сопоставить растворимость (моль/дм3) AgCl при 25 оС в воде и в растворе NaCl, если его молярная концентрация составляет 0,10 моль/дм3, а ПР(AgCl) = 1,8 · 10–10.
Решение.
1. Запишем схему равновесия между осадком AgCl и его насыщенным раствором и выражение для ПР(AgCl):
AgCl(к) ↔ Ag+(р-р) + Cl–(р-р);
ПР(AgCl) = c(Ag+) · c(Cl–).
2. Выразим молярные концентрации ионов Ag+ и Cl– через растворимость s(АgCl) в чистой воде. Из схемы равновесия видно, что:
c(Ag+) = c(Cl–) = s(АgCl).
3. Найдем величину s(АgCl) в чистой воде, подставив в выражение ПР(AgCl) вместо концентраций ионов растворимость s(АgCl):
ПР(AgCl) = c(Ag+) · c(Cl–) = s2(АgCl) = 1,8 · 10–10.
Отсюда находим:
s(АgCl) =
4. Выразим концентрациию ионов c1(Ag+) через растворимость AgCl в растворе NaCl, обозначив ее s1(AgCl). Из схемы равновесия видно, что
c1(Ag+) = s1(AgCl).
5. Выразим концентрациию ионов c1(Cl–) через растворимость AgCl в растворе NaCl. Ионы Cl– образуются как при диссоциации AgCl, так и при диссоциации NaCl. Поскольку растворимость AgCl очень низка, можно пренебречь концентрацией ионов Cl–, образующихся из него, и считать, что все ионы хлора, содержащиеся в растворе, образовались из NaCl. Тогда:
c1(Cl–) = c(Cl–)(из AgCl) + c(Cl–)(из NaCl) ≈ c(Cl–)(из NaCl) ≈ 0,1 моль/дм3.
6. Найдем величину s1(AgCl), подставив в уравнение для ПР(AgCl) концентрации ионов c1(Ag+) и c1(Cl–):
ПР(AgCl) = c1(Ag+) · c1(Cl–); 1,8 · 10–10 ≈ s1(AgCl) · 0,1;
Отсюда находим: s1(AgCl) ≈ 1,8∙10–9.
7. Сравним растворимость AgCl в воде и в растворе NaCl:
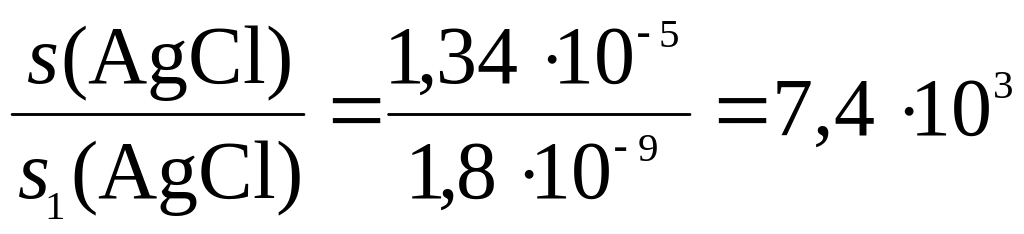раз.
Таким образом, растворимость AgCl в чистой воде больше его растворимости в растворе NaCl с указанной его концентрацией примерно в 7400 раз.