1.2 Прямокутні перерізи з подвійною арматурою
Розміщення робочої (розрахункової) арматури в стиснутій зоні елементів, що зазнають згину, майже завжди викликається необхідністю посилити стиснутий бетон у переармованих перерізах обмеженої висоти або забезпечити тріщиностійкість попередньо напружених елементів під час їх виготовлення, зберігання, транспортування і монтажу.
Іноді можна розрахунком врахувати ту арматуру, яку так чи інакше введено в стиснуту зону перерізу з конструктивних міркувань: пропущені, наприклад, на проміжну опору нижні стержні нерозрізаної балки, армованої в’язаною арматурою (у випадку, коли ці стержні не відгинаються).
Можна вважати, що згинальний момент, який сприймається перерізом з подвійною арматурою, складається з двох доданків
М = М1 + М2,
де М1 – частина момента, який сприймає бетон стиснутої зони і розтягнута арматура Fa1, поставлена за αмакс; М2 – частина момента, яку сприймає арматура пере армування розтягнутої зони Fa2 і така сама за площею арматура F’a = Fa2, розміщена в стиснутій зоні для її підсилення.
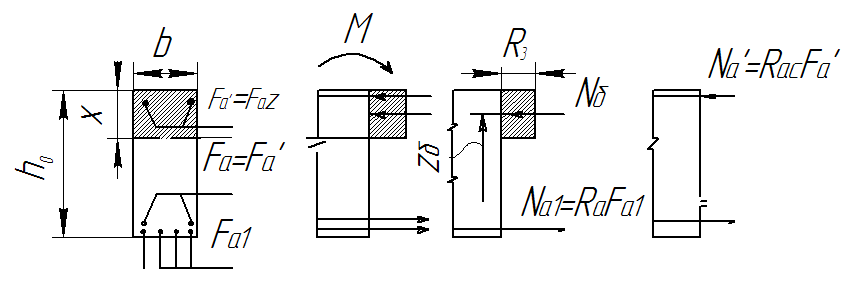
Рисунок 1.2 - До розрахунку прямокутного перерізу з подвійною арматурою
Рівняння рівноваги перерізу, зображеного на рисунку 1.2, набуває такого вигляду
або, після перетворень,аналогічних зображеним у формулах (1.6; 1.7)
(1.11)
Межі використання формули (1.11) такі:
1.
(1.12)
2.
(1.13)
3.
(1.14)
4.
(1.15)
Суть першого обмеження викладеного на стор. 9, друге – обмежує насичення розглянутої зони арматурою з конструктивних міркувань. Суть третього в обмеженні кількості стиснутої арматури з економічних міркувань. Максимальний момент, що його сприймає елемент, який зазнає згину, з подвійною арматурою, не повинен перевищувати максимального момента при одиночному арматуванні того самого елемента більш ніж на 25%
Ммакс < 1,25 R3 ξ S0 ,
звідки для прямокутних перерізів з бетону марки не вище «400» дістають умову (1.14).
Четверте обмеження вказує на те, що стиснуту арматуру слід розмістити досить близько до стиснутої грані перерізу, але без порушення нормальної товщини захисного шару бетону. В противному разі напруги в цій арматурі будуть нижчі від прийнятих в розрахунку і її міцність виявиться невикористаною.
Практичні задачі, які можна розв’язувати за допомогою рівняння (1.11) , ілюструють приклади 2 і 3.
Приклад 2. Підібрати площу перерізу розтягнутої арматури Fa для балки обмеженої висоти, в стиснутій зоні якої є задана арматура перерізом F’а = 4,02 см2.
Дано: розрахунковий згинальний момент М=18100 кгсм; R3=100 кгс/см2;Ra=2700 кгс/см2,розміри перерізу bh =20 50см.
Розрахунок. Згинальний момент, який сприймається стиснутою арматурою і площею перерізу частини розтягнутої арматури, що дорівнює їй, М2 = RaF’a (h0 – a’) = 2700 4,02 (44,5 – 3,5) = 445 000 кгс/см.
Неприйнятна частина момента
Приклад 3. Підібрати мінімальну сумарну площу перерізу розтягнутої і стиснутої арматури в балці прикладу 2.
Розрахунок.
(1.16)
(1.17)
20,1 + 1,98 = 22,08 < 22,84 см2 =18,82 + 4,02.
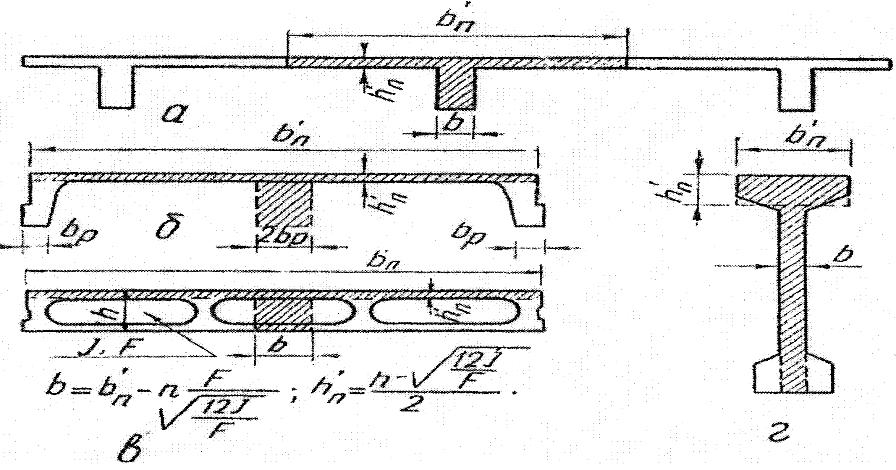
а – таврова балка монолітного перекриття; б – ребриста панель; в – багатопустотна панель (n – кількість пустот, I, F – їх момент інерції і площа перерізу); г – двосхила балка.
Рисунок 1.3 - Різновиди перерізів, розташовуваних як таврові, якщо поличка в стиснутій зоні
Таврові і двотаврові перерізи розраховують, беручи до уваги роботу звисів поличок лише в тому разі, коли останні розташовані в стиснутій зоні. Стиснуті полички таврів або двотаврів, якщо вони монолітно зв’язані з ребрами, дуже впливають на їх несучу здатність і жорсткість посилюючи стиснуту зону. Тому подібні перерізи – балок монолітних і прогонів збірних перекриттів, дво- і односхилих балок покриттів, підкранових балок, ребристих і багатопустотних панелей тощо – застосовують частіше (рисунок 1.3, 1.4).
Однак вплив стиснутих поличок треба обмежувати , нормуючи їх ширину bп’, що вводиться до розрахунку. Інакше переріз може зруйнуватися сколюючими напругами в місці сполучення плит із ребром.
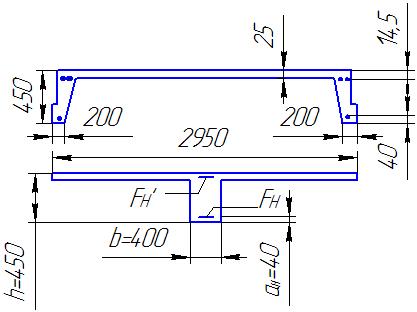
Рисунок 1.4 - Поперечний переріз ребристої плити покриття
Ширина стиснутої полички bп’, що вводиться в розрахункові формули, не повинна перевищувати:
при hп’ < 0,05 h звиси полички в розрахунках не враховуються;
у балках ребристих монолітних покриттів
в усіх випадках
кроку балок, ребер і
прогону балки.
У багатопустотних настилах bп’ приймають рівною ширині настилу, hп’ – товщині стиснутої плити, а ширину ребра еквівалентного (що заміняє) таврового перерізу – сумарній ширині всіх ребер.
При перемінній висоті звисів полички значення hп’ можна вважати рівним середній висоті звисів.
Залежно від положення нейтральної осі розрізняють два випадки розрахунку таврових перерізів:
1-й – з нейтральною віссю в межах товщини полички (рисунок 1.5а.);
2-й – з нейтральною віссю, що пересікає ребро (рисунок1.5б).
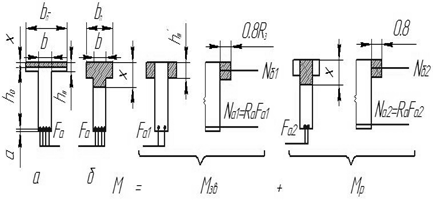
а – за першим випадком; б – за другим випадком
Рисунок 1.5 - До розрахунку таврових перерізів
Розрахункові формули для цих випадків різні, і тому перш ніж починати розрахунок, слід з’ясувати, з яким із них довелося зустрітися.
Це можна зробити, розглянувши окремий
випадок розміщення нейтральної осі по
нижній грані плити для якого
Якщо
,
(1.18)
або
(
)
, (1.19)
А якщо ліві частини нерівностей (1.18) або (1.19) виявляються більшими від правих, то це вказує на 2-й випадок, при якому нейтральна вісь пересікає ребро.
Коли треба визначити висоту стиснутої зони бетону таврового перерізу, розв’язують відносно х одно з рівнянь рівноваги:
якщо припустити, що нейтральна вісь розміщується в поличці, то
(1.20)
а якщо припустити, що нейтральна вісь розміщується в ребрі,
то
(1.21)
У першому випадку (дивитись 1.5 а.) таврові перерізи розраховують за формулами для прямокутних, замінюючи ширину стиснутої зони ребра bп’. Це випливає з тієї розрахункової передумови, що розтягнутий бетон в роботі перерізів участі не бере.
У 2-му випадку (дивитись рисунок 1.5 б) розрахунок ведуть так: обчислюють частину згинального момента, яку сприймають звиси полички і частина розтягнутої арматури:
(1.22)
Відповідний йому переріз частини розтягнутої арматури визначають за формулою, аналогічною формулі 1.9:
(1.23)
Потім знаходять залишковий згинальний момент, який сприймається бетоном ребра (з наявною там арматурою) і рештою розтягнутої арматури
Мр = М – Мзв. (1.24)
За моментом Мр обчислюють коефіцієнт А0, а далі за формулою (1.1.а) знаходять переріз решти арматури Fa2. Повний, сумарний, переріз арматури в розтягнутій зоні
Fa = Fa1 + Fa2. (1.25)
Потрібну площу перерізу повздовжньої не напружуваної арматури в стиснутій зоні визначають за формулою
(1.26)
де А0 макс приймають за табл. 1.1;
(1.27)
(1.28)
Коефіцієнт 0,8 у формулах (1.22), (1.23) і (1.28) приводить згин міцність бетону (Rз) до призмової міцності: Rпр = 0,8 R3, бо поличка цілком (центрально) обтиснута.
Щодо рівняння рівноваги таврового перерізу з нейтральною віссю в ребрі, то після певних перетворень рівняння (1.21) (див. формули 1.15 і 1.11) воно набере такого вигляду
(1.29)
Отже, розрахунковий момент у цьому разі можна подати як суму двох моментів:
Мзв – момента, що сприймається звисами полички і частиною розтягнутої арматури Fа1;
Мр – момента, що сприймається стиснутим бетоном ребра і відповідним перерізом розтягнутої арматури Fа2.
Межі застосовності формул для розрахунку таврових і двотаврових перерізів визначає, як і для прямокутних перерізів, умова (1.3).
Зауважимо, що звиси поличок у розтягнутій зоні під час перевірки цієї умови не враховують; при нейтральній осі в ребрі перевірку умови (1.3) роблять тільки для ребра, без урахування звисів полички.
Переріз арматури в процентах від розрахункового перерізу ребра (bh0) і в таврових балках не повинен бути нижчий від значень, що наводяться в таблиці 1.2.
Приклад 4. Підібрати площу перерізу арматури в прогоні таврової балки, що входить до складу монолітного ребристого покриття.
Дано: розрахунковий загальний момент М– 18 500 кгс м; Rз = 100 кгс/см2; Ra = 2700 кгс/см2; крок балок 2,5 м; розміри перерізу ребра bh – 20 50 см.
Розрахунок. h0 = 50 – 3,5 см = 46,5 см.
За формулою
,
чому в таблиці 1.3 відповідає α = 0,034.
Тоді за формулою (12а)
Оскільки RaFa = 27000 * 14,65 = 39600 кгс < R3b’п h’п = 100 * 8 * 250 = 200 000 кгс, то нейтральна вісь розміщується в поличці, і розрахунок виконано правильно, як для балки прямокутного перерізу шириною b’п = 250 см.
Приклад 5. Підібрати розміри перерізу і одиночне армування таврової збірної балки.
Дано:розрахунковий згинальний момент М=14 500 кгсм; R3 = 100 кгс/см2; арматура класу А – ІІ.
Розрахунок. Прийнявши ширину ребра b =
20 см і розміри полички b’п h’п
= 40 8 см, а також р = 1,8 % для ребра балки,
за формулою (1.1) визначають α = 0,018
.
За ним у табл. 1.3 знаходять r0 = 1,65.
Потім за формулою (1.7) знаходимо
Знаючи h0 приймемо висоту ребра h = 50 см, тоді h0 = 50 – 3,5 = 46,5 см.
Оскільки М = 1 850 000 кгс см > R3b’п h’п (h0 – 0,5 h’п) = 100 · 40 ·8 · (46,5 - 4) = 1 360 000 кгс см, то, виходить, нейтральний шар перерізає ребро балки.
Частина згинального момента, що сприймається звисами полички і частиною перерізу розтягнутої арматури за формулою (1.22)
Мзв = 0,8 ·100 · (40 – 20) · 8 · 42,5 = 545 000 кгс см.,
А за формулою (1.23)
Кільцеві (трубчасті) перерізи. Рівняння рівноваги внутрішніх і зовнішніх зусиль, прикладених до кільцевого перерізу (рисунок 1.6), дістають за тією самою схемою, що й для прямокутних або таврових в перерізів, - сума проекцій всіх сил на повздовжню вісь елемента дорівнює нулю:
, (1.30)
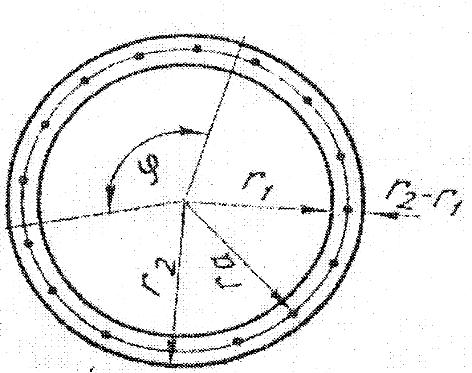
Рис. 1.6 - До розрахунку кільцевих перерізів
а зовнішній розрахунковий момент повинен бути не більший від суми моментів усіх внутрішніх сил відносно осі, що проходить через центр ваги перерізу
(1.31)
Під час написання цих рівнянь зроблено два припущення:
- межа між стиснутою і розтягнутою зонами проходить не по прямій, перпендикулярній до площини дії момента, а по двох радіусах, що утворюють з цією площиною кут φ = παк;
- арматура (не менше шести стержнів) рівномірно розподілена по кільцю, яке проходить через їх центри ваги.
Відстань від рівнодіючої внутрішніх сил у стиснутій зоні бетону, яка має форму частини кільця, до центра ваги перерізу
а відстані від рівнодіючих внутрішніх зусиль у стиснутій і розтягнутій арматурі до центра ваги перерізу дорівнюють
Підставивши їх значення в рівняння (1.31) і (1.32), дістанемо ці рівняння рівноваги в остаточному вигляді
(1.32)
(1.33)
У формулах (1.32) і (1.33)
(1.34)
Значення αк макс, виражені через ξ, такі:
а
)
якщо переріз армовано тільки
напружу-ваною арматурою при
σ0 ≥ 2000 кгс/см2
б) якщо переріз армованого як не напружуваною, так і напружуваною арматурою при σ0 > 2000 кгс/см2
(1.35)
в) якщо переріз армовано як не
напружуваною так і напружуваною
арматурою при
де ξ – коефіцієнт із таблиці 1.1