9.4 Плоско-радіальний потік пружної рідини. Основна формула теорії пружного режиму фільтрації

Розглянемо приплив пружної рідини до точкового стоку (джерела) в необмеженому пласті. Для цього випадку диференціальне рівняння має такий вигляд:

(9.61)

або з урахуванням наявності осьової симетрії (див. підрозд. 4.3)

(9.62)

чи

(9.63)

Нехай задано постійний об’ємний дебіт стоку . Тоді початкова і граничні умови набувають вигляду:

(9.64)

Останню умову конкретизуємо так:

. (9.65)

Задача може бути розв’язана методами Фур’є, операційним. Легко одержується розв’язок на основі аналізу розмірностей. Шуканий тиск залежить від п’яти визначальних параметрів r, t, , р_к , , три з яких мають незалежні розмірності (r, t, р_к).

Тоді безрозмірний тиск залежить від двох безрозмірних комплексів:

. (9.66)

Другий комплекс є постійним параметром. Звідси випливає, що задача автомодельна, оскільки шуканий безрозмірний тиск залежить тільки від однієї змінної , яку для подальшої зручності беремо з числом 2 у знаменнику, тобто

. (9.67)

Тоді аналогічно попередньому рівняння (9.62) зводиться до звичайного диференціального рівняння, а розв’язок задачі зводиться до формули, яку називають основною формулою пружного режиму пласта. Так, для безрозмірного тиску диференціальне рівняння (9.62) запишеться:

(9.68)

Для розв’язування рівняння (9.68), диференціюючи вирази (9.66) і (9.67), знаходимо:

Підставляючи знайдені вирази в рівняння (9.68) і враховуючи, що отримуємо звичайне диференціальне рівняння

або

(9.69)

яке необхідно розв’язати за початкової і граничної умов, які випливають із умов (9.64):

. (9.70)

Використовуючи підстановку , послідовно знаходимо:

(9.71)

де вираз (9.71) – загальний розв’язок рівняння (9.69); – постійні інтегрування.

Постійну знаходимо із граничної умови (9.70), тобто

Постійну знаходимо з використанням початкової умови (9.70), а саме:

звідки розв’язок (9.71) набуває вигляду:

(9.72)

Позначаємо , тоді

,

а розділивши на , маємо

.

Переходячи до розмірного тиску , отримуємо основну формулу пружного режиму:

(9.73)

або

. (9.74)

Інтеграл у формулі (9.73) називається інтегральною показниковою (експоненціальною) функцією, що табульована в довідниках і позначається так:

, (9.75)

де .

Об’ємну витрату рідини через будь-яку поверхню фільтрації з координатою r отримуємо за формулою:

а диференціюючи формулу (9.73), маємо:

або

(9.76)

Для малих значин аргументу , коли , з похибкою до 1% інтегральну показникову функцію можна брати наближено, утримавши перших два члени розкладу функції в ряд:

, (9.77)

де с_е = 0,5772… – постійна Ейлера.

Тоді основну формулу пружного режиму наближено запишемо ще й так:

. (9.78)

Задача 9.1. Свердловину пущено в роботу з постійним дебітом 150 м³/доб в необмеженому пласті, початковий тиск в якому становив 20 МПа. Необхідно визначити тиск на відстані r = 250 м від свердловини через 200 діб. Відомо: коефіцієнт гідропровідності і товщина пласта 10^‑9 м³/(Пас) і 18 м; коефіцієнт пористості пласта 12%; коефіцієнти об’ємної пружності нафти і породи β_н = 2,1·10^‑9 Па^‑1  і β_п = 1,15·10^‑10 Па^-1.

Розв’язування. Визначаємо коефіцієнт об’ємної пружності насиченого пласта:

β^* = β_п + mβ_н = 1,15·10^‑10 + 0,12·2,1·10^‑19 = 3,67·10^-10 Па^-1.

Визначаємо коефіцієнт п’єзопровідності пласта:

κ = м²/с.

Визначаємо тиск у пласті, на відстані 250 м від свердловини:

p(r,t) = 20·10⁶ – 19,37·10⁶ Па.

Відповідь: тиск на відстані 250 м від свердловини через 200 діб її роботи буде становити 19,37 МПа.

Із формули (9.78) маємо похідні по часу t і радіусу r у вигляді:

; (9.79)

, (9.80)

із яких слідує, що темп зміни тиску не залежить від координати r, а градієнт тиску збігається з градієнтом тиску в разі усталеної фільтрації нестисливої рідини (див. підрозд. 4.3). Оскільки у разі усталеної фільтрації

,

то звідси отримуємо рівняння (9.80), тобто

.

Оскільки ці висновки одержано з наближеного запису основної формули, то це означає, що невдовзі після пуску свердловини навколо неї (для ; похибка  1%) тиск розподіляється так, як і в разі усталеної фільтрації за логарифмічною залежністю, тобто тиск у цій зоні виявляється квазіусталеним (від лат. quasi, що означає “немовби”, “ніби”, “несправжній”). У часі розміри цієї зони збільшуються, а поза нею розподіл тиску відрізняється від усталеного розподілу (рис. 9.8).

Основну формулу пружного режиму (9.74) одержано для точкового стоку (радіус ) в необмеженому пласті (радіус ). Аналіз показує, що нею можна з достатньою точністю користуватись як для реальних свердловин (радіуса порядку 0,1 м), так і для так званих “збільшених” свердловин (радіус становить сотні й тисячі метрів), якими подають нафтові поклади в навколишній водонапірній області, а також у пластах, обмеженних розмірів. В.М. Щелкачов встановив, що під час розрахунку тисків на вибоях свердловин радіусів обмеженних розмірів у необмеженому пласті похибка не перевищує 0,6%, коли , а в пласті (відкритому і закритому) обмеженних розмірів не перевищує 1%, коли , , де , – безрозмірні параметри Фур’є, або інакше безрозмірний час; – радіус колового контура живлення (з постійним тиском р_к) скінченного відкритого пласта або радіус кругової непроникної межі закритого пласта обмеженних розмірів.

Наприклад, якщо м²/с; r_c = 0,1м; , то маємо с, тобто через 1 с після пуску свердловини похибка розрахунку вибійного тиску за основною формулою (9.74) не перевищує 0,6%, але надалі зменшується.

Аналогічно, якщо м²/с; r_c = 0,1м; = 10⁴м; Fо = 0,35, то маємо діб, тобто через 405 діб після пуску свердловини в скінченному пласті похибка розрахунку вибійного тиску за основною формулою (9.74) не перевищує 1%, але надалі збільшується.

Якщо , причому тут – зведений радіус свердловини, то одержуємо із формул (9.74) і (9.78) зміну депресії тиску в часі:

; (9.81)

(9.82)

або

, (9.83)

де відповідно

(9.84)

та

. (9.85)

Формулу (9.82) можна інтерпретувати як формулу Дюпюї:

, (9.86)

де радіус контура пласта

. (9.87)

Із рівняння (9.87) випливає, що радіус зони збурення тиску (збуреної області) зростає у часі, а коефіцієнт п’єзопровідності характеризує швидкість поширення збурень тиску в пласті, так як

Задача 9.2. Визначити коефіцієнти гідропровідності та п’єзопровідності пласта за даними зміни тиску на вибої свердловини радіусом 0,1 м після пуску її в роботу з постійним дебітом 75 м³/доб в часі:

Час, год	1	24
Депресія тиску, МПа	0,42	0,515

Розв’язування. Записуємо основну формулу пружного режиму фільтрації для двох змін депресії тиску на вибої свердловини:

Здійснюємо перетворення даних формул, до лінійних рівнянь

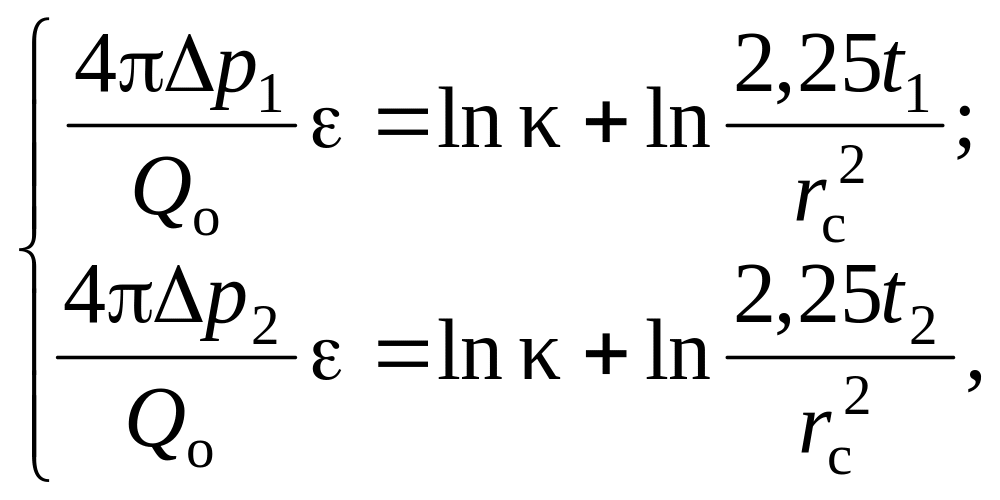
де – коефіцієнт гідропровідності пласта; κ – коефіцієнт п’єзопровідності.

Тоді із системи рівнянь

знаходимо невідомі величини ln(κ) та ε, матричним способом:

; .

Для перемноження матриць використовуємо програму MathCAD:

= ;

отже отримуємо, що lnκ = 0,4456, а коефіцієнт гідропровідності пласта ε = 2,311·10^-9 м³/(Па·с).

Визначаємо коефіцієнт п’єзопровідності пласта: 1,561 м²/с.

Відповідь: ε = 2,311·10^-9 м³/(Па·с); 1,561 м²/с.