Саратовский государственный технический университет

Кафедра: «Электронные приборы и устройства ».

Курс лекций.

Электроника

для студентов

специальности 200700

«Радиотехника».

По направлению 654200

«Электроника и микроэлектроника»

+

курс 2

семестр 4

расчетно-графическая работа (РГР-зачет)

экзамен

зачет

лекции 51

лабораторные работы 34

самостоятельная работа 75

часов в неделю 5

всего 160

Саратов 2013

Лекция 1 Электрофизические свойства радиоматериалов

Материалы, применяемые в электронной технике, подразделяют на радиомате­риалы и конструкционные материалы. Под радиоматериалами понимают мате­риалы, свойства которых зависят от электрических и магнитных полей. Конст­рукционными материалами называют материалы, которые должны обеспечивать механическую прочность изделий, создаваемых из этих материалов. Электричес­кие и механические свойства материалов обусловлены их структурой, которая, в свою очередь, определяется структурой электронных оболочек атомов. По реак­ции на электрическое поле радиоматериалы делят на проводники, диэлектрики и полупроводники. По реакции на магнитное поле различают магнитные и немаг­нитные материалы.

Химическая связь между атомами

Под химической связью понимают взаимодействие между атомами, в результате которого образуются молекулы и твердые тела. Химическая связь осуществляет­ся посредствам электронов, находящихся на внешних, не полностью занятых элек­тронных оболочках. Эти электроны называют валентными. Независимо от при­роды сил, возникающих при сближении частиц, характер взаимодействия между атомами остается одинаковым (рис. 1.1): на относительно больших расстояниях появляются силы притяжения F_пр, быстро увеличивающиеся с уменьшением рас­стояния x между частицами (кривая 1); на небольших расстояниях возникают силы отталкивания F_от, которые с уменьшением расстояния увеличиваются гораз­до быстрее, чем F_пр (кривая 2). На расстоянии x = r₀ силы отталкивания уравнове­шивают силы притяжения и результирующая сила взаимодействия F обращает­ся в нуль (кривая 3). Состояние частиц, сближенных на расстояние r₀, является состоянием равновесия. Существует несколько видов химических связей.

Рис. 1.1

Структура твердых тел

Существуют две разновидности твердых тел: аморфные и кристаллические. Аморф­ные тела характеризуются случайным (хаотическим) расположением частиц (атомов, ионов или молекул). В кристаллических телах частицы расположены строго упорядоченно, на определенном расстоянии друг от друга, образуя про­странственную кристаллическую решетку. Частицы, расположенные в узлах ре­шетки, не могут покидать состояние равновесия, так как при удалении от этих положений появляются силы, стремящиеся вернуть их обратно. Единственной формой движения этих частиц являются беспорядочные колебания около поло­жения равновесия. Энергия каждого такого колебания квантована. Порцию энер­гии тепловых колебаний называют фононом.

Кристаллические тела могут существовать в виде отдельных крупных кристал­лов (монокристаллы) или же состоять из отдельных зерен (поликристаллы). В поликристаллах в пределах каждого зерна частицы расположены периодичес­ки, но при переходе от одного зерна к другому на границах раздела эта периодич­ность нарушается. Монокристаллы обладают анизотропией, то есть их механичес­кие, физические, тепловые и другие свойства различны в разных направлениях. Поликристаллы изотропны, то есть их свойства одинаковы во всех направлениях.

Кристаллические тела состоят из большого числа одинаковых многогранников. Каждый такой многогранник называется элементарной ячейкой кристалла. Эле­ментарные ячейки характеризуются длиной ребер а, b, с, называемых постоян­ными решетки, и углами между ребрами α, β, γ(рис. 1.7). Оси х, у, z, совпадающие с ребрами а, b, с, называются кристаллографическими осями. За начало коорди­нат этих осей выбирают один из узлов решетки.

Рис. 1.7

Если а = b = с и α = β = γ = 90°, то такая решетка называется кубической. Кубические решетки имеют три разновидности. В простой кристаллической решетке (рис. 1.8) восемь атомов расположены в вершинах куба с координатами, указанными в скобках: 1(0,0,0), 2(0,1,0), 3(1,1,0), 4(1,0,0), 5(0,0,1), 6(0,1,1), 7(1,1,1), 8(1,0,1). За единицу в данном случае принята сторона элементарной ячейки. В объемоцентрированной решетке помимо восьми атомов, расположенных в вершинах куба, имеется девятый атом в центре куба с координатами (1/2, 1/2, 1/2). В гранецентрированной решетке атом внутри куба отсутствует, но появляются атомы в центрах всех граней: 9(1/2,0,1/2), 10(1/2,1/2,1), 11(1/2,1,1/2), 12(1/2,1/2,0), 13(1/2, 1/2, 1/2), 14(1, 1/2,1/2).

Рис. 1.8

Кристаллические решетки кремния и германия так же, как и решетка алмаза, со­стоят из двух гранецентрированных решеток, сдвинутых друг относительно дру­га на одну четверть диагонали куба. При определении свойств крис­таллов принято указывать расположение кристаллографических плоскостей и на­правлений, перпендикулярных этим плоскостям. Для этого используют индексы Миллера.

На рис. 1.11 показаны три возможных положения кристаллографических плос­костей, которые обозначаются тремя цифрами, заключенными в круглые скобки.

Плоскость (100) проходит через точку x= 1 и параллельна осям у и z

Рис. 1.11

Плоскость (111) проходит через точки х = 1, у = 1, z = 1. Направления, перпенди­кулярные соответствующим плоскостям, обозначаются тремя цифрами в квадрат­ных скобках: [100], [110], [111]. Направление [100] совпадает с направлением оси х, направление [111] — с диагональю куба.

Основные понятия зонной теории

В изолированном атоме электроны способны занимать лишь дискретные энерге­тические уровни, определяемые силами притяжения к ядру и силами отталкива­ния от других электронов. В твердом теле атомы расположены настолько близко друг к другу, что между ними возникают новые силы взаимодействия — это силы отталкивания между ядрами и между электронами соседних атомов и силы притя­жения между всеми ядрами и всеми электронами. Под действием этих сил энерге­тические состояния в атомах изменяются: энергия одних электронов увеличивает­ся, других — уменьшается. В результате вместо дискретных уровней изолированного атома образуются энергетические зоны, состоящие из очень близко расположен­ных энергетических уровней, плотность которых возрастает по мере удаления от краев зоны по параболическому закону, достигая максимума в середине зоны.

Механизм образования энергетических зон схематически показан на рис. 1.13. По мере сближения атомов (уменьшения расстояний) сначала расщепляются самые высокие энергетические уровни, затем по мере сближения атомов — более низкие.

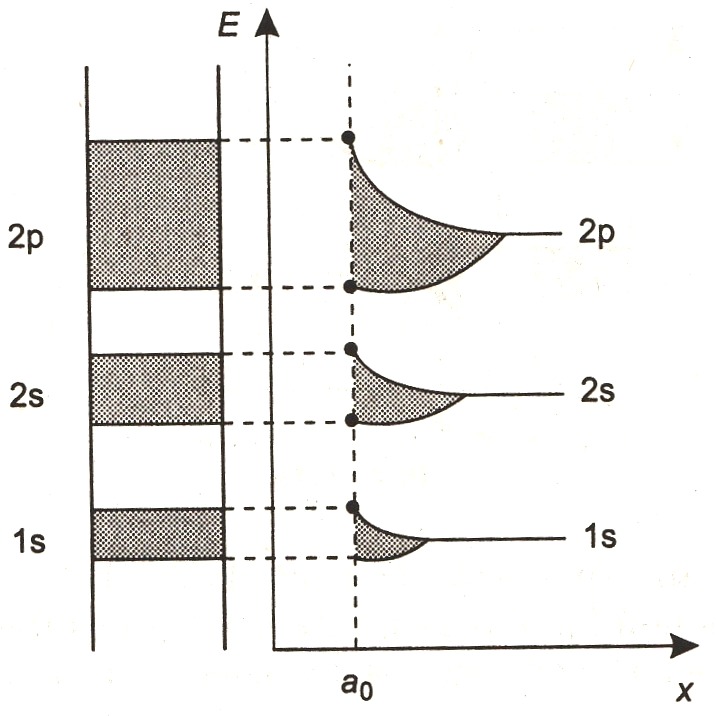
Рис. 1.13

При сближении атомов на расстояние а₀ образуется устойчивая кристаллическая структура, которой соответствует энергетическая диаграмма, показанная в левой части рисунка. Разрешенные зоны отделены друг от друга запрещенными зона­ми, в которых отсутствуют разрешенные уровни. Ширина разрешенных зон по мере перемещения вверх по энергетической шкале возрастает, а ширина запре­щенных зон соответственно уменьшается. Во многих случаях может иметь место перекрытие разрешенных энергетических зон. Подобно энергетическим уров­ням в изолированных атомах энергетические зоны могут быть полностью запол­ненными электронами, частично заполненными и свободными. Все зависит от структуры электронных оболочек изолированных атомов и межатомных рас­стояний в кристалле. Внутренние оболочки изолированных атомов полностью заполнены электронами, поэтому соответствующие им зоны также оказываются заполненными. Самую верхнюю из зон, частично или полностью заполненную электронами, называют валентной зоной, а ближайшую к ней незаполненную элек­тронами — зоной проводимости. Взаимное положение этих зон зависит от струк­туры оболочек изолированных атомов и определяет большинство процессов в твер­дом теле.

Рассмотрим некоторые характерные примеры образования энергетических зон. На рис. 1.14 показана схема образования энергетических зон у лития, изолиро­ванные атомы которого имеют структуру оболочек ls²2s¹. В этом случае зона 2s оказывается заполненной наполовину, поэтому при незначительном внешнем энергетическом воздействии электроны легко переходят на более высокие энер­гетические уровни, что и обусловливает хорошую электропроводность лития. Схожую структуру имеют кристаллы натрия, в которых частично заполненной оказывается зона 3s, и калия, где частично заполнена зона 4s.

Рис. 1.14

1.2. Электрофизические свойства проводниковых материалов

Проводниковыми называют материалы, основным электрическим свойством ко­торых является сильно выраженная электропроводность.

Основные положения классической электронной теории

Хорошая электропроводность проводниковых материалов обусловлена большим количеством свободных (обобществленных) электронов, которые классическая физика рассматривает как электронный газ. В соответствии с этими представле­ниями свободные электроны находятся в состоянии хаотического теплового дви­жения со средней скоростью , сталкиваясь с колеблющимися атомами кристал­лической решетки. Среднее расстояние l, проходимое электроном между двумя столкновениями, называют длиной свободного пробега, средний промежуток вре­мени между двумя столкновениями — временем свободного пробега. Время свобод­ного пробега вычисляется по формуле

Средняя кинетическая энергия электронов, находящихся в непрерывном хаоти­ческом движении, линейно зависит от температуры:

, (1.10)

где k = 1,38·10^-23 Дж/К — постоянная Больцмана. Температуре T= 300К соответ­ствует .

Распределение электронов по энергетическим состояниям, характеризуемое ве­роятностью p(E)), подчиняется статистике Максвелла—Больцмана и описывает­ся экспоненциальной функцией

. (1.11)

При этом считается, что в каждом энергетическом состоянии может находиться любое число электронов, а при температуре абсолютного нуля энергия всех сво­бодных электронов равна нулю.

Если в проводнике существует электрическое поле, то под действием этого поля элек­троны приобретают ускорение, пропорциональное напряженности поля ξ в резуль­тате чего возникает направленное движение электронов со средней скоростью

.

Такое направленное движение называют дрейфом электронов, оно накладывает­ся на хаотическое движение электронов. Скорость дрейфа значительно меньше скорости теплового движения. Направленное движение электронов создает ток, плотность которого равна

, (1.12)

где n — концентрация электронов.

Этот ток пропорционален напряженности поля, коэффициентом пропорциональ­ности является удельная электрическая проводимость

. (1.13)

Классическая теория, давая в целом правильное представление о механизме элект­ропроводности, не учитывает распределение электронов по энергетическим со­стояниям. Поэтому она не может объяснить ряд противоречий теории с опытны­ми данными, в частности, классическая теория не в состоянии объяснить низкую теплоемкость электронного газа. Более полное представление о процессах, про­исходящих внутри вещества, дает современная квантовая физика.

Температурная зависимость электропроводности

В чистых металлах с идеальной кристаллической решеткой единственной причи­ной, ограничивающей длину свободного пробега электронов, являются тепловые колебания атомов в узлах кристаллической решетки, амплитуда которых возрас­тает с ростом температуры. Интенсивность столкновений электронов с атомами, то есть их рассеяние, прямо пропорциональна поперечному сечению сферическо­го объема, занимаемого колеблющимся атомом, и концентрации атомов. Следо­вательно, длина свободного пробега будет равна

. (1.20)

Потенциальная энергия атома, отклонившегося на величину ∆а от узла кристал­лической решетки, определяется соотношением

.

Здесь k_упр — коэффициент упругой связи, которая стремится вернуть атом в по­ложение равновесия.

Поскольку средняя энергия колеблющегося атома равна kТ, то

. (1.21)

Решая (1.21) относительно (∆а)² и подставляя полученный результат в (1.20), определяем среднюю длину свободного пробега электрона:

. (1.22)

Следовательно, удельная электрическая проводимость с ростом температуры уменьшается, а удельное электрическое сопротивление ρ = 1/σ возрастает. Влия­ние температуры на сопротивление проводника оценивают температурным коэф­фициентом удельного сопротивления:

.

У большинства металлов при комнатной температуре α_ρ≈ 0,004 К^-1. Если в метал­ле имеются примеси, то помимо рассеяния на основных атомах возникает рассея­ние электронов на примесных атомах, в результате чего уменьшается длина сво­бодного пробега, определяемая соотношением

.

Здесь l_т и l_п характеризуют рассеяние на тепловых колебаниях основных атомов и примесей соответственно.

Этим объясняется то, что чистые металлы имеют более низкое удельное сопро­тивление по сравнению со сплавами.

Зависимость электропроводности от частоты

На высоких частотах плотность тока изменяется по сечению проводника. Она максимальна на поверхности и убывает по мере проникновения вглубь провод­ника. Это явление называется поверхностным эффектом.

Неравномерное распределение тока объясняется действием магнитного поля тока, протекающего по проводнику. Магнитный поток, сцепленный с проводом, про­порционален току:

,

где L — индуктивность проводника.

Если ток изменяется по синусоидальному закону , то изменение маг­нитного потока вызывает появление ЭДС самоиндукции:

.

Эта ЭДС имеет направление, противоположное току в проводе, и тормозит его изменение в соответствии с законом Ленца.

При прохождении переменного тока переменное магнитное поле возникает как вокруг проводника, так и внутри него. При этом потокосцепление максимально для внутренних слоев и минимально для внешних слоев. Поэтому ЭДС самоин­дукции оказывается максимальной в центре проводника и уменьшается в направ­лении к поверхности. Соответственно, и плотность тока наиболее значительно ослабляется в центральной части проводника и в меньшей степени — у поверхно­сти, иначе говоря, происходит вытеснение тока к поверхности проводника. Оно тем сильнее, чем выше частота.

Распределение плотности тока по сечению проводника подчиняется экспоненци­альному закону:

,

где j₀ — плотность тока на поверхности;

z — расстояние, измеряемое от поверхности;

∆ — глубина проникновения тока.

Глубина проникновения тока, выраженная в миллиметрах, равна расстоянию, на котором плотность тока уменьшается в е =2,72 раз по отношению к своему значе­нию на поверхности проводника. Она пропорциональна удельному сопротивлению ρ [Ом·м] и обратно пропорциональна частоте f[МГц]:

В случае сильно выраженного поверхностного эффекта, когда ток протекает по тонкому поверхностному слою, толщина которого много меньше диаметра про­вода d, экспоненциальное распределение тока может быть заменено однородным распределением с постоянной плотностью тока в пределах тонкого слоя толщи­ной ∆, на основании чего можно ввести понятие эквивалентной площади сечения проводника, занятой током:

.

Поскольку площадь сечения, через которое протекает ток, уменьшилась, то сопро­тивление провода переменному току R_~ стало больше, чем его сопротивление по­стоянному току R₀, что учитывают коэффициентом увеличения сопротивления:

.

Полученная формула справедлива при ∆<<d.

Электропроводность тонких пленок

Электрические свойства тонких пленок отличаются от свойств объемных провод­ников. Это объясняется изменением структуры проводящих пленок и, соответ­ственно, механизма перемещения электрических зарядов, создающих электричес­кий ток. На рис. 1.21 показаны три области, соответствующие трем различным механизмам протекания тока. При напылении пленки сначала образуются отдель­ные разрозненные островки (область 1), переход электронов происходит через узкие диэлектрические зазоры, что обусловлено термоэлектронной эмиссией и туннельным эффектом. В этой области удельное сопротивление очень велико, а температурный коэффициент отрицателен, так как с ростом температуры об­легчается переход электронов от островка к островку.

Рис. 1.21

По мере напыления пленки происходит образование проводящих цепочек между отдельными островками и начинает работать обычный механизм электропровод­ности, удельное сопротивление пленки уменьшается, а температурный коэф­фициент становится положительным (область 2). При дальнейшем напылении островки исчезают и образуется сплошная пленка толщиной около 0,1 мкм (об­ласть 3). На этом участке удельное сопротивление выше, чем удельное сопротив­ление монолитного проводника, что объясняется размерным эффектом, суть ко­торого состоит в сокращении длины свободного пробега электронов вследствие их отражения от поверхности пленки. Полагая, что процессы рассеяния элект­ронов в объеме и на поверхности независимы, можно для длины свободного про­бега l_δ электронов в пленке записать:

.

Здесь l и l_S — длины свободного пробега электронов при рассеянии в объеме и на поверхности.

Приближенно полагая длину свободного пробега при рассеянии на поверхно­сти l_S равной толщине пленки δ, получим:

. (1.23)

Здесь ρ — удельное электрическое сопротивление монолитного проводника. Сопротивление пленки определяется по формуле

где l — длина проводящей пленки;

S — площадь поперечного сечения пленки.

Учитывая, что S = δw, где w — ширина пленки, получаем:

. (1.24)

Здесь - удельное поверхностное сопротивление. Величина ρ_S равна со­противлению пленки при условии l = w, то есть ρ_S представляет собой сопротив­ление пленки, имеющей форму квадрата.

Подбором толщины пленки можно изменять величину ρ_S независимо от удельно­го сопротивления материала.

В микроэлектронике в качестве соединительных пленок применяют пленки из чистого металла, чаще всего алюминия, а в качестве резистивных пленок — туго­плавкие металлы (вольфрам, тантал, рений, хром, молибден) и сплавы никеля с хромом.

Классификация проводниковых материалов

Все проводниковые материалы можно разделить на три основные группы:

• металлы;

• сплавы металлов;

• неметаллические проводящие материалы.

Металлы подразделяют на четыре группы.

• Металлы с высокой удельной проводимостью. К ним относят медь и алюминий, у меди ρ= 0,017 мкОм·м, у алюминия ρ= 0,028 мкОм·м. Это наиболее широко применяемые в электронике металлы. Они применяются для изготовления ра­диомонтажных проводов и кабелей, а также в качестве тонких пленок в интег­ральных микросхемах.

• Благородные металлы. К ним относят золото, серебро, платину и палладий. Они обладают высокой химической стойкостью. Применяются в качестве кон­тактных материалов и коррозиестойких покрытий.

• Тугоплавкие металлы. Эти металлы имеют температуру плавления, превыша­ющую 1700 °С. К ним относят вольфрам, молибден, хром, рений и др.

• Металлы со средним значением температуры плавления. К ним относятся же­лезо, никель и кобальт, обладающие температурой плавления около 1500 °С. Эти металлы имеют сильно выраженные магнитные свойства.

Сплавы металлов подразделяют на три группы:

• Сплавы высокого сопротивления. К ним относят манганин (86 % Cu, 12 % Mn, 2 % Ni), константан (60 % Cr, 40 % Ni), хромоникелевые сплавы. Эти сплавы имеют удельное электрическое сопротивление более 0,4 мкОм·м. Они приме­няются для изготовления резисторов и электронагревательных элементов.

• Сверхпроводящие сплавы. Это сплавы, у которых при температурах, близких к абсолютному нулю, наблюдается резкое уменьшение удельного сопротивле­ния. Среди таких сплавов наилучшими параметрами обладают сплавы ниобия (Nb₃Sn, Nb₃Ga, Nb₃Ge).

• Припои. Это низкотемпературные сплавы, применяемые при пайке. Различа­ют мягкие и твердые припои. Мягкие припои имеют температуру плавления ниже 300 °С. В их состав входит от 10 (ПОС-10) до 90 % (ПОС-90) олова, ос­тальное — свинец. Наиболее распространенными твердыми припоями, имею­щими температуру плавления более 300 °С, являются медно-цинковые (ПМЦ) и серебряные (ПСр).

Неметаллические проводящие материалы подразделяют на три группы:

• Углеродистые материалы. Наиболее широкое применение среди этих материа­лов имеет графит — одна из разновидностей чистого углерода. К ценным свой­ствам графита относятся малое удельное сопротивление и хорошая теплопро­водность, а также стойкость ко многим агрессивным химическим средам.

• Композиционные проводящие материалы. Они представляют собой механичес­кую смесь проводящего наполнителя с диэлектрической связкой. Наибольший интерес представляют контактолы и керметы. Контактолами называют маловяз­кие или пастообразные композиции, применяемые в качестве токопроводящего клея или краски. Связующим веществом в них являются синтетические смолы, а токопроводящим наполнителем — мелкодисперсные порошки метал­лов (серебра, никеля, палладия). Керметами называют металлодиэлектрические композиции с неорганическим связующим веществом. Они обладают вы­соким удельным поверхностным сопротивлением, поэтому применяются для изготовления тонкопленочных резисторов. Наибольшее распространение по­лучила микрокомпозиция Cr-SiO, тонкие пленки которой изготовляют путем напыления в вакууме на диэлектрическую подножку.

• Проводящие материалы на основе окислов. Подавляющее большинство чистых оксидов являются диэлектриками, однако при неполном окислении или при вве­дении примесей проводимость оксидов резко повышается. Такие материалы можно использовать в качестве контактных и резистивных слоев. Практический интерес представляют тонкие пленки диоксида олова SnO₂ и оксида индия In₂O₃.

Лекция 2

Электрофизические свойства диэлектрических материалов

Диэлектриками называют материалы, обладающие незначительной электропро­водностью. Основным электрическим свойством диэлектриков является их спо­собность к поляризации. Под поляризацией диэлектрика понимают процесс упо­рядочения его связанных электрических зарядов под действием электрического поля. Различают несколько механизмов поляризации.

Электронная поляризация

Этот вид поляризации представляет собой упругое смещение и деформацию элект­ронных оболочек атомов и ионов. В чистом виде проявляется в неполярных диэлек­триках, состоящих из электрически нейтральных молекул, у которых центры от­рицательных и положительных зарядов совпадают (полистирол, полиэтилен и др.).

Если такой диэлектрик поместить в электрическое поле между обкладками кон­денсатора, то в каждом из атомов произойдет смещение электронных оболочек относительно своего ядра в сторону положительного электрода (рис. 1.22), в резуль­тате чего образуются упругие диполи, количественно характеризуемые величиной электрического момента m = ql, где l — расстояние между центрами положитель­ного и отрицательного зарядов диполя. Процесс образования упругих диполей протекает практически мгновенно (в течение 10^-14... 10^-16 с) и наблюдается у всех видов диэлектриков.

Рис. 1.22

Величина электрического момента пропорциональна напряженности электричес­кого поля ξ:

.

Здесь α_э— электронная поляризуемость, зависящая от структуры молекулы или атома, Ф·м².

Интенсивность процесса поляризации оценивают величиной электрического мо­мента единицы объема материала:

.

Здесь n — количество частиц в единице объема. Величину Р_др называют поляризованностью диэлектрика. О способности диэлектрика поляризоваться судят по увеличению емкости конденсатора при помещении его между обкладками этого диэлектрика.

При отсутствии диэлектрика (рис. 1.23, а) емкость конденсатора равна

, (1.25)

где ε₀ — абсолютная диэлектрическая проницаемость вакуума (8,84·10^-12 Ф/м);

S — площадь обкладок конденсатора;

d — расстояние между обкладками.

Рис. 1.23

При этом на обкладках конденсатора существуют электрические заряды, величи­на которых равна

.

Здесь U — напряжение между обкладками конденсатора.

При наличии диэлектрика (рис. 1.23, 6) на его поверхности появляются поляри­зационные заряды, а на обкладках конденсатора — наведенные заряды Q_нав, при этом емкость конденсатора возрастает и становится равной

.

Это увеличение емкости учитывают путем введения безразмерного коэффициен­та ε, называемого относительной диэлектрической проницаемостью, который по­казывает, во сколько раз емкость конденсатора с диэлектриком больше емкости конденсатора без диэлектрика. При наличии диэлектрика емкость конденсатора равна

. (1.26)

Для неполярных диэлектриков ε = 2...2,5

Относительная диэлектрическая проницаемость ε и поляризованность Р_др связа­ны между собой соотношением

. (1.27)

Дипольная поляризация

Этот вид поляризации имеет место в полярных диэлектриках, молекулы которых представляют собой твердые диполи (бакелит, целлюлоза, эпоксидная смола), электрические моменты которых ориентированы произвольно (рис. 1.24).

Рис. 1.24

Под воздействием поля эти молекулы частично ориентируются вдоль силовых линий поля, что и является причиной поляризации. Поворот диполей в направ­лении поля связан с преодолением межмолекулярных сил, поэтому протекает сравнительно медленно и сопровождается потерями энергии на нагрев диэлект­рика. После прекращения действия поля ориентированность частиц постепенно ослабевает и поляризованность диэлектрика уменьшается, что может быть запи­сано в виде формулы

,

где P_др(0) — величина поляризованности в момент времени t₀, когда прекращает­ся действие поля;

τ₀ — время релаксации, то есть такой промежуток времени, в течение которого поляризованность уменьшается в е раз (е = 2,71) от первоначального значения.

Процесс дипольной поляризации сопровождается электронной поляризацией, поэтому степень поляризованности полярного диэлектрика оказывается более высокой и ε достигает 6-9.

Ионная поляризация

Этот вид поляризации происходит в кристаллических диэлектриках, имеющих плотную ионную структуру (слюда). Под действием сил внешнего электрического поля в ионных кристаллах происходит упругое смещение ионов отаосительно свое­го первоначального положения (рис. 1.25) на расстояние, меньшее периода решетки.

Рис. 1.25

Смещению ионов препятствуют упругие силы химической связи. В состоянии равновесия действие сил электрического поля уравновешивается действием сил химической связи, то есть

,

где k_упр — коэффициент упругой связи;

∆x — смещение ионов.

Следовательно, величина смещения ионов будет равна

.

Время установления ионной поляризации — порядка 10^-13 с. Величина относи­тельной диэлектрической проницаемости ε составляет 5-12. В ионных диэлект­риках с неплотной упаковкой ионов (органическое стекло и некоторые другие вещества) ионы под воздействием поля смещаются на расстояния, превышающие постоянную решетки. После снятия поля ионы постепенно возвращаются к цент­ру равновесия. Такой вид поляризации называется ионно-релаксационной.

Спонтанная поляризация

Этот вид поляризации имеет место в группе твердых диэлектриков, получивших название сегнетоэлектриков. У таких диэлектриков даже при отсутствии внешнего электрического поля наблюдается самопроизвольная (спонтанная) ориентация твердых диполей в отдельных областях, называемых доменами, линейные разме­ры которых лежат в пределах от 10^-4 до 10^-1 см. В каждом из доменов электричес­кие моменты диполей направлены одинаково, а в разных доменах — по-разному (рис. 1.26, а). Поэтому общий электрический момент сегнетоэлектрика равен нулю.

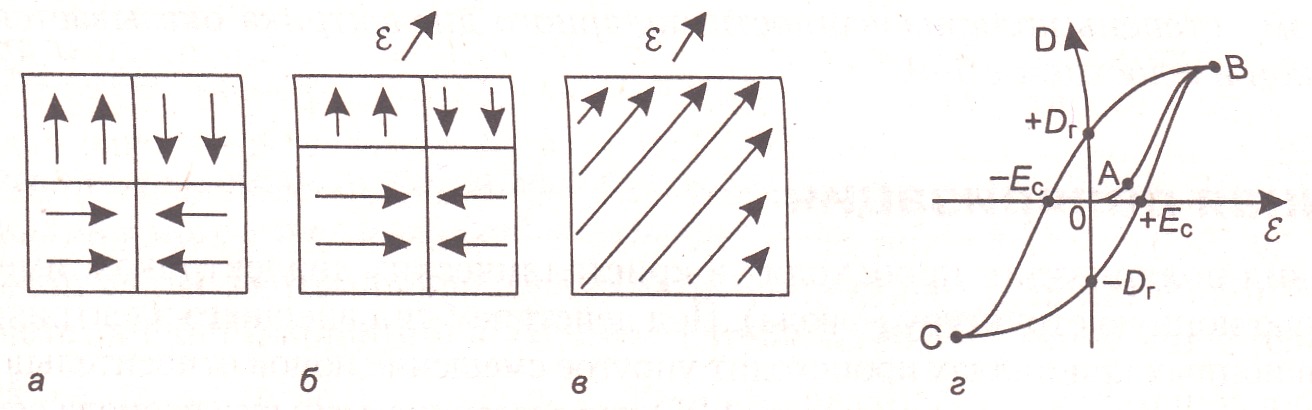
Рис. 1.26

Механизм возникновения спонтанной поляризации можно проследить на приме­ре титаната бария (ВаТiO₃), который по своей научной значимости и техничес­кому применению занимает ведущее место среди сегнетоэлектриков.

При температуре выше 120°С (точка Кюри) титанат бария обладает кристалли­ческой структурой, имеющей форму куба (рис. 1.27).

Если после насыщения напряженность поля уменьшить до нуля, то сохранится вызванная полем ориентация доменов и будет наблюдаться некоторая остаточ­ная индукция D_r. При изменении направления поля происходит переориентация векторов спонтанной поляризации, индукция быстро уменьшается, и при напря­женности –Е_c, называемой коэрцетивной силой, она становится равной нулю. Даль­нейшее увеличение напряженности поля вновь переводит сегнетоэлектрик в со­стояние технического насыщения (точка С).

Таким образом, при поляризации сегнетоэлектриков изменение индукции отстает от изменения напряженности поля. Это явление называется гистерезисом. Площадь петли гистерезиса пропорциональна энергии, затрачиваемой за один период из­менения напряженности электрического поля.

Диэлектрическая проницаемость сегнетоэлектрика определяется по основной кривой поляризации:

.

Влияние температуры на величину диэлектрической проницаемости оценивают температурным коэффициентом диэлектрической проницаемости:

.

Этот коэффициент равен относительному изменению диэлектрической проница­емости при увеличении температуры на 1 °С.

У неполярных диэлектриков диэлектрическая проницаемость слабо уменьшает­ся с ростом температуры (рис. 1.29, кривая 1), так как уменьшается плотность диэлектрика, а следовательно, количество поляризуемых частиц. Величина α_ε от­рицательна, примерно равна коэффициенту линейного расширения диэлектрика и составляет около – 100-10^-6 1/К.

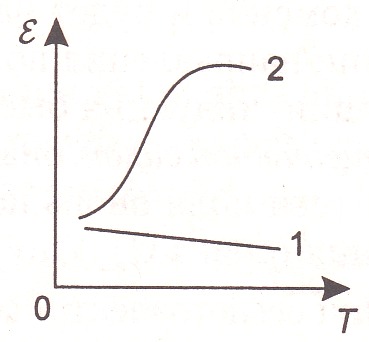
Рис. 1.29

Диэлектрические потери

Диэлектрическими потерями называют мощность, расходуемую электрическим полем на поляризацию диэлектрика. Эта мощность выделяется в виде тепла. По­глощение мощности диэлектриком обусловлено медленными поляризациями и электропроводностью диэлектрика.

Если между обкладками конденсатора помещен неполярный диэлектрик, то пропорционально изменению напряженности электрического поля изменяются элек­трические моменты диполей и, соответственно, электрические заряды, наводимые на обкладках конденсатора, вследствие чего в диэлектрике возникает ток смеще­ния (емкостный ток), пропорциональный скорости изменения напряженности поля:

.

Если напряженность поля изменяется по синусоидальному закону, то

.

При этом I_см опережает приложенное напряжение на угол π/2 (рис. 1.32). Если между обкладками конденсатора помещен полярный диэлектрик, то поворот не­упругих диполей запаздывает относительно изменения напряжения на величину временной релаксации τ0 = 10^-8 с, в результате чего возникающий ток опережает напряжение на угол φ < 90°. Этот ток называется током абсорбции. Таким обра­зом, ток смещения (I_см) обусловлен электронной поляризацией, а ток абсорбции (I_аб) — дипольной. Кроме того, в диэлектрике существует сквозной ток I_ск, совпа­дающий по фазе с приложенным напряжением. Следовательно, полный ток ра­вен I=I_а6 + I_см + I_ск. Активная составляющая такого тока равна I_a = I_ск + I_а.а6, а реак­тивная – I_р=I_см+I_р.аб.

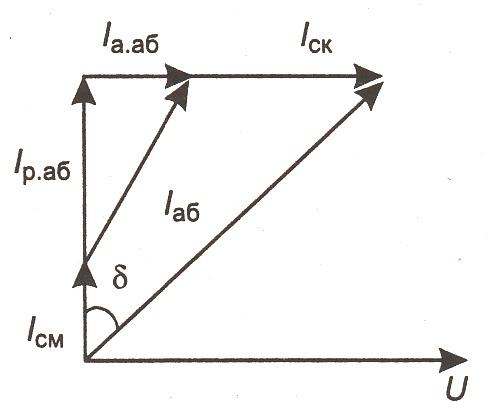
Рис. 1.32

Угол δ, дополняющий до 90° угол фазового сдвига между током и напряжением, называют углом диэлектрических потерь. Тангенс угла диэлектрических потерь, как это следует из векторной диаграммы, можно рассчитать по формуле

.

Из-за наличия тока I_a в диэлектрике выделяется мощность

.

Поскольку , то .

Таким образом, потери энергии в диэлектрике определяются величиной tgδ. У ши­роко применяемых диэлектриков tg δ = (2...5) 10^-3, у высококачественных диэлек­триков tgδ = (2...5) 10^-4.

Электрическая прочность диэлектриков

В нормальных (рабочих) условиях проводимость диэлектриков крайне низка, по­этому их используют как электроизоляционные материалы. Но, находясь в силь­ных электрических полях, при превышении напряжением некоторого критическо­го значения они могут потерять свои электроизоляционные свойства. Это явление называется пробоем диэлектрика. Напряжение, приложенное к диэлектрику и при­водящее к его пробою, называют пробивным напряжением (U_пр), а минимальную напряженность однородного электрического поля, приводящую к пробою диэлек­трика, называют электрической прочностью (ξ_пр):

,

где d_д — толщина диэлектрика.

Существует несколько разновидностей пробоя:

• Электрический пробой возникает тогда, когда некоторое количество носителей зарядов, ускоренных электрическим полем, приобретает энергию, достаточную для ударной ионизации атомов. Это приводит к появлению новых носителей заряда, которые также ускоряются полем, и в итоге возникает лавинообразный процесс увеличения тока, который развивается в течение 10^-7-10^-5 с. Этот про­цесс обычно локализован в узкой области диэлектрика, поэтому следствием его является появление разрядного канала, внутри которого повышается дав­ление, что приводит к появлению трещин или к полному разрушению диэлек­трика. Как правило, этот вид пробоя возникает при ξ_пр = 10³ МВ/м.

• Тепловой пробой возникает тогда, когда количество теплоты, выделяемой в ди­электрике, будет больше количества теплоты, отводимой от него в окружаю­щую среду. В результате происходит нагрев диэлектрика, приводящий к его расплавлению или обугливанию.

• Электрохимический пробой обусловлен медленными изменениями химическо­го состава и структуры диэлектрика, которые развиваются под действием поля или разрядов в окружающей среде.

• При поверхностном пробое пробивается воздух вблизи поверхности твердого диэлектрика, в результате на поверхности образуется проводящий канал. На­пряжение поверхностного пробоя зависит от давления, температуры и влаж­ности воздуха. Для предотвращения поверхностного пробоя поверхность изо­лятора делают ребристой. Эффективной мерой борьбы с данным видом пробоя является замена воздуха жидким диэлектриком.

Лекция 3

Классификация диэлектрических материалов

В РЭА применяют большое количество различных диэлектриков. По функциям, выполняемым в аппаратуре, их подразделяют на электроизоляционные и конден­саторные. Электроизоляционные диэлектрики предназначены для отделения друг от друга элементов схемы и для электрической изоляции токоведущих частей электрических устройств. Они обладают невысокой относительной диэлектрической проницаемостью и большим удельным сопротивлением. Конденсаторные диэлек­трики применяют для увеличения емкости конденсаторов. Эти диэлектрики име­ют повышенное значение е и малое значение tg8. Большое разнообразие диэлект­риков целесообразно классифицировать на основе особенностей их строения.

Полимерные материалы представляют собой высокомолекулярные соедине­ния, молекулы которых состоят из большого числа многократно повторяющихся звеньев (мономеров). В зависимости от пространственной структуры макромоле­кул различают линейные и пространственные полимеры. Макромолекулы линейных полимеров образуют цепочечную последовательность повторяющихся звеньев. Такие полимеры способны размягчаться при нагревании, то есть являются термо­пластичными материалами. Макромолекулы пространственных полимеров раз­виты по всем трем направлениям, образуя пространственную сетку. Такие поли­меры относительно хрупки и при нагревании не размягчаются, то есть являются термореактивными материалами.

Различают неполярные и полярные полимеры. В неполярных полимерах моно­мерные звенья не обладают дипольным моментом. К таким полимерам относятся полиэтилен, полистирол и фторопласт-4, характеризуемые следующими параметра­ми: ε = 2...2,5; tgδ = (2...5)·10^-4; ξ_пр = 20...40 МВ/м; ρ = 10¹⁴...10¹⁶ Ом·м. Из полиэтиле­на изготовляют главным образом гибкую изоляцию высокочастотных проводов и кабелей. Из полистирола изготовляют изоляционные платы и другие радиоде­тали. Тонкие пленки полистирола толщиной 10-100 мкм, называемые стирофлексом, используют в качестве диэлектрика конденсаторов. Фторопласт-4 обладает высокой нагревостойкостью (до +250 °С) и высокой химической стойкостью.

Полярные полимеры обладают сильно выраженной дипольной поляризацией и, следовательно, пониженными электроизоляционными свойствами по сравнению с неполярными полимерами. Они характеризуются следующими параметрами: ε = 3...6; tgδ = 0,01...0,06; ξ_пр = 15...50 МВ/м; ρ = 10¹¹...10¹⁴ Ом·м. Наиболее распрост­раненными материалами этой группы являются поливинилхлорид (ПВХ), полиэтилентерефталат (лавсан) и полиамидные смолы. ПВХ представляет собой жесткий негибкий материал. Для придания эластичности в ПВХ добавляют пла­стификаторы. Такой материал называется пластиком. Он находит применение в производстве монтажных проводов. Пленки из лавсана толщиной около 6,5 мкм применяют в качестве несущей основы при изготовлении лент для магнитной за­писи, а также для межслойной изоляции в обмотках трансформаторов и в каче­стве диэлектрика низкочастотных конденсаторов. Полиамидные смолы отлича­ются высокой механической прочностью и эластичностью. Применяют их для изготовления искусственных волокон (например, капрона) и пластических масс. На основе полиамидов изготавливают эмальлаки, образующие прочные эластич­ные диэлектрические покрытия на металлических проводах.

1.4. Магнитные свойства радиоматериалов

Первопричиной магнитных свойств радиоматериалов являются внутренние скры­тые формы движения электронов. Для объяснения магнитных свойств материалов с достаточным приближением можно пользоваться моделью Бора. При орбиталь­ном движении электронов в атомах возникают орбитальные магнитные моменты, а при вращении электронов вокруг своей оси — спиновые магнитные моменты. Результирующий орбитальный магнитный момент определяют путем суммирова­ния орбитальных магнитных моментов отдельных атомов. У полностью заполнен­ных оболочек он равен нулю. Аналогично определяют результирующий спино­вый магнитный момент, который также равен нулю при полностью заполненных оболочках. Результирующий магнитный момент атома определяется суммирова­нием результирующих орбитальных и спиновых магнитных моментов.

Любой материал, независимо от того, обладают или не обладают атомы материа­ла собственным магнитным моментом, при помещении его в магнитное поле при­обретает некоторый магнитный момент М. Магнитный момент единицы объема материала называют намагниченностью:

.

Намагниченность пропорциональна напряженности магнитного поля H:

,

где k_М — безразмерный коэффициент, характеризующий способность материала намагничиваться в магнитном поле и называемый магнитной восприимчивостью.

Намагниченное тело, находясь во внешнем магнитном поле, создает собственное магнитное поле, которое суммируется с внешним полем. В результате суммарная магнитная индукция становится равной

. (1.29)

Здесь μ₀ = 4π·10^-7 Гн/м – магнитная постоянная, μ — относительная магнитная проницаемость, показываю­щая, во сколько раз магнитная индукция В поля в данном веществе больше, чем магнитная индукция В₀ в вакууме.

По реакции на внешнее магнитное поле все материалы делят на пять групп:

• диамагнетики;

• парамагнетики;

• ферромагнетики;

• антиферромагнетики;

• ферримагнетики.

Диамагнетики — это материалы, атомы которых не обладают собственным магнит­ным моментом. При помещении такого материала в магнитное поле в нем индуци­руется магнитный момент, направленный навстречу направлению поля, поэтому магнитная восприимчивость k_М отрицательна и составляет - (10^-6 – 10^-7). К таким материалам относятся золото, серебро, медь, кремний, германий и ряд других.

Парамагнетики — это материалы, атомы которых обладают собственным магнит­ным моментом. Под действием внешнего поля магнитные моменты атомов ори­ентируются в направлении поля и усиливают его. Магнитная восприимчивость парамагнетиков положительна и составляет 10^-3 – 10^-6. К этим материалам отно­сятся щелочные и щелочноземельные металлы, соли железа, кобальта, никеля и ряд других.

Ферромагнетики — это материалы, в которых атомы, обладающие собственным магнитным моментом, расположены настолько близко друг к другу, что между ними возникает обменное взаимодействие, приводящее к уменьшению энергии системы взаимодействующих атомов. При таком взаимодействии происходит обмен электронами недостроенных внутренних электронных оболочек атомов, в результате чего магнитные моменты взаимодействующих атомов приобретают одинаковое направление. Атомы с одинаковым (параллельным) направлением магнитных моментов группируются в микроскопические области, называемые доменами. Размеры и форма доменов определяются из условия минимума свобод­ной энергии системы. Энергетически выгодна структура с боковыми замыкающи­ми доменами, показанная на рис. 1.35.

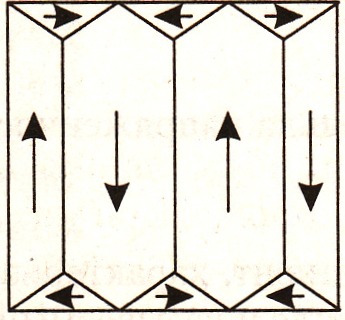
Рис. 1.35

При такой структуре доменов магнитный поток замыкается внутри образца, а за его пределами магнитное поле отсутствует. Под воздействием внешнего магнит­ного поля изменяются размеры и границы доменов и происходит намагничива­ние образца, при этом магнитная восприимчивость достигает 10⁵-10⁶. Подобны­ми свойствами обладают железо, никель, кобальт и некоторые сплавы.

Антиферромагнетики — это материалы, в которых в результате обменного взаимодействия происходит антипараллельная ориентация магнитных моментов ато­мов, поэтому собственный магнитный момент у таких материалов отсутствует. Для антиферромагнетиков характерна невысокая положительная магнитная вос­приимчивость (10^-3 — 10^-5). Антиферромагнетизм обнаружен у хрома, марганца, некоторых редкоземельных элементов и ряда соединений на основе металлов пе­реходных групп.

Ферримагнетики — это материалы, в которых обменное взаимодействие проис­ходит косвенно, через немагнитные ионы кислорода. В результате такого взаимо­действия образуются магнитные моменты, ориентированные в противоположные стороны, но их количество неодинаково, поэтому у ферримагнетиков существует собственный магнитный момент. Подобно ферромагнетикам они обладают вы­сокой магнитной восприимчивостью. Ферримагнетизмом обладают соединения оксида железа (Fe₂О₃) с оксидами других металлов. Примером может служить со­единение оксида железа с оксидом никеля (NiO), называемое ферритом никеля, формула которого может быть записана как NiFe₂О₄.

Намагничивание ферромагнетиков

Если ферромагнетик поместить в магнитное поле, то при увеличении напряжен­ности внешнего поля H можно наблюдать возрастание магнитной индукции В (рис. 1.36), которое обусловлено двумя основными процессами: смещением до­менных границ и поворотом магнитных моментов доменов.

Рис. 1.36

В качестве исходного примем размагниченное состояние ферромагнетика. Этому состоянию соответствует ориентация спинов в доменах, показанная на рис. 1.37, а. При увеличении напряженности поля увеличивается объем тех доменов, магнит­ные моменты которых образуют наименьший угол с направлением внешнего поля (рис. 1.37, б), при этом магнитная восприимчивость не изменяется, а магнитная индукция возрастет пропорционально напряженности поля (участок 1 на рис. 1.36). После снятия поля доменные границы возвращаются в исходное положение.

В области более сильных полей смещение доменных границ носит необратимый характер (рис. 1.37, в). На участке необратимого смещения границ кривая намаг­ничивания имеет наибольшую крутизну (участок 2 на рис. 1.36).

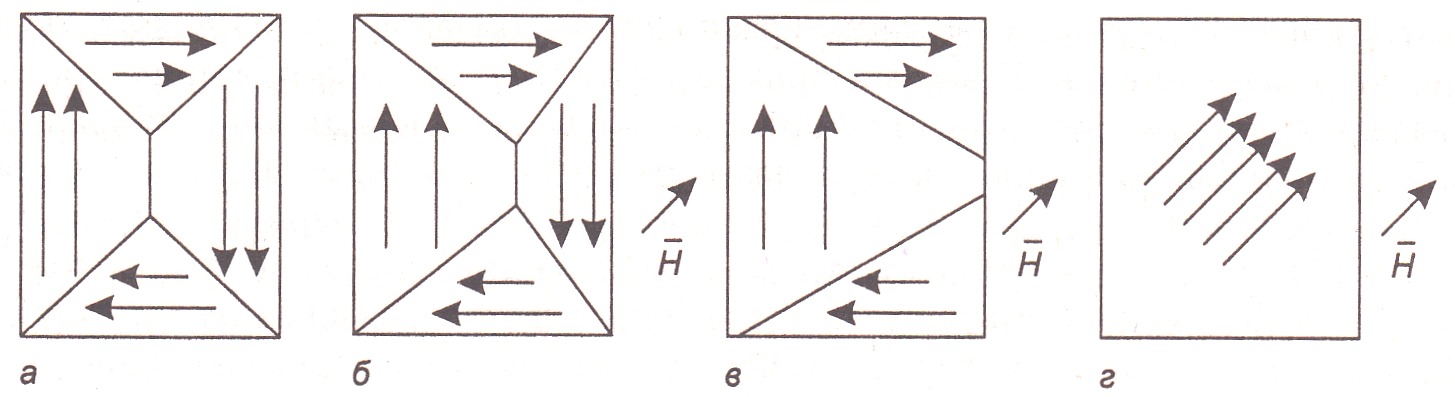
Рис. 1.37

По мере дальнейшего увеличения напряженности поля начинает работать второй механизм намагничивания — происходит поворот магнитных моментов доменов в направлении поля (участок 3 на рис. 1.36). Когда все магнитные моменты доме­нов оказываются сориентированными вдоль поля (рис. 1.37, г), наступает техни­ческое насыщение намагниченности (участок 4 на рис. 1.36). Некоторое увеличе­ние индукции на участке насыщения вызвано слагаемым μ₀H в уравнении (1.29) и увеличением намагниченности самого домена.

Используя кривую намагничивания, можно построить график зависимости маг­нитной проницаемости от напряженности магнитного поля, которая в соответ­ствии с (1.29) равна

.

Магнитная проницаемость μ пропорциональна тангенсу угла наклона прямой линии, проведенной из начала координат через точку на кривой намагничивания. Зависимость проницаемости μ от напряженности поля H показана на рис. 1.38. Значение проницаемости в слабых полях называют начальной магнитной прони­цаемостью (μ_н). Наибольшее значение магнитной проницаемости называют мак­симальной проницаемостью (μ_max).

Рис. 1.38

Если после намагничивания ферромагнетика до насыщения уменьшать напряжен­ность внешнего поля H, то индукция уменьшится, однако она будет больше, чем при начальном намагничивании. На рис. 1.39 представлены зависимости В =f(H) при увеличении и уменьшении напряженности поля; они не тождественны вслед­ствие явления гистерезиса. При уменьшении H до нуля в образце остается оста­точная индукция В_г. Для того чтобы уменьшить индукцию до нуля, необходимо изменить направление поля на противоположное, после чего увеличивать напря­женность поля до величины -H_с, называемой коэрцетивной (задерживающей) си­лой. Если после этого продолжать увеличивать напряженность поля, то ферро­магнетик намагнитится до насыщения -B_s. Изменяя циклически напряженность поля H, можно получить петлю гистерезиса.

Рис. 1.39

Экспериментально установлено, что в монокристаллах ферромагнетиков суще­ствуют направления легкого и трудного намагничивания. Это явление называ­ется магнитной анизотропией. Так, например, у железа, имеющего структуру объемно центрированного куба, направления легкого намагничивания совпада­ют с ребрами куба. Направления трудного намагничивания совпадают с диагона­лями куба. Направления среднего намагничивания совпадают с диагоналями гра­ней куба. У никеля, имеющего структуру гранецентрированного куба, наоборот, ось легкого намагничивания совпадает с диагональю куба, а ось трудного намаг­ничивания — с ребром куба.

При намагничивании ферромагнетиков наблюдается изменение их размеров и формы. Такое явление называется магнитострикцией. Магнитострикцию оценива­ют значением относительной деформации материала в направлении магнитного поля: λ = ∆l/l. Численное значение коэффициента магнитострикции λ зависит от типа структуры, кристаллографического направления, напряженности магнитного поля и температуры. При этом магнитострикция может быть как положительной, так и отрицательной, то есть размеры образца в направлении поля при намагничивании могут как увеличиваться, так и уменьшаться. Так, например, для монокристалла железа, намагниченного в направлении ребра куба, линейные размеры в этом направ­лении уменьшаются, при намагничивании вдоль диагонали куба увеличиваются.

Процесс перемагничивания магнитных материалов в переменном магнитном поле связан с потерями энергии, вызывающими нагрев материала. Эти потери обу­словлены необратимым смещением границ доменов, они пропорциональны пло­щади петли гистерезиса и частоте переменного магнитного поля. Мощность по­терь, расходуемых на гистерезис, определяется формулой

,

где η — коэффициент, зависящий от свойств материала;

B_max— максимальная индукция в течение цикла перемагничивания;

n = 1,6...2,0 — показатель степени, зависящий от В_mах;

f — частота;

V — объем образца.

Помимо потерь на гистерезис перемагничивание магнитного материала сопро­вождается динамическими потерями, обусловленными вихревыми токами, кото­рые магнитный поток индуцирует в магнитном материале. Эти токи возникают в плоскости, перпендикулярной магнитному полю. Мощность потерь на вихревые токи определяется формулой

.

где ξ — коэффициент, зависящий от удельной проводимости, формы и размеров поперечного сечения материала.

Для уменьшения потерь на вихревые токи в трансформаторах применяют сердеч­ники из тонких листов ферромагнитных материалов, изолированных друг от дру­га и обладающих высоким удельным электрическим сопротивлением.