Лекция 8

Тема: Развитие метода комплексных амплитуд

Урок 15. Комплексная форма записи мощности

Рассмотрим способ определения мощности тока цепей в гармоническом режиме при применении метода комплексных амплитуд.

Представим гармонический режим некоторого линейного двухполюсника.

Пусть напряжение цепи имеет комплексную амплитуду

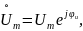
а сила тока имеет ко мплексную амплитуду

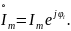
Представим для определенности, что 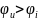, т.е. цепь имеет индуктивную реакцию.

Изобразим режим цепи на векторной диаграмме

На этой диаграмме 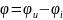– разность фаз напряжений и силы тока.

Спроектируем вектор напряжения на вектор тока.

Разделим вектор 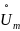на два ортогональных вектора 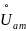и 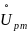. Вектор отображает такое напряжение, которое синфазно силе тока. Это напряжение эквивалентного резистора, входящего в состав двухполюсника. Назовём это напряжение активным. В свою очередь вектор – это вектор напряжения, ортогональный вектору тока. Он описывает напряжение эквивалентного реактивного элемента, т.е. реактивное напряжение.

Разбив общее напряжение двухполюсника на активное и реактивное, мы, тем самым, разделили двухполюсник на два последовательно соединенных идеальных элемента – резистор и реактивный элемент.

Представим это эквивалентными схемами.

Выразим амплитуды активного и реактивного напряжения через амплитуду общего напряжения цепи. Согласно векторной диаграмме

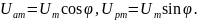
Определим мощность в эквивалентном резисторе и реактивном элементе.

и

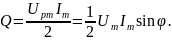
Если бы мы проектировали силу тока на напряжение, получили бы те же самые мощности.

Введем комплексную мощность S таким образом, чтобы действительная часть её совпадала с активной (средней) мощностью, т.е.

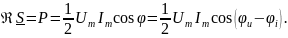
Выразим комплексную мощность через комплексные амплитуды напряжения и силы тока. При этом учтем, что нужно учесть переходы

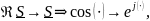
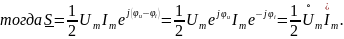
Представим комплексную мощность в алгебраической записи. При этом, учтем, что

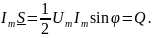
Значит

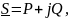
т.е. в одном комплексном числе учтена и активная и реактивная мощность.

Перейдем к экспоненциальной записи мощности.

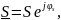
где

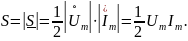
С другой стороны,

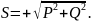
Величину 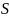называют полной мощностью. Её определяют в вольт-амперах (ВА).

Аргумент комплексной мощности:

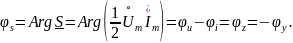
Значит, аргумент комплексной мощности – это разность фаз напряжения и силы тока в цепи, т.е. он совпадает с аргументом комплексного сопротивления цепи.

Расчет режима линейных цепей при действии источников гармонических колебаний с экспоненциально изменяющимися амплитудами

Метод комплексных амплитуд годится не только для исследования гармонического установившегося режима. Его можно применить, если все процессы в цепи относятся к классу собственных или свободных процессов этой цепи. Для линейных цепей это взвешенные суммы колебаний вида

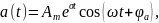
т.е. гармонических колебаний с начальной амплитудой , угловой частотой и начальной фазой 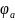. Их амплитуда изменяется во времени по экспоненциальному закону с относительной скоростью .

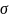Введем комплекс этих колебаний также, как строился комплекс гармонических колебаний, добавляя мнимую часть.

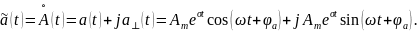
Применяя формулу Эйлера, переходим к экспоненциальной записи

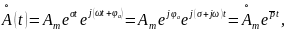
где 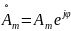– начальная комплексная амплитуда;

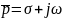– комплексная частота.

Как уже отмечалось, действительная часть комплексной частоты есть относительная скорость изменения амплитуды. При 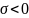это коэффициент затухания колебаний.

Колебания вида 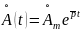называют комплексными экспоненциальными колебаниями.

В частном случае, когда:

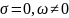1. имеем комплекс незатухающего гармонического колебания

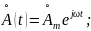
2) 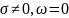получаем экспоненту с действительными значениями

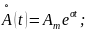
3) 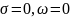получаем функцию-константу

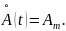
Применяя при расчете комплексные экспоненциальные колебания, мы добиваемся перехода от дифференциальных уравнений к алгебраическим.

Например, при анализе режима последовательной резистивно-индуктивно-емкостной цепи мы получали следующее уравнение:

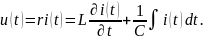
После перехода к комплексным экспоненциальным колебаниям после преобразования получим следующую запись:

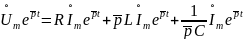
или

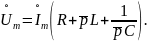
В этой записи

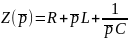– операторное сопротивление цепи, т.е. сопротивление цепи току, сила которого изменяется по косинусоиде с экспоненциально изменяющейся амплитудой.

Соответственно,

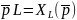– операторное индуктивное сопротивление;

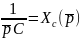– операторное емкостное сопротивление.

Аналогично, можно ввести и операторные проводимости. Все эти операторные величины могут быть получены из комплексных заменой

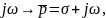
т.е. заменой мнимой частоты 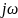на комплексную частоту .

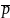Эта комплексная частота, как видно из сравниваемых уравнений, есть один из вариантов записи операторов дифференцирования, т.е.

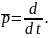
Чтобы пояснить методику расчета линейных цепей, при действии на них процессов из класса собственных, обратимся к примеру.

Пусть к последовательной резистивно-индуктивной цепи подключен источник напряжения, изменяющийся по закону

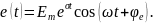
Н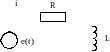 айдем силу тока этой цепи.

Для этого будем считать, что на цепь действует комплексное экспоненциальное колебание.

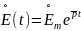
с начальной комплексной амплитудой 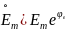и комплексной частотой .

Представим также силу искомого тока цепи в экспоненциальной форме, т.е.

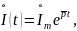
где 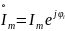– начальная комплексная амплитуда силы тока.

Согласно закону Ома для комплексных амплитуд

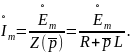
Для нахождения мгновенных значений силы тока 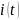представим операторное сопротивление цепи в экспоненциальной форме. Итак,

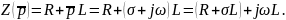
Тогда

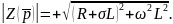
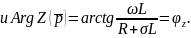
При этом искомая сила тока

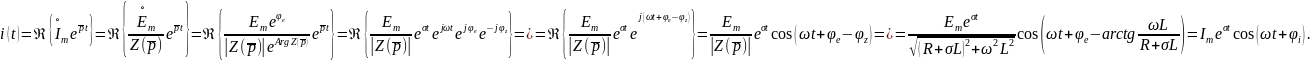
В частности, если

1)

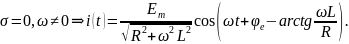
Значит, получили гармонический ток.

2)

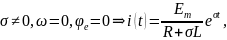
т.е. имеем экспоненциальную реакцию цепи.

3)