Лекция 7

Тема: Примеры расчета режима линейных цепей методом комплексных амплитуд

Урок 13. Гармонический режим последовательной резистивно - индуктивно-ёмкостной цепи

П усть схема замещения цепи имеет вид:

Представим, что через цепь протекает ток силой

комплекс которого и комплексная амплитуда

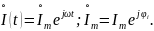
Определим напряжение на всей цепи

имеющее комплекс и комплексную амплитуду

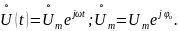
Согласно закону напряжений Кирхгофа

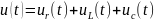
или

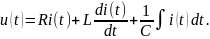
Заменим мгновенные значения процессов их комплексами и произведем необходимые действия над комплексами. Тогда:

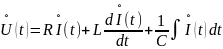
или подробнее,

Сокращая обе части на оператор вращения и вынося за скобки общий сомножитель 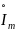, получаем

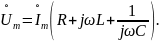
В приведенной записи первое слагаемое в скобках нам известно. Это сопротивление резистора гармоническому току. Значит, остальные слагаемые тоже сопротивления. Соответственно, вся сумма в скобках тоже есть сопротивление. В отличие от ранее рассматривавшихся сопротивлений элементов она есть комплексная величина.

Назовем сумму в скобках комплексным сопротивлением цепи и обозначим как Z.

Итак, комплексное сопротивление

Введя понятие комплексного сопротивления цепи, приходим к следующим простым расчетным формулам:

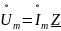или

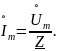
Эти формулы отображают закон Ома в комплексной форме.

Применяя закон Ома, можем определить мгновенное значение искомого напряжения, выполняя п. 4 и п. 5 методики. Тогда

Чтобы получить окончательный результат расчета в наиболее удобном виде, исследуем свойства и формы записи комплексного сопротивления, а также его состав.

Начнем с рассмотрения второго слагаемого. Обозначим его как

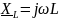
и назовем комплексным индуктивным сопротивлением.

Модуль вводимого сопротивления является известным индуктивным сопротивлением

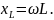
Поэтому

Представим это сопротивление в экспоненциальной форме записи.

Так как, согласно формулам Эйлера:

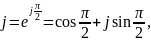
то

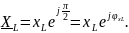
Значит, аргумент комплексного индуктивного сопротивления

Третье слагаемое

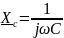
называют комплексным ёмкостным сопротивлением.

Представим его в различных формах записи:

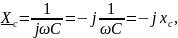
где 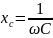– емкостное сопротивление. Это модуль комплексного сопротивления .

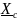С другой стороны

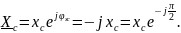
Значит, аргумент

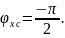
Заметим, что аргументы вводимых комплексных индуктивного и ёмкостного сопротивлений являются упорядоченными разностями фаз между напряжением и силой тока элемента.

Рассмотрим также сумму комплексных сопротивлений реактивных элементов 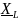и . Тогда:

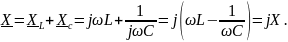
Назовем коэффициент при мнимой единице

реактивным сопротивлением цепи.

Реактивное сопротивление цепи есть действительная величина, которая может принимать различные знаки в зависимости от соотношения сопротивлений реактивных элементов. Введем модуль реактивного сопротивления (и комплексного реактивного сопротивления тоже!)

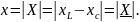
Тогда комплексное сопротивление

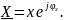
Определим возможные значения аргумента 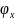. Рассмотрим частные случаи:

1) 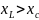, т.е. X > 0 и X = x.

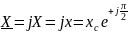Тогда и

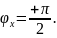
Получился аргумент как у идеального индуктора. Значит, вся реактивная цепь в данном случае есть идеальный индуктор:

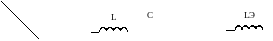
Такой случай называют индуктивной реакцией цепи.

2) 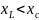, т.е. X < 0 и X =- x.

Тогда и

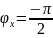
как для идеального конденсатора. Значит, вся реактивная цепь является конденсатором:

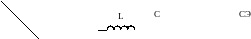
Это – ёмкостная реакция цепи.

3) 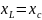, и X = x = 0. В этом случае

и рассматриваемая цепь оказывается резистором.

Такой режим называют резонансом напряжений.

Итак, отмечаем, что комплексное сопротивление цепи

Это алгебраическая запись сопротивления.

Перейдем к экспоненциальной форме записи комплексного сопротивления и установим смысл модуля и аргумента.

Итак,

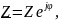
где

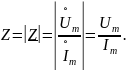
Значит, модуль комплексного сопротивления цепи есть отношение амплитуд напряжения на цепи и силы тока в ней.

С другой стороны

то есть модуль комплексного сопротивления, учитывает сопротивления всех элементов цепи. Его называют полным сопротивлением цепи.

Вычисляем аргумент комплексного сопротивления цепи.

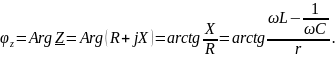
Применяя экспоненциальную запись комплексного сопротивления, можно завершить в наиболее удобном виде вычисление мгновенных значений напряжения последовательной цепи.

Итак,

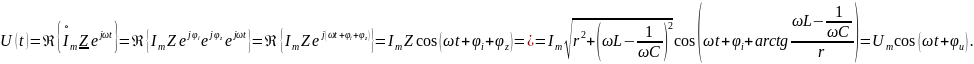
Напряжение тоже есть гармонический процесс. Его амплитуда и начальная фаза зависят от параметров всех элементов цепи.

В общем случае, начальная фаза напряжения

отличается от начальной фазы тока на угол, меньший 90.

Урок 14. Гармонический режим параллельной

резистивно - индуктивно-ёмкостной цепи

Пусть схема замещения цепи есть схема параллельного соединения идеальных линейных резистора, индуктора и конденсатора.

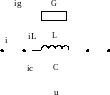
Считаем, что напряжение элементов этой цепи

и значит, комплекс и комплексная амплитуда этого напряжения

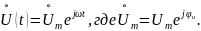
Будем искать силу общего тока цепи.

записав его комплекс и комплексную амплитуду как

Запишем уравнение цепи согласно закону токов Кирхгофа:

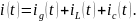
Подставив уравнения элементов, получим

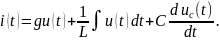
Применяя указанные в уравнении действия над комплексами и комплексными амплитудами, переходим к уравнению

Выделим сомножитель

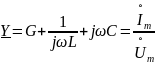
и назовем его комплексной проводимостью цепи. Тогда получим равенства

выражающие закон Ома для комплексных амплитуд.

Применяя закон Ома можно найти мгновенные значения силы общего тока по правилу

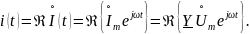
Рассмотрим особенности слагаемых выражения для комплексной проводимости цепи.

Второе слагаемое

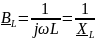
есть комплексная индуктивная проводимость. Представим её в различных формах записи.

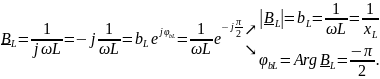
Третье слагаемое есть комплексная емкостная проводимость.

Обозначим её как

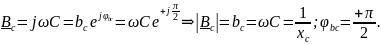
Значит модуль вводимых комплексных проводимостей есть ранее рассмотренные проводимости элементов гармоническому току 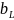и . Значения аргумента этих проводимостей есть упорядоченная разность фаз силы тока и напряжения элемента.

Объединим комплексные проводимости реактивных элементов как комплексную реактивную проводимость

где 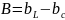– реактивная проводимость цепи.

Представим комплексную реактивную проводимость в экспоненциальном виде:

,

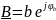где 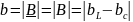– модуль комплексной реактивной проводимости,

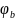– аргумент реактивной проводимости.

Определим возможные значения аргумента .

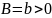1) , т.е. и 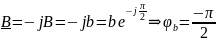, как у индуктора;

Значит, реакция цепи индуктивная:

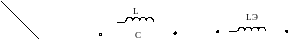
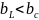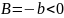2) , т.е. и ;

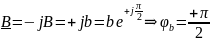Поэтому в данном случае реакция цепи – емкостная.

3) 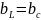, и 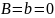. Тогда

Имеем режим резонанса токов.

С учетом введенных проводимостей.

Перейдем к экспоненциальной записи. Согласно закону Ома

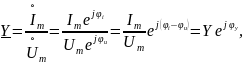
где 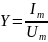–модуль комплексной проводимости цепи;

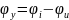– аргумент комплексной проводимости.

Выразим модуль и аргумент через параметры элементов.

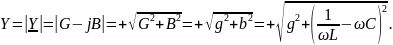
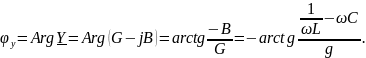
Итак, модуль комплексной проводимости зависит от параметров всех элементов цепи. Его называют полной проводимостью цепи.

Соответственно, аргумент комплексной проводимости:

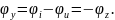
Учитывая экспоненциальную форму записи комплексной проводимости цепи, заканчиваем процедуру нахождения мгновенных значений силы тока параллельной цепи:

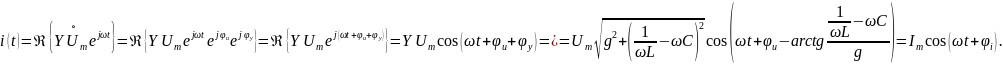
Из приведенных записей видно, что начальная фаза силы тока

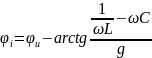
отличается от начальной фазы напряжения на угол, меньший 90.

Связь между сопротивлением и проводимостями двухполюсника

Условия эквивалентности последовательной и параллельной цепей

Пусть мы имеем двухполюсник, комплексное сопротивление которого равно Z.

Представим, что комплексное сопротивление цепи задано в алгебраической форме, т.е.

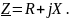
Тогда можно считать, что рассматриваемый двухполюсник есть последовательное соединение – ветвь из резистора с сопротивлением R и реактивного элемента с комплексным сопротивлением jX, т.е.

Найдем комплексную проводимость цепи тоже в алгебраической форме.

где

Значит, активная и реактивная проводимости цепи каждая зависят от активного и реактивного сопротивления.

Полученный результат как алгебраическую сумму проводимостей можно трактовать как проводимость параллельного соединения резистора и реактивного элемента, эквивалентного исходному, последовательному, т.е.

Теперь решим обратную задачу. Пусть в алгебраической форме задана комплексная проводимость некоторого двухполюсника .

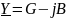Тогда можно считать, что задана схема параллельного соединения резистора с проводимостью G и реактивного элемента с комплексной проводимостью .

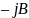Найдем комплексное сопротивление цепи.

где

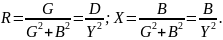
Значит, эквивалентны цепи с такими схемами: