
Лекция 5
Урок 9. Переходный режим линейных динамических цепей второго порядка
Общие положения
Цепи второго порядка содержат два энергоемких элемента разного типа с независимыми режимами. Их переходный режим описывается дифференциальными уравнениями второго порядка, с правой частью.
Решение таких уравнений с равной нулю правой частью – свободная составляющая процессов – есть взвешенная сумма двух экспонент.
Для упрощения расчета принужденной составляющей ограничимся рассмотрением варианта включения в цепь источника постоянного напряжения. В качестве цепи второго порядка примем последовательную цепь из линейных резистора, индуктора и конденсатора.
Включение источника постоянного напряжения на линейную последовательную резистивно-индуктивно-ёмкостную цепь.
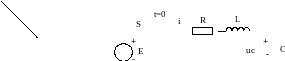
Примем напряжение источника равным Е. Обозначим начальное напряжение предварительно заряженного конденсатора как uc(0) = U.
Определим в переходном режиме мгновенные значения силы тока цепи i и ёмкостного напряжения uc.
Согласно закону напряжений Кирхгофа
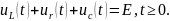
Сначала составим уравнение для нахождения силы тока. Для этого подставим в записанное уравнение уравнения элементов.
Тогда получим уравнение:
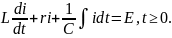
Это интегро-дифференциальное уравнение.
Для получения дифференциального уравнения цепи продифференцируем исходное уравнение и разделим все его члены на индуктивность L.
Тогда будем иметь:
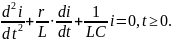
Получилось линейное однородное дифференциальное уравнение второго порядка. Значит, решение уравнения содержит только свободную составляющую. Принужденная составляющая тока отсутствует, т.к. принужденный ток в этой цепи есть ток установившегося режима.
В установившемся режиме, когда t , конденсатор подзаряжается до напряжения источника Е. Поэтому при наличии в цепи двух источников равных, но противоположных напряжений ток должен отсутствовать. Итак, iy = 0 и
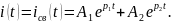
Постоянные А1 и А2 определяются из начальных условий задачи, а именно uc(0) = U и i(0) = 0. Начальный ток в цепи i(0) равен нулю, т.к. в цепи имеется индуктор. Согласно закону коммутации, если до коммутации в цепи ток отсутствует, то, вследствие непрерывности функции индуктивного тока, этот ток должен отсутствовать и в момент коммутации.
Постоянные
p1 и p2
, называемые собственными
частотами цепи, находят путем
подстановки общего решения в
дифференциальное уравнение. При этом
оказывается, что эти постоянные есть
решения алгебраического уравнения,
полученного из дифференциального
уравнения цепи путем замены символа
дифференцирования
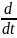 на переменную p, т.е.
на переменную p, т.е.
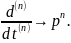
Это уравнение называют характеристическим.
Для нашего примера характеристическое уравнение цепи:
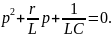
Решения этого уравнения, т.е. собственные частоты:
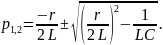
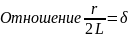 называют коэффициентом затухания,
называют коэффициентом затухания,
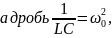
где
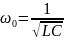 – частота осцилляций.
– частота осцилляций.
С учетом новых обозначений
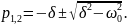
После нахождения значений постоянных А1 и А2 из начальных условий задачи получается результат:
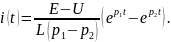
Так как разность собственных частот
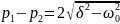
получаем окончательно
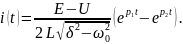
Из представленной формулы видно, что характер переходного режима существенно зависит от соотношения между коэффициентом затухания и частотой осцилляции 0. Поэтому рассмотрим частные случаи для разных вариантов этого соотношения.
Случай большого затухания, когда > 0.
При этом собственные частоты есть отрицательные числа, причем |p2| > |p1|.
Построим график силы тока в цепи, учитывая, что сила тока состоит из двух убывающих экспонент – "медленной" положительной с показателем p1 и "быстрой" отрицательной с показателем p2 , имеющих одинаковые начальные уровни. Примем условие E > U.

Как видно, сила тока не меняет своего направления и имеет максимум.
Построим ещё график ёмкостного напряжения, учитывая, что:
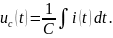
Интегрируя предыдущий график, с учетом начального условия uc(0) = U, получаем зависимость uc(t).
Для случая, когда U < E.

Значит, конденсатор подзаряжается от начального напряжения U до напряжения источника Е. При этом ёмкостное напряжение монотонно возрастает. Точка перегиба зависимости uc(t) соответствует максимуму тока цепи i(t).
Рассматриваемый режим, когда рассматриваемые процессы (переменные состояния) не меняют своего направления с течением времени, называют апериодическим.
Случай малого затухания, когда < 0.
В случае малого затухания собственные частоты оказываются комплексными числами вида:
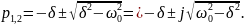
Здесь
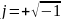 – мнимая единица.
– мнимая единица.
Обозначим
выражение
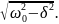 как св и
назовем частотой свободных колебаний.
как св и
назовем частотой свободных колебаний.
Тогда
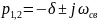 и
и
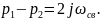
Подставив собственные частоты в общую формулу получим следующее выражение для силы тока:
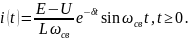
Это гармоничное колебание с экспоненциально изменяющейся амплитудой.
Вычислим емкостное напряжение.
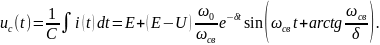
Это
тоже гармоническое колебание с
экспоненциально изменяющейся амплитудой.
Начальная фаза его равна
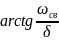 .
.
В отличие от силы тока емкостное напряжение имеет принужденную составляющую :
uс пр = uсу = Е.
Изобразим графики силы тока и емкостного напряжения.
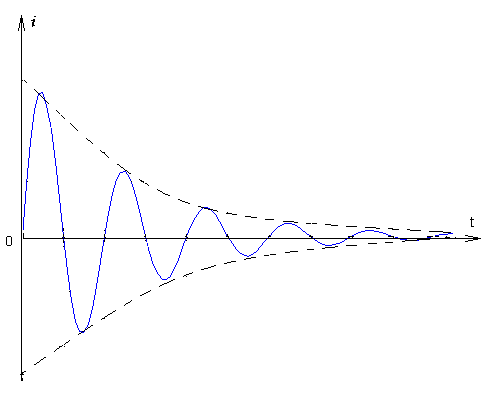
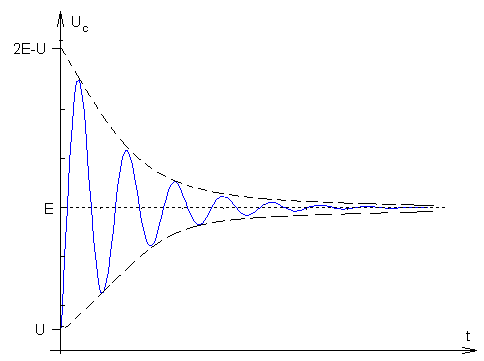
Рассматриваемый режим и процессы при нем называют колебательными. В частности, наблюдается колебательный заряд конденсатора от исходного напряжения U до напряжения источника Е.
Опишем
параметры рассматриваемых колебательных
процессов. Это период колебаний
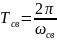 ,
а также относительная скорость снижения
амплитуды , т.е.
коэффициент затухания.
,
а также относительная скорость снижения
амплитуды , т.е.
коэффициент затухания.
Кроме того, для этого вводят декремент колебания.
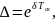
который есть отношение соседних амплитуд процесса через период, и логарифмический декремент
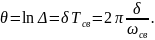
Случай, когда = 0.
В случае, когда = 0 имеем критический режим. В этом режиме графики процессов такие же, как для апериодического режима.
Случай, когда = 0.
В случае, когда =0 и св = 0, т.е. r = 0 и отсутствуют потери в цепи, наблюдаются незатухающие гармонические колебания вида:
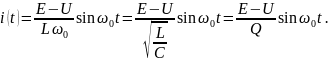
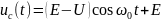
и
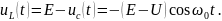
Как
видно из этих формул, частота осцилляции
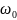 есть частота гармонических незатухающих
колебаний в цепи второго порядка без
потерь.
есть частота гармонических незатухающих
колебаний в цепи второго порядка без
потерь.
Соответственно, параметр
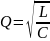
называемый характеристическим сопротивлением цепи, есть сопротивление гармоническому току цепи без потерь.
Введем для цепей второго порядка ещё один важный параметр. Отношение
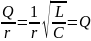
называют добротностью цепи.
Добротность Q связана с коэффициентом затухания и частотой осцилляции соотношением:
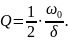
Действительно
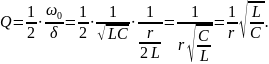
При
апериодическом режиме, когда
> 0,
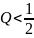 .
.
В
колебательном режиме
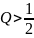 .
.
Урок 10. Метод переменных состояний
Общие положения
Многие радиоэлектронные цепи характерны тем, что в них число энергоемких элементов гораздо меньше общего числа всех элементов. Часто число энергоемких элементов, т.е. порядок цепи, оказывается существенно меньше таких показателей её сложности, как число независимых узлов или контуров.
Если порядок некоторой динамической цепи меньше числа её независимых узлов, то можно ожидать, что в случае, когда за искомые переменные приняты значения процессов, описывающих режим энергоемких элементов, число необходимых уравнений окажется меньшим числа уравнений, необходимых для расчета режима методом узловых напряжений.
Среди переменных, описывающих режим энергоёмких элементов, удобно выбрать в качестве искомых непрерывные процессы, такие, как индуктивные токи iL(t) и емкостные напряжения uc(t). Они, как известно, определяют запасы энергии в цепи, т.е. её энергетическое состояние в любой момент времени. Поэтому их объединяют под названием переменные состояния.
Уравнения цепи, в которых искомыми переменными являются только переменные состояния, называют уравнениями состояния.
Для пояснения процедуры расчетов этим методом, обратимся к примеру расчета цепи второго порядка с двумя независимыми источниками.
Составление уравнения состояния
Изобразим схему линейной динамической цепи:
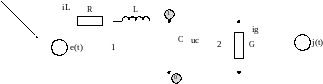
На схеме имеется последовательный резистор с сопротивлением R и резистор, параллельный конденсатору, с проводимостью G.
Вообще
говоря,
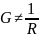 .
.
Выберем в качестве искомых переменных силу индуктивного тока iL и емкостное напряжение uc . Отметим этот выбор на схеме с указанием направления отсчета этих процессов. Укажем также направление тока ig.
Составим систему уравнений цепи по законам Кирхгофа. В качестве независимого узла выберем узел 1. Как независимые контуры выберем соседние ячейки 1 и 2. Тогда получим следующую систему уравнений:
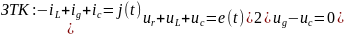
Выразим
все слагаемые в левых частях этих
уравнений через переменные состояния
iL
и uc.
Учтем, что из уравнения 2)
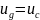 и
и
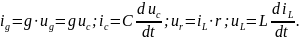
Тогда получаем систему:
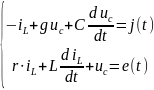
Преобразуем полученное уравнение. Разрешим уравнение относительно производных и упорядочим таким образом, чтобы первой по строкам и столбцам была сила индуктивного тока.
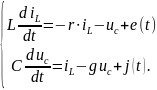
Это и есть уравнения состояния. Каждое из них есть линейное неоднородное дифференциальное уравнение первого порядка. Число уравнений состояния равно порядку цепи, т.е. числу энергоемких элементов с независимыми режимами.
Уравнения состояния могут быть составлены непосредственно по схеме цепи, пропуская этап составления уравнения Кирхгофа.
Для этого разработаны специальные достаточно простые методики.
При
непосредственной записи уравнения
состояния по схеме цепи учитывают, что
в их левой части представлены либо
напряжение индуктора
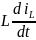 , либо сила тока конденсатора
, либо сила тока конденсатора
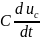 .
Поэтому, при построении уравнений
состояния или ищут напряжения индукторов
.
Поэтому, при построении уравнений
состояния или ищут напряжения индукторов
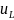 в контурах цепи, или ищут силы тока
конденсаторов
в контурах цепи, или ищут силы тока
конденсаторов
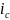 ,
подключенных к её узлам. При этом значения
переменных состояния iL
и uc
считают заданными. Энергоемкие элементы
считают нагрузками, т.е. для них
отождествляют направления напряжения
и силы тока.
,
подключенных к её узлам. При этом значения
переменных состояния iL
и uc
считают заданными. Энергоемкие элементы
считают нагрузками, т.е. для них
отождествляют направления напряжения
и силы тока.
Например,
составим для нашего примера первое из
уравнений состояния с производной
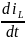 .
.
Для этого выделим левый контур цепи.

Считая известными индуктивный ток iL и емкостное напряжение uc, найдем напряжение индуктора uL из контурного уравнения:
Примем, что направления напряжения uL совпадает с ранее заданным направлением силы тока iL. Тогда:
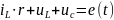
или
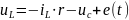 .
.
Правая часть этой записи совпадает с правой частью первого уравнения состояния.
Для
составления второго уравнения с
производной
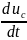 рассмотрим режим узла 1 исходной цепи,
считая известными процессы iL
и uc..
рассмотрим режим узла 1 исходной цепи,
считая известными процессы iL
и uc..
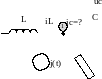
Ищем емкостной ток, считая, что конденсатор заряжается. Составим узловое уравнение.
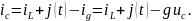
Правая часть этой записи совпадает с правой частью второго уравнения состояния.
Существуют простые и достаточно отработанные алгоритмы решения систем из таких уравнений, когда они представляются в так называемой нормальной форме.
Для перехода к нормальной форме в каждом уравнении все его члены делят на коэффициент при первой производной (т.е. на L или С).
Для нашего примера система уравнений состояния в нормальной форме:
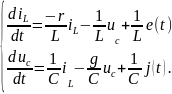
Для решения систем уравнений состояния и получения общих алгоритмов решения, выявления общих закономерностей построения уравнений удобно перейти к их матричной записи.
Матричная запись уравнений состояния
Перепишем уравнения состояния следующим образом:
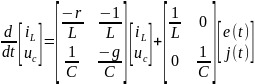
или еще короче:
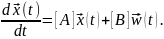
В этих записях:
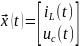 – есть матрица - столбец (или вектор)
переменных состояний цепи;
– есть матрица - столбец (или вектор)
переменных состояний цепи;
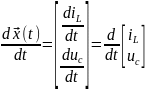 – производная во времени от вектора
переменных состояний;
– производная во времени от вектора
переменных состояний;
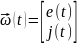 – матрица - столбец (или вектор) процессов
в источниках, иначе матрица
воздействий или матрица
входных переменных (матрица
входов);
– матрица - столбец (или вектор) процессов
в источниках, иначе матрица
воздействий или матрица
входных переменных (матрица
входов);
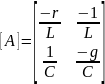 – матрица параметров
пассивных элементов цепи или основная
матрица;
– матрица параметров
пассивных элементов цепи или основная
матрица;
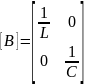 – матрица управления,
т.е.коэффициент, который связывает
значения переменных состояния и входные
переменные e(t)
и j(t).
– матрица управления,
т.е.коэффициент, который связывает
значения переменных состояния и входные
переменные e(t)
и j(t).
В такой общей форме представляются уравнения любых линейных динамических цепей.
Составление и матричная запись выходных уравнений цепи
Если кроме переменных состояния нужно найти мгновенное значение остальных переменных, описывающих режим цепи, то в дополнение к системе уравнений состояния составляют так называемые выходные уравнения.
Вернемся к нашему примеру. Перепишем в несколько иной форме уравнения Кирхгофа.
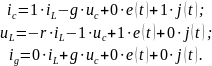
Иными
словами, мы разрешаем уравнения Кирхгофа
относительно множества ещё не найденных
переменных
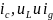 .
.
Эти процессы называют выходными переменными. Кроме того, как при составлении уравнения состояния, слагаемые в правой части этих уравнений выражаем через переменные состояния.
Полученные уравнения для нахождения значений выходных переменных по определенным до этого переменным состояния и заданным воздействиям называют выходными уравнениями.
Выходные уравнения тоже удобно составлять в матричной форме.
Для нашего примера:
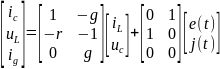
или, короче
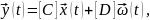
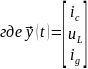 – вектор выходных переменных;
– вектор выходных переменных;
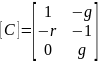 – матрица выхода, т.е. матрица
связи переменных состояния и выходных
переменных;
– матрица выхода, т.е. матрица
связи переменных состояния и выходных
переменных;
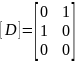 –
матрица входа - выхода, т.е.
матрица непосредственной связи входных
и выходных переменных.
–
матрица входа - выхода, т.е.
матрица непосредственной связи входных
и выходных переменных.
