Лекция № 4

Урок 7. Метод узловых напряжений

Как известно, задача полного анализа режима цепи решается при составлении и решении системы уравнений (контурных и узловых) по законам Кирхгофа. При этом общее число составляемых уравнений должно равняться сумме независимых узлов и контуров. Для сложных многоконтурных цепей с большим числом узлов (а, именно, таковы радиоэлектронные цепи) число составляемых уравнений настолько большое, что это затрудняет вычисления и существенно снижает их точность. Необходим поиск более простых методов расчета, вытекающих из законов Кирхгофа.

Среди более простых, инженерных методов полного анализа режима цепи выделяют методы контурных токов и узловых напряжений.

Остановимся на рассмотрении метода узловых напряжений как наиболее удобного, универсального и чаще применяемого. Метод контурных токов вы изучите дома.

Идея и особенности метода узловых напряжений следующие:

1. ограничиваются составлением узловых напряжений по ЗТК;

2. в качестве неизвестных принимают так называемые узловые напряжения;

3. силы токов цепей записывают как произведение напряжений на проводимости элементов.

Кроме того, для упрощения расчетов, заменяют все источники на источники токов.

Узловыми напряжениями называют разности потенциалов между независимыми узлами цепи и одним и тем же заранее выбранным зависимым узлом, называемым базисным или, короче, базисом.

Потенциал базисного узла принимается нулевым. Тогда узловое напряжение совпадает с предполагаемым потенциалом независимого узла.

Направления узловых напряжений – от независимого узла к базисному.

При расчете напряжения между независимыми узлами выражают через узловые.

С применением метода узловых напряжений (или узловых потенциалов) число составляемых уравнений равно числу независимых узлов. Чем сложнее цепь, тем больше в ней элементов и чем сложнее её структура, тем меньше число уравнений метода узловых напряжений по сравнению с числом уравнений, составляемым по обоим законам Кирхгофа.

Чтобы отличать ранее рассмотренную методику составления уравнений по обоим законам Кирхгофа от метода узловых напряжений, первый из упомянутых называют методом токов ветвей.

Для иллюстрации методики обратимся к конкретному примеру.

Опишем режим резистивной линейной мостовой цепи с источником тока j.

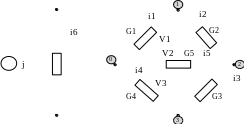
На этой схеме для удобства обозначены не сопротивления, а проводимости элементов.

В качестве базиса принят узел 0. Узловые напряжения выделены стрелками и обозначены как V₁, V₂, V₃. Направления узловых напряжений приняты от независимых узлов 1, 2, 3 к базисному с номером 0.

Для обоснования методики и для уяснения связи её с методом токов ветвей составим уравнения по ЗТК, выражая токи ветвей через проводимости и напряжения их элементов.

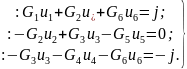
Выразим все записанные напряжения элементов через узловые напряжения. Чтобы выделить узловые напряжения от других, обозначим их буквой V.

Как видно из схемы:

u₁ = V₁; u₅ = –V₂; u₄ = –V₃.

Остальные напряжения, как напряжения на ветвях, расположенных между независимыми узлами, есть разности узловых напряжений (потенциалов узлов) т.е.:

u₂ = V₁ – V₂; u₃ = V₂ – V₃; u₆ = V₁ – V₃.

При составлении этих разностей учтено, что направления отсчетов напряжений элементов совпадают с направлением отсчета тока в них. Кроме того, учтено, что ток течет от точки с более высоким потенциалом к точке цепи с низким потенциалом. Поэтому падения напряжения на пассивных элементах имеют направление от узла с более высоким потенциалом. Значит это упорядоченная разность более высокого и низкого потенциалов, т.е. узловых напряжений.

Поэтому, считаем, что V₁ > V₂, а V₂ > V₃ и, значит, V₁ > V₃.

Итак, при записи напряжений элементов как разности узловых напряжений нужно следовать правилу:

Как уменьшаемое всегда пишут напряжение узла, от которого течет ток (т.е. от которого направлена стрелка отсчета тока).

Подставив выражения для напряжений элементов в исходные уравнения, получим систему:

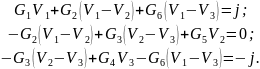
Объединив коэффициенты при узловых напряжениях, получим:

Это система уравнений относительно узловых напряжений – основные уравнения метода.

Перейдем к матричной записи полученных уравнений.

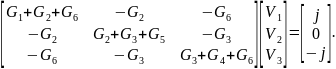
Здесь первый сомножитель – квадратная матрица, каждый размер которой равен числу независимых узлов. Каждый элемент этой матрицы есть некоторая проводимость. Поэтому данную матрицу обозначают как 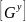и называют матрицей узловых проводимостей.

Второй сомножитель есть матрица-столбец (или вектор), составленный из искомых узловых напряжений. Обозначим его как 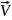и назовем вектором узловых напряжений.

В правой части матричной записи имеется вектор задающих токов источников, подключенных к независимым узлам. Обозначим его как .

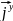Если к некоторому независимому узлу подключен не один, а несколько источников тока, то соответствующий элемент вектора задающих токов записывают как алгебраическую сумму сил токов всех источников, подключенных к узлу. При этом силу задающих токов, протекающих к узлу, записывают со знаком "+". Среди слагаемых пишут и токи "бывших" источников напряжения, предварительно преобразованных в эквивалентные источники тока.

В сокращенной записи уравнения узловых напряжений выглядят следующим образом:

.

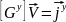Эта запись выражает закон Ома в матричной форме.

Рассмотрим структуру матрицы узловых проводимостей.

Обозначим её элементы как 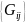, где i – номер строки, а j – номер столбца.

1. Сначала рассмотрим элементы матрицы, находящиеся на её главной диагонали, т.е. элементы из множества 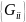. Как видно, при описании линейной цепи, каждый из этих диагональных элементов положителен, т.е. G_ii > 0. Кроме того, каждый диагональный элемент есть сумма проводимостей всех пассивных элементов, подключенных к i-тому независимому узлу.

Такие элементы матрицы называют собственными или полными проводимостями узлов (точнее, это проводимости звезд из пассивных элементов, подключенных к независимым узлам).

2. Теперь заметим, что все внедиагональные элементы матрицы, т.е. элементы из множества , где i  j, отрицательны и совпадают по модулю с проводимостью ветви, включенной между i– ым и j- ым узлами. Их называют взаимными проводимостями узлов или проводимостями связи между узлами i и j.

3. Для цепей с независимо действующими источниками, к которым относится и исследуемая цепь, матрица узловых проводимостей симметричная, т.е. G_ij = G_ji.

Учитывая отмеченные свойства, можно составлять необходимые матрицы непосредственно по схеме цепи, без дополнительных преобразований из уравнений Кирхгофа. Следовательно, процедура составления уравнений по методу узловых напряжений не сложнее методики составления уравнений по методу токов ветвей.

Как нетрудно заметить, число уравнений, которые мы составили по методу узловых напряжений, вдвое меньше, чем число уравнений, которые необходимо составить при непосредственном применении законов Кирхгофа для нахождения шести сил токов в ветвях. Для более сложных цепей этот разрыв ещё больше.

Заметим также, что полученная матричная запись основных уравнений метода универсальна. Она пригодна для расчета режима любых линейных цепей, в том числе и динамических. В этом ещё одно преимущество метода узловых напряжений.

Рассмотрим процедуру расчета методом узловых напряжений путем составления уравнений по схеме цепи.

1. На схеме цепи выделяют базисный узел и направляют к нему стрелки узловых напряжений от независимых узлов. Источники напряжения заменяют на эквивалентные источники тока. Отмечают на схеме проводимости элементов.

2. Формируют по схеме замещения цепи матрицу узловых проводимостей , а также векторы и . Составляют основное уравнение вида .

3. Ищут узловое напряжение с помощью матричной формулы: 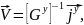в которой 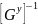– матрица, обратная матрице узловых проводимостей.

4. По найденному множеству узловых напряжений в случае необходимости ищут остальные напряжения, а также силы токов элементов, применяя любой подходящий метод расчета.

Тема: Анализ цепей во временной области

Урок 8. Переходный режим линейных электрических цепей первого порядка

Общие свойства

Анализ цепей во временной области – это нахождение мгновенных значений реакций цепи по заданным мгновенным значениям воздействия (сигналов).

Будем рассматривать особенности переходного режима линейных динамических цепей.

Переходный режим – это режим цепи после очередной коммутации, вызвавшей скачкообразное изменение силы тока или напряжения на исследуемой цепи. Например, такой коммутацией является включение или выключение одного или нескольких источников в цепи.

Динамической называют цепь, содержащую энергоёмкие элементы. В переходном режиме энергоемкие элементы электрической цепи способны стать дополнительными источниками кроме "настоящих", независимых источников напряжения и тока. Эту особенность необходимо учитывать при расчетах.

Как известно, электрический режим линейных динамических цепей описывают линейными интегро-дифференциальными уравнениями.

При наличии в цепи независимых источников эти уравнения являются неоднородными, т.е. в правой части этих уравнений после знака равенства записывают процессы в источниках.

Итак, исследовать режим динамической цепи во временной области – это решить систему интегро-дифференциальных уравнений.

Сложность решения этой задачи зависит от числа и порядка уравнений цепи.

Порядок дифференциального уравнения, которым описывают режим, это один из показателей сложности цепи. Если порядок уравнения равен n, то цепь называют цепью n-го порядка. В ней содержатся n энергоемких элементов с независимыми режимами.

Как известно из курса высшей математики, общее решение линейного неоднородного уравнения независимо от его порядка состоит из двух слагаемых. Одно из слагаемых решения – это частное решение уравнения при заданной правой части. Другое слагаемое – это общее решение однородного уравнения, получаемого из заданного неоднородного приравниванием нулю его правой части.

Если принять правую часть дифференциального уравнения цепи равной нулю, это означает, что мы пренебрегаем действием независимых источников, имеющихся в цепи. Поэтому соответствующее слагаемое общего решения называют свободной составляющей искомых процессов. Соответственно, другое слагаемое – частное решение уравнения для заданной правой части, т.е. для заданных процессов в источниках, называют принужденной составляющей процессов.

Значит, всякий процесс в переходном режиме линейной динамической цепи есть сумма свободной и принужденной составляющей.

Форма, зависимость от времени свободной составляющей процессов зависит от числа электроемких элементов в цепи, её порядка. Доказано, что свободная составляющая процессов в любой цепи n- го порядка есть взвешенная сумма экспонент.

Характер принужденной составляющей определяется процессами в источниках. Если процессы в источниках входят в класс собственных процессов линейной цепи, то закон изменения во времени принужденной составляющей совпадает с законом изменения значений сигналов источников. К классу собственных процессов относятся, например, постоянные силы тока и напряжения или гармонические процессы.

Для указанных примеров, когда процессы в источниках – периодические, принужденная составляющая реакции может существовать, как и воздействия, неограниченно долго. С другой стороны, свободная составляющая, которую создают "внутренние источники", т.е. энергоемкие элементы, практически длится конечное время, т.к. запас энергии тока этих элементов всегда ограничен.

Время существования свободной составляющей – это время существования переходного режима. После этого в реакции цепи остается одна принужденная составляющая и цепь переходит в установившийся режим.

Переходный режим цепей первого порядка

Цепи первого порядка содержат единственный энергоемкий элемент – индуктор или конденсатор. Уравнения описывающие их режим, есть линейные неоднородные дифференциальные уравнения первого порядка вида:

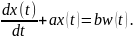
В этой записи

x(t) – искомый процесс;

w(t) – процесс в источнике;

а и b – постоянные коэффициенты.

Общее решение этого уравнения как сумма свободной и принужденной составляющей

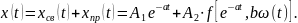
Форма свободной составляющей заранее известна. Это – экспонента, коэффициент в показателе которой совпадает с параметром уравнения (–а). Главная трудность при вычислениях – определение принужденных составляющих. Чтобы её обойти, будем далее считать, что сигнал (t) входит в класс собственных процессов рассматриваемых цепей.

Наиболее просто представляется принужденная составляющая, когда источник – это коммутируемый источник постоянного напряжения или тока.

Тогда

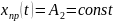
и общее решение имеет вид:

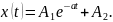
Установим конкретный смысл коэффициентов, входящих в полученную формулу. Для этого определим установившееся значение искомого процесса:

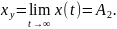
Укажем также начальное значение процесса:

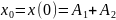, откуда

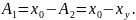
Параметр (–а) описывает особенности состава элементов цепи. Его называют собственной частотой цепи и обозначают также как 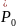. Размерность собственной частоты – .

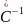Кроме того, в расчетах применяют коэффициент

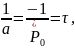
который называют постоянной времени цепи.

С учетом изложенного, универсальная расчетная формула для исследования переходного режима линейных цепей первого порядка имеет вид:

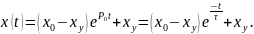
Чтобы пояснить особенности расчета по этой формуле, перейдем к конкретному примеру.

Включение в последовательную резистивно-емкостную цепь источника постоянного напряжения

Представим следующую схему замещения цепи:

Пусть в цепи имеются последовательно соединенные резистор R и конденсатор С. Конденсатор заряжен в указанной полярности.

Представим, что в момент t = 0 к цепи подключается источник с постоянным напряжением Е. Напряжение на заряженном конденсаторе в этот момент примем равным U.

Исследуем переходный режим. Найдем мгновенные значения емкостного напряжения и других процессов в цепи.

По закону напряжения Кирхгофа для всех моментов времени после коммутации

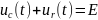при t  0.

Выразим напряжение резистора u_r через напряжение конденсатора. При этом учтем, что через резистор протекает емкостный ток вида:

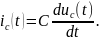
Тогда получаем уравнение:

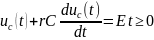
или

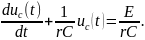
Получилось, как и ожидали, линейное неоднородное дифференциальное уравнение первого порядка.

Его коэффициенты:

собственная частота

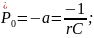
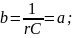
постоянная времени

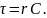
Определим значения остальных постоянных.

Начальное значение емкостного напряжения 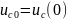задано и равна U.

Так как при подключении источника постоянного напряжения конденсатор подзаряжается, то его напряжение неизбежно сравнивается по модулю и знаку (направлению) с напряжением источника Е, т.е. U_су = Е.

При этом, в цепи окажется два источника с одинаковыми и противоположными напряжениями, отчего ток в цепи исчезнет, и мы перейдем в установившейся режим.

С учетом значений коэффициентов:

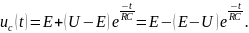
Тогда

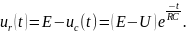
и

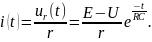
Построим графики переходных процессов. Их называют временными диаграммами.

Рассмотрим случай, когда U < E.

Представленные графики иллюстрируют процесс подзаряда конденсатора от напряжения U до напряжения Е.

Как видно из графиков, параметр , имеющий размерность времени есть точка, в которой сходятся все касательные к процессам для начального момента времени.

Этот параметр, т.е. постоянная времени , есть удобная величина для оценки времени практического существования переходного режима. Обычно это время определяют как:

t_пер = (3…5) .

При этом учитывают, что за промежуток времени 3 всякий убывающий процесс достигает значения 5% от исходного уровня, а при t=5 это значение – 0,7%. При этом возрастающие процессы достигают уровня 95% … 99,3%. Т.е. все процессы практически устанавливаются.