1. Свойство пропорциональности

При изменении всех воздействий цепи в k раз, все реакции цепи изменяются в k раз.

Благодаря этому свойству, можно считать, что вид, форма отклика линейной цепи определены только формой воздействия, но не зависит от их уровня.

На свойстве пропорциональности базируется один из основных методов расчета линейных цепей – метод пропорциональных величин.

2. Свойство наложения (Принцип суперпозиции)

Реакция линейной цепи на сумму воздействий есть сумма реакций на каждое воздействие в отдельности.

Это свойство используют в так называемом методе наложения. По этому методу последовательно находят реакции цепи на действие отдельных источников, а затем получившиеся реакции складывают и получают, тем самым, реакцию линейной цепи на все воздействия.

3. Свойство обратимости (взаимности)

При изменении направления передачи сигнала на обратное, результаты расчета реакции на действие его источников совпадают.

i₂

i₁ = i₂

u₁ = u₂

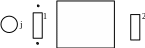
u₂

Основные теоремы линейной теории цепи

Рассматриваем основные теоремы, базирующиеся на основных законах теории цепей с учетом свойств линейных цепей.

Теорема об эквивалентном генераторе

Эта теорема применяется для расчетов режимов цепи в случаях, когда интересуются только двумя величинами: напряжением между заданной парой узлов и/или силой тока, протекающего через эти узлы.

В таком случае цепь мысленно разбивают относительно заданных узлов на два двухполюсника: активный, называемый далее эквивалентным генератором, и пассивный, считающийся нагрузкой этого генератора.

Прежде, чем формулировать теорему, введем некоторые новые понятия, касающиеся режима активных двухполюсников, т.е. генераторов.

Режим, когда генератор отключен от нагрузки, называют холостым ходом.

Случай, когда к генератору подключен идеальный проводник, это – короткое замыкание.

Введем также понятие эквивалентности схем замещения электрических цепей.

Множество схем замещения считают эквивалентными, если с их применением расчет одного и того же участка цепи дает одинаковые результаты.

При рассмотрении теоремы ограничимся наиболее простым вариантом для случая, когда рассматриваемые цепи – резистивные.

Теорема об эквивалентном генераторе имеет две эквивалентные формулировки.

Теорема об эквивалентном генераторе напряжения (Теорема Тевенена).

Схема любого активного линейного двухполюсника эквивалентна схеме Тевенена с задающим напряжением источника, равным напряжению холостого тока этого двухполюсника, и внутренним сопротивлением, равным отношению напряжения холостого тока к току короткого замыкания, т.е.

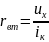
Сущность теоремы можно пояснить схематически. Пусть двухполюсник А есть эквивалентный генератор, а двухполюсник П – его нагрузка, тогда эквивалентная схема:

Так как схема пассивной резистивной цепи может быть эквивалентными преобразованиями сведена к одному резистору R_н , при применении теоремы Тевенена любая сколь угодно сложная линейная резистивная цепь может быть представлена простой одноконтурной трехэлементной цепью. При этом напряжение между выделенными узлами и сила тока, протекающего через эти узлы будут одинаковы для сравниваемых схем.

Теорема об эквивалентном генераторе тока (Теорема Нортона)

Схема любого активного линейного двухполюсника эквивалентна схеме Нортона, с силой задающего тока источника, равной силе тока короткого замыкания этого двухполюсника, а внутренняя проводимость равна отношению силы тока короткого замыкания к напряжению холостого хода, т.е.

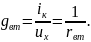
Суть теоремы поясним графически:

Мы не будем доказывать эти теоремы. Эти утверждения становятся очевидными, если учесть, что ВАХ активных линейных двухполюсников представляются прямыми линиями, напряжение u_х = е, а сила тока i_к = j, отчего внутреннее сопротивление

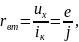что и должно быть для генераторов с линейной ВАХ.

Следствием из теоремы об эквивалентном генераторе является еще одна теорема под названием:

Теорема о преобразовании схем генераторов (Теорема об эквивалентности "реальных" источников напряжения и тока)

Формулировка этой теоремы:

Схема Тевенена и схема Нортона линейно активного двухполюсника эквивалентны, если внутренние сопротивления в сравниваемых схемах одинаковы, а задающее напряжение источника в схеме Тевенена е связано с задающим токов источника в схеме Нортона j соотношением:

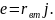
Это соотношение было получено нами ранее, при рассмотрении генераторов с линеаризированными ВАХ. Так что доказывать здесь нечего. Заметим ещё, что по смыслу

e = u_х, j = i_к.