Лекция № 2

Урок 3. Энергоемкие элементы. Накопители электромагнитного поля

Идеальный конденсатор

Конденсатором называют элемент электрической цепи, предназначенный для накопления электрического поля.

Если по сравнению со способностью накапливать, концентрировать электрическое поле можно пренебречь другими свойствами. то приходим к физической модели под названием идеальный конденсатор.

Идеальным конденсатором называют воображаемый элемент, поведение которого исчерпывающим образом описывается функциональной связью между зарядом и напряжением:

F(q, u) = 0.

Это уравнение есть вольт-кулонная характеристика (ВКХ).

И зобразим графики ВКХ идеальных конденсаторов.

Прямая 1 – это график ВКХ линейного конденсатора.

Его уравнение

q – Cu = 0, при С > 0.

Соответственно, кривая 2 представляет ВКХ нелинейного конденсатора.

Л инейный конденсатор обозначается на схемах следующим образом:

Коэффициент 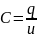называют ёмкостью конденсатора.

Установим единицу этой физической величины:

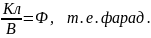При известной ёмкости конденсатора можно полностью описать его электрический режим. Например, сила тока конденсатора

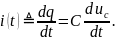
Значит, сила тока, протекающая через конденсатор, тем больше, чем выше скорость изменения напряжения. Если напряжение u_c неизменно, т.е. u_с = 0, то i_c  0. В этом случае конденсатор становится изолятором.

При известной силе тока напряжение конденсатора

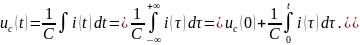
Мощность тока конденсатора:

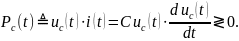
Так как сомножители этой формулы – знакопеременные величины, мощность тока конденсатора может быть и положительной, и отрицательной. Значит конденсатор может быть либо нагрузкой, либо источником в цепи.

Ищем энергию тока конденсатора:

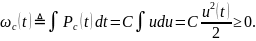
Перейдем к рассмотрению нелинейных конденсаторов.

Обозначение нелинейного конденсатора:

Введем дифференциальную ёмкость по правилу

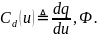
Если задана дифференциальная емкость, то ВКХ

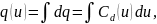
а сила тока конденсатора

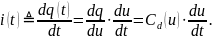
Эта формула аналогична той, что писали для линейного конденсатора.

Для линейного элемента:

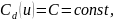
и сила тока представляется частной известной формулой:

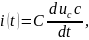
Идеальный индуктор

В электрических цепях применяют катушки индуктивности для накопления магнитного поля. В случае, когда способность к накоплению магнитного поля оказывается определяющей, свойства катушек индуктивности описывают, введя понятие «идеальный индуктор».

Идеальным индуктором называют воображаемый элемент, поведение которого исчерпывающим образом описывается функциональной связью между силой тока и потокосцеплением вида:

F(, i) = 0

где 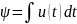– потокосцепление, характеристика интенсивности магнитного поля. Другое название –вольт-секундная площадь (ВСП).

Функция F(, i) – вебер-амперная характеристика (ВбАХ).

Приведем графики возможных ВбАХ.

Прямая 1 – график ВбАХ линейного индуктора.

Его уравнение:

 - L_i = 0

В этом уравнении

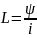
есть индуктивность. Единица индуктивности:

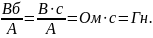
О

L

бозначение линейного индуктора

u

i

При известной индуктивности напряжение индуктора:

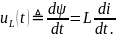
Этой формулой описывается закон электромагнитной индукции М. Фарадея. Напряжение индуктора тем больше, чем быстрее меняется сила тока. Если i(t) = const, то u_L(t)  0, то есть элемент является проводником.

Обратная зависимость:

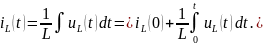
Мгновенная мощность тока в индуктивном элементе:

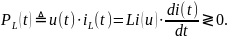
Значит, индуктор может быть не только нагрузкой, но и источником.

Энергия тока элемента:

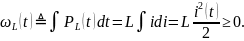
Перейдем к рассмотрению нелинейных индукторов.

Обозначение нелинейного индуктора:

Дифференциальная индуктивность:

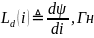
тогда вебер-амперная характеристика

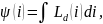
а напряжение индуктора

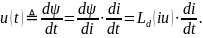
Для линейных индукторов

L_d(i) = L = const.

Законы коммутации

Законы коммутации выделяют множество процессов, изменяющихся непрерывно при скачкообразном изменении других процессов из-за изменения состава и структуры цепи.

Первый закон коммутации или закон непрерывности индуктивного тока

Если напряжение на идеальном линейном индукторе изменяется скачками, то сила тока индуктора изменяется непрерывно.

Второй закон коммутации или закон непрерывности емкостного напряжения

Если сила тока идеального линейного конденсатора изменяется скачками, то напряжение конденсатора изменяется непрерывно.

Непрерывно изменяющиеся процессы i_L(t) и u_c(t), как мы нашли недавно, определяют энергию конденсатора и индуктора, т.е. энергию поля накопленного цепью к моменту времени t. Говорят, что они определяют энергетическое состояние цепи.

Индуктивный ток и емкостное напряжение называют переменными состояния.

Дуальность идеальных элементов и их параметров

Сведем полученные уравнения идеальных элементов в таблицу.

Элемент	Уравнение
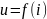
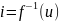
Резистор	u=ir	i=qu	p=i2r=u2q
Индуктор
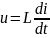
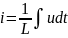
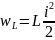
Конденсатор
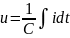
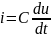
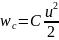
Источник напряжения	u = const	-	p = ui
Источник тока	-	i = const	p = ui

Как видно, уравнения, записанные в этой таблице, имеют пары, отличающиеся только обозначениями.

Пары уравнений (формул), переходящих друг в друга при взаимной замене обозначений, называют дуальными. При этом элементы, описываемые дуальными формулами, также называют дуальными.

Например, дуальны конденсатор и индуктор, источник напряжения и источник тока. Резистор самодуален.

Обозначения и параметры, при замене которых друг на друга получают дуальные формулы, также называют дуальными. Можно выделить такие дуальные пары параметров:

u  i, L  C, r  q, w_L  w_c и т.д.

Свойство дуальности распространяется и на цепи. Его будем использовать для упрощения анализа различных цепей.

Урок 4. Элементы электрических цепей. Схемы замещения

Понятие схемы замещения

Вводимые в теории цепей идеальные элементы (абстрактные элементы) являются физическими моделями реальных элементов, компонентов цепи, предназначенными отражать только одно, определяющее их свойство.

В действительности каждый элемент обладает множеством свойств и параметров, он имеет электрическое поле и магнитное поле. Ток элемента преобразуется в другие формы движения материи. Говорят, что при этом происходят потери энергии электрической цепи.

Для учета всевозможных свойств реальных элементов в самых различных условиях их применения, эти элементы отображают схематически, соединяя друг с другом различными способами обозначения идеальных элементов, описывающих по одному свойству. Такие схемы, составленные из условных графических обозначений (УГО) идеальных элементов, называют схемами замещения.

Соединяя друг с другом схемы замещения элементов, получают схему замещения всей электрической цепи.

Представление элементов цепи их схемами замещения неоднозначно. Выбор вариантов схемы замещения зависит от многих факторов, в том числе от условий применения элементов. Схемы замещения элементов цепи с перечнем условий их применения содержатся в специальных справочниках.

Чтобы пояснить, что такое схемы замещения, обратимся к конкретным примерам.

Схемы замещения катушки индуктивности

Пусть имеется катушка индуктивности, т.е. несколько витков из хорошего проводника не некотором диэлектрическом или ферромагнитном основании (сердечнике). Примерный чертеж катушки индуктивности таков:

Представим, что эта катушка используется в разных режимах.

1. Например, она включена в цепь с постоянным током. Тогда нет необходимости учитывать факт существования постоянного магнитного и электрического поля. Достаточно учесть потери, изобразив идеальный резистор:

2. Пусть катушка со значительной индуктивностью (с большим числом витков) включается в цепь переменного гармонического тока промышленной частоты (50 Гц, 100 Гц, 400 Гц). Тогда придется учитывать явление самоиндукции, добавив в схему замещения катушки идеальный индуктор. Например, сделать так:

3. Для гармонических колебаний радиочастотного диапазона (например, сотни килогерц, единицы мегагерц и т.п.) при описании электрического режима катушки придется учесть тот факт, что часть тока проходит через пространство между витками. Для этого в схему замещения вводят идеальный конденсатор таким образом:

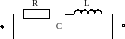
4. В диапазоне сверхвысоких частот большая часть тока катушки проходит не по проводнику, а мимо его. Поэтому схема замещения катушки есть идеальный конденсатор.

Схемы замещения реальных источников (генераторов)

Ограничимся рассмотрением схемных моделей реальных источников с линеаризированной вольт-амперной характеристикой.

Дело в том, что при изменении режима генератора в достаточно малых пределах его характеристику можно аппроксимировать прямой, довольно близко к реальной зависимости, и считать, что ВАХ генератора прямолинейная.

Отразим особенности генераторов графически.

На графике сплошной линией показана ВАХ генератора, а штриховой прямой – её аппроксимация. Представим, что ВАХ и приближающая её прямая пересекают оси в одних и тех же точках. Выделим координаты точек пересечения с осями и примем их за параметры генераторов.

Координату точки пересечения с осью напряжений обозначим как е и назовем задающим напряжением генератора. Соответственно, координата точки пересечения с осью сил токов обозначена как (-j). При этом параметр j называют задающим током источников. Другие наименования: напряжение холостого хода u_х = е и сила тока короткого замыкания i_х = j .

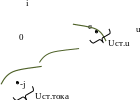
Запишем уравнение прямолинейной ВАХ через введенные параметры. Воспользуемся уравнением прямой в отрезках:

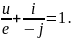
Чтобы получить конкретные варианты схем замещения, разрешим записанное уравнение относительно силы тока или напряжения.

При разрешении уравнения относительно текущего напряжения получаем следующий вариант:

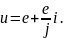
Отношение

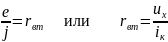
называют внутренним сопротивлением.

Введя обозначение r_вт , получим окончательно:

u = e + r_вт i.

И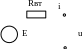 зобразим схему замещения, соответствующую записанному уравнению. В ней должны быть последовательно соединены идеальный источник с напряжением е и резистор сопротивлением r_вт.

Данную схему замещения называют схемой Тевенена. В отечественной литературе её зовут «Схемой реального источника напряжения». Это вызвано тем, что это, в первом приближении, схема замещения электрических машин, в том числе электромашинных генераторов.

Разрешив уравнение в отрезках относительно силы тока, имеем:

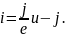
Этому уравнению соответствует схема замещения из параллельно соединенных источника, сила тока которого равна j и резистора проводимостью

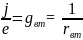
называемой внутренней проводимостью.

С введением внутренней проводимости уравнение генератора принимает вид:

i = g_вт u – j,

а схема замещения становится такой:

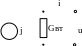
Это – схема Нортона или схема «реального источника тока».

Видимо, возникает вопрос, а как выбрать нужную схему замещения из предложенных?

В том случае, когда при изменении силы отдаваемого генератором тока напряжение генератора изменяется в относительно небольших пределах относительно заданного е, т.е. используется значительно малая, практически линейная часть ВАХ генератора около точки с координатами (е, 0), применяют схему Тевенена. Как уже упоминалось, это схема замещения электромагнитных генераторов или, например, электрических аккумуляторов, и , вообще, источников питания радиоэлектронной аппаратуры.

Указанные условия выполняются, когда внутреннее сопротивление генератора существенно меньше сопротивлений ожидаемых нагрузок, т.е. r_вт <<R_н.

Наоборот, схему Нортона применяют, когда при изменении напряжения генератора его сила тока меняется относительно задающего тока j мало, т.е. используется малая часть ВАХ генератора около точки с координатами (0, -j). Это бывает, когда сопротивление генератора существенно превышает сопротивление его нагрузки, т.е. r_вт >>R_к. Такой особенностью обладают многие источники сигналов в радиоэлектронных цепях.

Сравнивая схемы Тевенена и Нортона одного и того же генератора, получаем вывод (теорема о преобразовании схем источников) о принадлежности этих схем одному генератору.

В схемах Тевенена и Нортона одного и того же генератора внутренние сопротивления одинаковы, а задающее напряжение и задающий ток связаны соотношением:

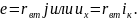
Кусочно-линейная схема замещения полупроводниковых диодов

Как уже отмечалось, в радиоэлектронной аппаратуре широко применяют полупроводниковые диоды. Типовая ВАХ такого диода имеет следующий вид:

Для получения схемы замещения заменим вольт-амперную характеристику двумя лучами, исходящими из начала координат, достаточно близкими в определенном смысле к этой характеристике. Эти лучи выделены штрихами.

Каждый из двух лучей можно считать частью ВАХ идеального резистора. При этом луч в первом квадранте, т.е. в области сильных прямых токов, соответствует линейному резистору с малым прямым сопротивлением r. Луч в третьем квадранте описывает обратный ток. Соответствующее ему сопротивление называют обратным. Обозначим его как R. При этом R >> r.

Введя прямое и обратное сопротивление диода, его схему замещения можно представить, комбинируя резисторы и идеальные вентили.

Н апример:

Схема наглядно отражает тот факт, что сопротивление диода с изменением полярности напряжения существенно изменяется.

Так как R >> r , можно предложить более простой вариант схемы замещения:

Так как при введении данных схем замещения применяют аппроксимацию ВАХ отрезками прямых, эти схемы называют кусочно-линейными.