
Лекция 9
Урок 1. Четырехполюсники. Функции передачи
Основные понятия и определения
Часть электрической цепи, рассматриваемая по отношению к четырем её выводам (полюсам), называют четырехполюсником.
Понятие «четырехполюсник» применяют, когда интересуются только значениями максимум четырех сил токов ветвей и еще напряжениями между четырьмя узлами цепи.
В радиоэлектронике необходимо, в основном, изучать режим четырехполюсников с двумя выделенными парами выводов, называемыми портами или входами четырехполюсника. При этом полагают, что к одному из входов подключен источник сигнала, а к другому порту или выходу четырехполюсника подключена нагрузка.
Двухпортовый четырехполюсник, к одному порту которого подключен источник сигнала, а к другому нагрузка – называют проходным четырехполюсником.
Будем далее рассматривать проходные четырехполюсники.
Общее обозначение такого четырехполюсника:

На этом обозначении:
– выводы 1 и 1/ образуют входной порт или вход четырехполюсника;
– выводы 2 и 2/ образуют выходной порт или выход четырехполюсника;
– стрелкой указано направление передачи сигнала от источника, подключенного к порту 1 – 1/, к нагрузке, которая присоединяется к порту 2 – 2/.
Комплексная
амплитуда напряжения входного сигнала
обозначена как
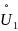 ,
а сила тока – как
,
а сила тока – как
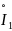 .
Соответственно, для выходного сигнала
аналогичные параметры обозначены как
.
Соответственно, для выходного сигнала
аналогичные параметры обозначены как
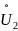 и
и
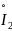 .
.
Электрический режим четырехполюсников относительно выделенных двух полюсов описывают, вводя функции цепи.
Функциями цепи называют частотные зависимости отношений комплексных амплитуд сигналов на её входе и выходе.
Среди функций цепи будем рассматривать в первую очередь функции передачи.
Функции передачи цепи
Функции передачи цепи есть частотные зависимости отношений комплексных амплитуд одноименных процессов на входе и выходе цепи.
Общее обозначение функции передачи – латинская буква Н («аш»).
Выделяют следующие функции:
функция передачи напряжения:
 функция
передачи тока:
функция
передачи тока:
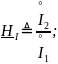 функция
передачи мощности:
функция
передачи мощности:
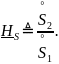
Знаками подчеркивания отмечено, что в общем случае введенные функции передачи есть комплекснозначные функции частоты. Их, как и всякие комплексные числа, можно представить в экспоненциальной записи
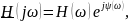
в которой
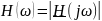 – амплитудно-частотная характеристика
(АЧХ);
– амплитудно-частотная характеристика
(АЧХ);
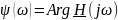 – фазо-частотная характеристика (ФЧХ).
– фазо-частотная характеристика (ФЧХ).
При
этом модуль комплексной функции передачи
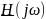 , т.е. АЧХ, есть зависимость от частоты
отношения действительных амплитуд
одноименных процессов на входе и выходе
цепи. Соответственно, аргумент комплексной
функции передачи
, т.е. АЧХ, есть зависимость от частоты
отношения действительных амплитуд
одноименных процессов на входе и выходе
цепи. Соответственно, аргумент комплексной
функции передачи
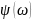 ,
т.е. ФЧХ, это упорядоченная разность фаз
одноименных процессов на выходе и входе
цепи.
,
т.е. ФЧХ, это упорядоченная разность фаз
одноименных процессов на выходе и входе
цепи.
Если ввести обобщенное обозначение для некоторого процесса в цепи (напряжения, силы тока или мощности) как a(t) с комплексной амплитудой
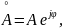
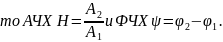
Отдельные значения функции передачи для выбранного значения частоты называют коэффициентами передачи.
В
случае, когда сравниваются комплексные
экспоненциальные колебания, функцию
передачи называют операторной
и обозначают как
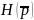 .
.
Свойства и формы представления операторной функции передачи
Операторные функции передачи линейных четырехполюсников есть дробно-рациональные функции комплексной частоты с действительными коэффициентами.
При этом общая запись операторной функции передачи всякой линейной цепи такова:
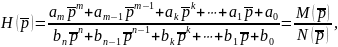
Здесь
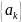 и
и
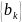 – множества действительных чисел.
Степень полинома числителя m
не превышает степени полинома знаменателя
n. Все коэффициенты
знаменателя – положительные числа.
– множества действительных чисел.
Степень полинома числителя m
не превышает степени полинома знаменателя
n. Все коэффициенты
знаменателя – положительные числа.
Согласно основной теории алгебры можно выразить функции передачи через корни числителя и знаменателя. Тогда
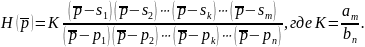
Корни
числителя из множества
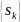 называют нулями функции
передачи. Корни знаменателя из множества
называют нулями функции
передачи. Корни знаменателя из множества
 суть полюсы передаточной
функции.
суть полюсы передаточной
функции.
Особые точки функции передачи – нули и полюсы обладают следующими свойствами:
Множества нулей и полюсов не пересекаются, т.е. не имеют общих элементов;
Нули и полюсы есть либо действительные числа, либо комплексные, составляющие комплексно-сопряженные пары.
Аналитические выражения функции передачи сложных радиоэлектронных цепей очень сложны, громоздки и трудно обозримы. В то же время множество нулей и полюсов этих функций оказываются сравнительно небольшими. Поэтому удобно описывать свойства цепей, представляя графически эти множества на плоскости комплексных чисел.
Графическое отображение особых точек функции передачи на плоскости комплексных частот называют картой или диаграммой нулей и полюсов.
Частотная избирательность цепей. Электрические фильтры
Любая реальная электрическая цепь обладает частотной избирательностью. Это означает, что при изменении частоты гармонических колебаний значения АЧХ и ФЧХ обязательно изменяются. Это свойство, как всякое другое, может быть и полезным, и вредным.
Польза частотной избирательности в том, что благодаря этому явлению можно выделять, подчеркивать, передавать с наивысшими значениями коэффициента передачи нужные гармонические колебания заданных частот и, наоборот, подавлять, передавать с малым коэффициентом передачи колебания с другими частотами. Например, можно отделять речевые электрические сигналы от токов грозовых разрядов или от «фона» гармонических колебаний электрической цепи.
Четырехполюсные цепи, пропускающие на выход с высоким коэффициентом передачи заданное множество колебаний известных частот, коэффициент передачи которых для колебания остальных частот достаточно мал, называют электрическими фильтрами.
Диапазон частот, на котором коэффициент передачи фильтра достаточно велик, называют полосой пропускания (прозрачности).
Диапазон частот, на котором коэффициент передачи фильтра достаточно мал, называют полосой задерживания (ослабления).
Частоты, являющиеся границами полосы пропускания, называют частотами среза.
Первый электрический фильтр для одновременной передачи по одной паре проводов телеграфных сигналов и сигнала речи создал российский военный связист инженер-капитан Г.Г. Игнатьев в 1880 г.
Классификация фильтров
В зависимости от полосы пропускания фильтры делят на:
Фильтры низких частот (ФНЧ). Их полоса пропускания есть область низких частот, начиная с частоты
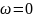 .
.


Фильтры высоких частот (ФВЧ). У них полоса пропускания – область высоких частот.
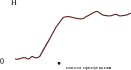
Полосно-пропускающие фильтры (ППФ) или полосовые фильтры (ПФ)
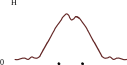
Полосно-задерживающие фильтры (ПЗФ) или режекторные фильтры (РФ)
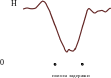
По типам применяемых элементов будем делить фильтры на:
резистивно-ёмкостные фильтры или фильтры типа RC;
реактивные фильтры или фильтры LC;
активные фильтры.
По схемотехническому исполнению фильтры делят на цепочечные и мостовые.
Сложность фильтров оценивают так же, как и для других цепей.
В частности, фильтры с n реактивными элементами, имеющими независимые электрические режимы, называют фильтрами n-го порядка.
Начнем изучение фильтров с наиболее простых примеров цепей первого порядка.
Урок 2. Резистивно-ёмкостные фильтры
Резистивно-емкостные цепи первого порядка. ФНЧ и ФВЧ
Изобразим схему замещения простейшего резистивно-ёмкостного фильтра низких частот.

К порту 1 – 1/ подключен источник с напряжением . Порт 2 – 2/ служит для подключения нагрузки фильтра.
Наилучшие частотные характеристики фильтра достигаются при подключении к нему идеального источника напряжения, и в режиме холостого хода по выходу 2 – 2/!
Найдем функцию передачи фильтра для этих условий, предлагая, что источник вырабатывает гармонические колебания с неизменной амплитудой.
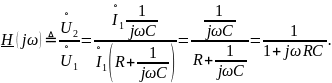
Тогда АЧХ
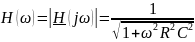
и ФЧХ
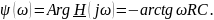
Построим графики частотных характеристик цепи.

Найдем
частоту среза фильтра. Ввиду того, что
зависимость
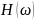 является плавной функцией, для указания
этой частоты договоримся считать верхней
границей полосы пропускания то значение
частоты, при котором относительный
уровень АЧХ
равен
является плавной функцией, для указания
этой частоты договоримся считать верхней
границей полосы пропускания то значение
частоты, при котором относительный
уровень АЧХ
равен
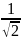 . Из этого условия получаем уравнение
. Из этого условия получаем уравнение
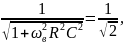
решение которого – верхняя частота среза
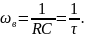
Получилось простое и удобное выражение. При таком выборе частота среза совпадает по модулю с собственной частотой рассматриваемой цепи. Она обратна постоянной времени этой цепи. С ростом сопротивления R и ёмкости C ширина полосы пропускания фильтра снижается.
Перейдем
к вычислению операторной функции
передачи. Произведя замену частот
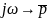 получим, что
получим, что
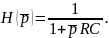
Полюс этой функции
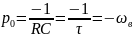
совпадает с собственной частотой цепи.
Построим карту полюсов и нулей функции на плоскости комплексной частоты .

Полюс выделен на карте крестиком. Он единственный, так как рассматривается цепь первого порядка. Он является действительным отрицательным числом.
Частотные характеристики радиоэлектронных цепей, как правило, определяют в очень широких диапазонах частот, т.е. на несколько порядков. При этом значения АЧХ также находятся в широком диапазоне. Для того, чтобы иметь возможность рассматривать частотные характеристики в больших диапазонах частот и уровней с достаточной точностью, переходят к построению графиков АЧХ и ФЧХ в логарифмическом масштабе по оси частот.
Определим логарифмическую амплитудно-частотную характеристику (ЛАЧХ) цепи соотношением
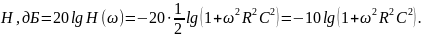
Значения этой характеристики – уровни выходного сигнала – определяют в децибелах (дБ).
Как нетрудно заметить, ЛАЧХ удобна тем, что её график проще, чем изображение «обычной» АЧХ. Действительно, в глубине полосы пропускания, когда произведение
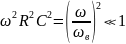
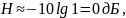
а в полосе
задерживания, если
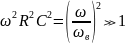
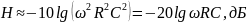
В полном логарифмическом масштабе график этой функции есть наклонная прямая. Учитывая эти приближенные результаты, аппроксимируем график ЛАЧХ двумя лучами.
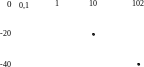
Как
видно из построений, точная ЛАЧХ,
выделенная штриховой линией, отличается
от аппроксимированных прямых только в
небольшой окрестности частоты среза,
когда
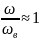 .
.
Так как ЛАЧХ в полосе задерживания с высокой точностью представляется прямой, можно просто оценивать качество фильтра, т.е. его частотную избирательность, крутизной этой прямой, называемой крутизной среза Sср.
Крутизну среза определяют в децибелах на декаду, т.е. при изменении частоты на один порядок, в десять раз, или в децибелах на октаву, т.е. при изменении частоты вдвое.
Для
рассматриваемого фильтра крутизна
среза составляет
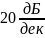 или
или
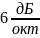 .
Это означает, что при изменении частоты
в 10 раз уровень АЧХ меняется тоже в 10
раз.
.
Это означает, что при изменении частоты
в 10 раз уровень АЧХ меняется тоже в 10
раз.
Еще одним важным параметром является крутизна фазо-частотной характеристики в полосе пропускания, называемая групповым временем задержки сигнала.
Найдем
время задержки сигнала
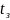 для рассматриваемого ФНЧ.
для рассматриваемого ФНЧ.
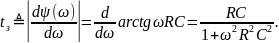
В
глубине полосы пропускания, когда
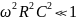 ,
т.е.
,
т.е.
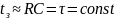 .
.
Значит, сигнал, проходящий через RC ФНЧ, задерживается в нем на время, практически равное постоянной времени.
Перейдем к изучению резистивно-емкостного фильтра высоких частот первого порядка. Он получится, если поменять местами элементы низкочастотного фильтра.

Определим комплексную функцию передачи этого фильтра.
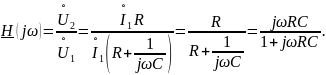
Тогда АЧХ
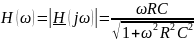
и ФЧХ
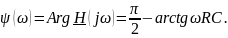
Операторная функция передачи ФВЧ
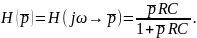
и карта полюсов и нулей

Отличие от карты ФНЧ в том, что есть нуль в начале координат. Видна закономерность – число нулей функции передачи ФВЧ совпадает с числом полюсов, т.е. с порядком цепи.
Построим графики частотных характеристик ФВЧ.

Расчеты, проведенные с привлечением полученных выражений частотных характеристик, дают следующие результаты:
– нижняя частота среза
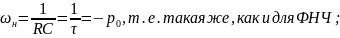
– крутизна среза в полосе задерживания
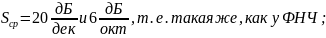
–
время задержки сигнала в полосе
пропускания
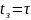 ,
т.е. равно постоянной времени цепи.
,
т.е. равно постоянной времени цепи.
Для повышения частотной избирательности рассмотренные фильтры соединяют каскадно, присоединяя к выходу предыдущего фильтра первого порядка вход последующего фильтра.
Если нагрузить ФНЧ на ФВЧ, либо включить их в обратном порядке, получится полосно-пропускающий RC фильтр. Кроме того, как полосовой фильтр применяют последовательно-параллельную RC цепь, построенную по схеме Вина.

Частотные характеристики всех перечисленных структур полосовых фильтров одинаковы.
