Лекция 12

Урок 1. Соединения четырехполюсников. Матрица соединений

При расчете режима сложных цепей применяют разбиение их схем на схемы более простых четырехполюсников с известными или с просто определяемыми параметрами. При этом параметры исходной, более сложной цепи можно найти по параметрам входящих в нее четырехполюсников, применяя простые правила.

Пусть, например, цепь разбита на два четырехполюсника так, что один из них является нагрузкой другого.

Такое соединение называют цепочечным или каскадным (соединением в каскад). При этом входящие в него четырехполюсники называются его ступенями.

Если известна матрица параметров передачи четырехполюсников и , то матрица соединения

т.е. матрица передачи каскадного соединения четырехполюсников есть произведение одноименных матриц его ступеней.

Заметим, что порядок сомножителей в расчетной формуле должен соответствовать порядку ступеней в соединении. Если, к примеру, ступени с матрицами параметров и меняются местами, т. е. ступень с матрицей становится нагрузкой ступени с матрицей , то матрица соединения описывается произведением

Это отражает тот факт, что сравниваемые соединения есть, вообще говоря, разные цепи.

Представим теперь такой вариант соединения двух двухполюсников, при котором полюсы высокого потенциала одного из них (верхние по схеме) соединяются с полюсами низкого потенциала (нижние по схеме).

Сравним комплексные амплитуды процессов на выходах четырехполюсников – исходных и получившегося. Из схемы соединения следует, что

Соединения с такими свойствами называют последовательными.

Для последовательных соединений наиболее удобны матрицы Z-параметров.

При этом матрица соединения

Значит, при последовательном соединении четырехполюсников их матрицы сопротивлений складывают.

Расмотрим ещё один вариант соединения двух четырехполюсников, когда на каждом входе объединяют полюсы высокого потенциала.

Будем считать, что для соединения четырехполюсников известны матрицы проводимостей. Обозначим их как и .

Изобразим схему соединения.

Для этого соединения

Значит, это соединение – параллельное. Для параллельного соединения

Система параметров, функция передачи и входное сопротивление X-образного реактивного моста

Для иллюстрации применения общей теории четырехполюсников рассмотрим электрический режим симметричной реактивной мостовой цепи.

Мостовыми цепями или электрическими мостами называют цепи, в которых имеется более чем один путь передачи сигнала со входа на выход.

Приведем схему X-образного симметричного реактивного моста, нагруженного на резистор с проводимостью .

Из X-образного варианта схемы видно, что входной ток попадает в нагрузку двумя путями – или через двухполюсники , или через перекрещенные двухполюсники . Симметрия этого моста в том, что его противоположные плечи имеют одинаковые параметры.

Найдем систему Y-параметров моста. Найдем сначала параметры и . Для этого замкнем нагрузку G_н проводником между узлами 2 и 2^/. Тогда мост превратится в последовательное соединение двух одинаковых цепей, каждая из которых есть кисть из элементов с проводимостями и . Тогда общая проводимость соединения, т.е. параметр

При поиске значения параметра учтем, что сила выходного тока есть разность сил токов, протекающих по элементам с проводимостью и элементам с проводимостью , т.е.

При этом есть одинаковые напряжения на последовательно соединенных одинаковых парах двухполюсников.

Значит параметр

Из-за симметрии моста . Так как мост – обратимая цепь, тогда . Поэтому матрица Y- параметров

Применим найденные Y-параметры для вычисления функции передачи напряжения. Тогда

Учтем теперь, что по условию задачи плечи моста – реактивные цепи. Пусть, для определённости, 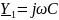, а .

Кроме того, примем проводимость нагрузки

т.е. будем считать её равной характеристической проводимости моста.

Тогда

Найдем АЧХ и ФЧХ реактивного моста:

Значит, изменяя частоту , т.е. параметры L и C, можно изменять ФЧХ. АЧХ при этом остается неизменной.

Цепи, у которых АЧХ и ФЧХ независимы друг от друга, называют неминимально-фазовыми. Мостовые цепи являются примерами таких цепей.

Найдем ещё входную проводимость симметричного моста, нагруженного на резистор с характеристической проводимостью .

Значит, входная проводимость нагруженного моста не отличается от проводимости его нагрузки. Поэтому подключение этого моста между источником и его нагрузкой не изменяет режима источника.

Цепи, имеющие:

– постоянную и неизменную амплитудно-частотную характеристику;

– изменяемую фазо-частотную характеристику;

– входные функции, совпадающие с параметрами нагрузки

применяют как корректоры фазочастотных характеристик цепей, или короче, фазовые корректоры.

Фазовые корректоры необходимы для снижения искажений сигналов, передаваемые через линейные цепи. Чем ближе ФЧХ к идеальной прямолинейной, тем меньше искажения, тем ближе форма сигнала на выходе цепи к форме сигнала на её входе.

Урок 2. Индуктивно связанный элемент

Линейные индукторы, как правило, реализуют катушками индуктивности, представляющими собой несколько витков проводника, намотанных на диэлектрическом основании. Катушки индуктивности плохо концентрируют в себе магнитное поле. Поэтому при протекании переменного тока в одной из катушек наводятся согласно закону электромагнитной индукции напряжения на соседних элементах цепи, в том числе и соседних катушках индуктивности. Для описания этого явления в теории цепей вводят четырехполюсный элемент, называемый индуктивно связанным или элементом индуктивной связи. Еще один вариант названия – совершенный трансформатор.

Элементом индуктивной связи или индуктивно связанным элементом называют воображаемый четырехполюсник, напряжения на входах (портах) которого связаны с силами входных токов соотношениями:

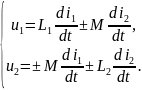
В этих соотношениях

– собственные индуктивности уединенных индуктивных элементов, описывающие явление самоиндукции;

М – взаимная индуктивность, описывающая явление взаимной магнитной индукции.

Знаки «+» и «-» при обозначении взаимной индуктивности М отражают тот факт, что напряжение взаимной индукции M может быть как синфазным (однонаправленным), так и противофазным (направленным противоположно) напряжению самоиндукции вида L .

Условное графическое обозначение вводимого элемента согласно определяющим формулам таково:

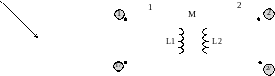
На схеме замещения приведены обозначения двух идеальных индукторов. Факт индуктивной связи отражен двухсторонней стрелкой, над которой указана взаимная индуктивность М. Кроме того, на схеме проставляют жирные точки (или звездочки), выделяющие пару так называемых одноименных выводов (полюсов) или однополярных выводов. Эти выводы соответствуют тем узлам катушек индуктивности, отображаемым данным идеальным элементом, при протекании через которые одинаково направленных токов (обоих втекающих или обоих вытекающих из узлов) напряжения взаимной индукции и самоиндукции имеют один и тот же знак, т.е. складываются арифметически. Применяя модель «элемент индуктивной связи» сопротивлением потерь и емкостями катушек пренебрегают.

При наличии на схемах индуктивно связанных элементов маркировки одноименных выводов для определения знака напряжения взаимной индукции применяют следующее правило:

Если направления отсчета сил токов элемента согласованы с направлениями отсчета напряжений на его входах, а также одинаково направлены относительно одноименных выводов, напряжение взаимной индукции имеет тот же знак, что и напряжение самоиндукции.

Значит, при описании представленной схемы замещения в уравнениях нужно ставить одни только «плюсы». Токи элемента, направленные так, что соответствующие им напряжения взаимной индукции и самоиндукции имеют один и тот же знак (т.е. направления) называют согласными, в противном случае – это встречные токи.

Представим некоторые простейшие варианты встречного протекания токов.

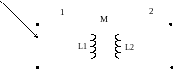
(Обратить внимание на стрелку напряжения!)

Перейдем к описанию гармонического режима элемента. Применяя к исходным уравнениям метод комплексных амплитуд, получаем:

В этих уравнениях

– взаимное индуктивное сопротивление или сопротивление индуктивной связи из-за явления взаимной магнитной индукции.

Перейдем к матричной записи уравнений.

При этом матрица коэффициентов

есть матрица параметров рассматриваемого четырехполюсника.

Воспользуемся элементами данной матрицы четырехполюсника для нахождения функций этой цепи.

Сначала найдем входное сопротивление элемента со стороны первого порта (выводов 1-1^/) при условии, что он нагружен на двухполюсник с комплексным сопротивлением .

Известно, что

Из-за обратимости элемента . Кроме того, и .

Поэтому

Как видно, входное сопротивление нагруженного элемента отличается от сопротивления входного индуктора на величину сопротивления, внесенного нагрузкой. Оно больше по модулю сопротивления элемента . В отсутствие индуктивной связи, когда М = 0, либо в режиме холостого хода по порту 2, когда входное сопротивление элемента индуктивной связи совпадает с сопротивлением индуктора , подключенного к порту 1.

Рассмотрим особенности входного сопротивления элемента для важного случая сильной нагрузки, когда . Тогда дробь

отчего

В частности, в режиме короткого замыкания по порту 2, когда

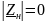
где эквивалентная индуктивность

Значит, в режиме короткого замыкания по выходу (порту 2) индуктивно связанный элемент представляет собой идеальный индуктор, сопротивление и индуктивность которого меньше, чем у «входного» элемента, подключенного к порту 1.

Индуктивность линейных индукторов не может быть отрицательной. Исходя из этого, получаем важное неравенство:

из которого получаем ограничение на взаимную индуктивность

Введем параметр, называемый коэффициентом связи,

По определению и взаимная индуктивность

Введя коэффициент связи, получаем, что и

Отношение обозначим как , где

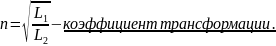
Тогда

В случае сильной нагрузки и сильной связи, когда

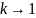
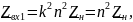
т.е. входное сопротивление элемента пропорционально сопротивлению нагрузки.

Если , то , т.е. нагруженный элемент связи – тоже резистор.

Индуктивно связанный элемент, для которого в точности соблюдается равенство

называют идеальным трансформатором.

Найдем теперь функцию передачи тока.

В случае сильной нагрузки, когда

Значит, в этом случае функция передачи тока практически не зависит от частоты. Её значения определяются только коэффициентом связи k и коэффициентом трансформации n.

Для идеального трансформатора с k = 1

т.е. функция передачи тока равна по модулю коэффициенту трансформации.

Определим также функцию передачи напряжения. Индуктивно связанный элемент при сильной связи по определению не имеет потерь энергии (ни «в меди», ни через магнитное поле рассеяния).

Поэтому полные мощности процессов на его входе и выходе совпадают, т.е.

Поэтому для данного элемента

Значит, функция передачи напряжения элемента индуктивной связи при сильной нагрузке, когда и при равна

Значит, идеальный трансформатор, т.е. элемент индуктивной связи с k = 1, обладает следующими свойствами:

Его функции и не зависят от частоты и определяются значением коэффициента трансформации .

Воображаемый элемент «идеальный трансформатор» очень удобен для расчетов.