3. Інтегральна теорема Муавра – Лапласа.

Сформулюємо задачу. Необхідно обчислити ймовірність того, що подія, яка відповідає умовам схеми Бернуллі, в n незалежних випробуваннях з’явиться не менше ніж k₁ раз і не більше ніж k₂ рази, за умови, що кількість випробувань n досить велика.

Теорема 3.3. (Інтегральна теорема Муавра – Лапласа). Якщо ймовірність р появи події А в кожному незалежному випробуванні постійна і відмінна від нуля та одиниці, то ймовірність Р_n(k₁, k₂) того, що подія А з’явиться в n незалежних випробуваннях від k₁ до k₂ раз наближено дорівнює визначеному інтегралу

де ,

Функція називається функцією Лапласа. Її значення занесені в таблицю. Функція Лапласа – непарна.

Для того, щоб мати змогу скористатися функцією Лапласа перетворимо її:

Отже

Приклад:

Ймовірність влучення стрілком в мішень при одному пострілі дорівнює 0,75. Обчислити ймовірність того, що при 100 пострілах в мішень буде влучено:

• 1. Не менше 70 і не більше 80 разів

• 2. Не більше 70 разів

5. Теорема Пуассона для малоймовірних подій

Нехай проводиться n незалежних випробувань, в кожному з яких подія А може або з’явитися, або не з’явитися з однаковою ймовірністю р. Розглянемо в якості ДВВ Х – кількість появ події А в таких випробуваннях.

Якщо ймовірність появи події А у всіх випробуваннях дуже мала (p≤0,1), то ймовірності, що відповідають можливим значенням ДВВ Х обчислюється за формулою Пуассона

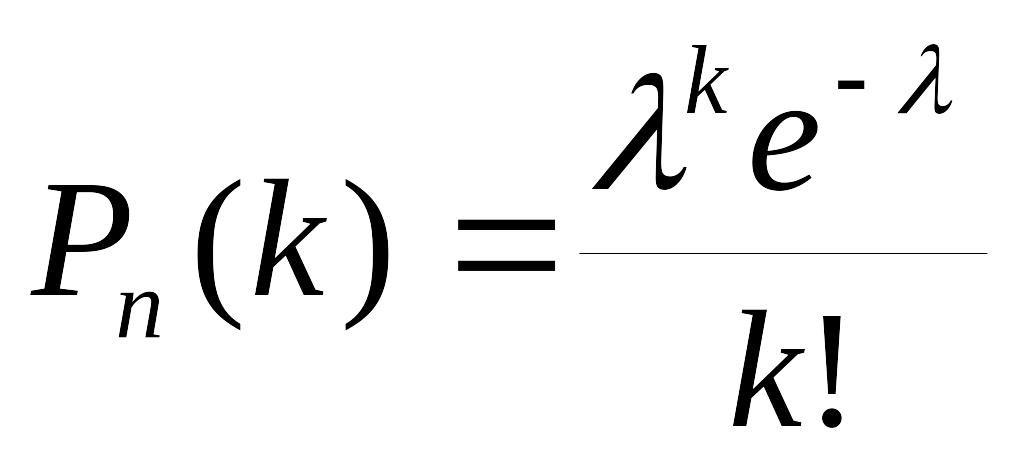, где =n·p

Питання для самоконтролю

1. Повторні незалежні випробування

2. Формула Бернуллі

3. Локальна теорема Муавра – Лапласа

4. Інтегральна теорема Муавра – Лапласа

5. Теорема Пуассона для малоймовірних подій

Тема 4. Випадкові величини та їх економічна інтерпретація

Лекція 4.

Випадкові величини

Мета: ввести означення одновимірних випадкових величин, методів їх представлення.

План лекції:

1. Означення одновимірної випадкової величини, її закон розподілу

2. Функція розподілу ймовірності випадкової величини та її властивості

3. Щільність розподілу

4. Економічна інтерпретація випадкових величин

Рекомендована література: [1] ст. 55-63, [4] ст. 61-72, [6] ст. 67-82

1. Означення одновимірної випадкової величини , її закон розподілу

Випадковою називають величину, яка в результаті випробування приймає те чи інше (але при цьому тільки одне) можливе значення, наперед невідоме, таке, що змінюється від випробування до випробування і залежить від випадкових обставин.

На відміну від випадкової події, яка є якісною характеристикою випадкового результату випробування, випадкова величина характеризує результат випробування кількісно.

Дискретною називають випадкову величину, що приймає окремі, ізольовані можливі значення з визначеними ймовірностями.

Цілочисловою називають ДВВ, можливі значення якої приймають тільки цілі значення з будь – якого обмеженого або необмеженого проміжку.

Неперервною називають випадкову величину, що може приймати будь-які значення з деякого обмеженого або необмеженого проміжку.

Випадкові величини прийнять позначати останніми великими літерами латинського алфавіту Х, Y, Z, а їх можливі значення – відповідними малими літерами.

Законом розподілу дискретної випадкової величини (ДВВ) називають будь – яке співвідношення, що встановлює зв’язок між можливими значеннями випадкової величини та відповідними їм ймовірностями.

Для ДВВ закон розподілу може бути задано:

• у вигляді таблиці

  Х
  р

• аналітично (тобто за допомогою формули)

• графічно (цей вид завдання закону розподілу використовують для наочності . На графіку відкладають можливі значення ВВ та відповідні їм ймовірності. Точки сполучає ламана, яку називають багатокутником або полігоном розподілу ).

Приклад:

Два стрілки здійснюють по одному пострілу в мішень. Ймовірність влучення в неї першим стрілком дорівнює 0,5, другим – 0,4. Скласти закон розподілу кількості влучень в мішень і побудувати полігон розподілу