УТВЕРЖДАЮ
Ректор университета
____________ А.В. Лагерев
«___»__________2011 г.
Методы математической физики
Методические указания к выполнению самостоятельной работы
для студентов очной (дневной) формы обучения
специальностей 210106 – «Промышленная электроника»,
210104 – «Микроэлектроника и твердотельная электроника»
Брянск 2011
УДК 511
Методы математической физики: методические указания к выполнению самостоятельной работы для студентов очной (дневной) формы обучения специальностей 210106 - «Промышленная электроника», 210104 – «Микроэлектроника и твердотельная электроника».- Брянск: БГТУ, 2011. – 48 с.
Разработали: Г. Г. Цуленева, доцент каф. «ВМ»
Г. Г. Вискина, ст. преп. каф. «ВМ»
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол № 5 от 25.01.2011)
Оглавление Предисловие…………………………………………….…………4
Методические указания к выполнению заданий расчётно-графической работы……………………………………………….5
Условия заданий расчетно-графической работы…………….....28
Примерный вариант контрольной работы………...…………….36
Теоретические вопросы к зачёту и экзамену…………………...37
Список рекомендуемой литературы……...……………………..40
Предисловие
В соответствии с Государственным образовательным стандартом высшего профессионального образования специальности 210106 - «Промышленная электроника», 210104 – «Микроэлектроника и твердотельная электроника» объём самостоятельной работы студентов (СРС) очной формы обучения должен составлять не менее 50% от общего объёма теоретического обучения. Таким образом, возрастает важность самостоятельной работы как вида учебной деятельности студентов.
К видам СРС по дисциплине «Методы математической физики» относятся самостоятельное изучение теоретического материала, выполнение домашнего задания, решение задач расчётно-графической работы (РГР), подготовка к контрольной работе, зачёту и экзамену.
Данные методические указания предназначены для студентов очной формы обучения специальности 210106 - «Промышленная электроника», 210104 – «Микроэлектроника и твердотельная электроника», изучающих дисциплину «Методы математической физики» в VI семестре. Они содержат условия задач РГР и указания к их решению, примеры решения задач РГР, образец варианта контрольной работы, теоретические вопросы к зачёту и экзамену, список рекомендуемой литературы.
1. Методические указания к выполнению заданий расчетно-графической работы
Расчётно-графическая работа содержит 10 задач.
В заданиях № 1 и № 2 необходимо вычислить поток и циркуляцию векторного поля.
В задании № 3 следует привести к каноническому виду линейное дифференциальное уравнение в частных производных второго порядка и найти его общее решение.
В заданиях № 4а, 4б необходимо решить краевую задачу для уравнений гиперболического типа, № 5а, 5б – параболического типа, № 6а, 6б, 6в – эллиптического типа.
Задание
№ 1. Найти
поток векторного поля
через замкнутую поверхность
(нормаль внешняя).
Указания к решению.
Пусть
в области
задано некоторое векторное поле
,
где
- непрерывно дифференцируемые в области
функции. Пусть
- гладкая ориентируемая поверхность,
на которой выбрана определённая сторона,
задаваемая единичной нормалью
к
этой поверхности.
Потоком
векторного поля
через поверхность
в направлении единичной нормали
называют поверхностный интеграл первого
рода:
. 
Поверхностный интеграл первого рода в формуле связан с поверхностным интегралом второго рода равенством
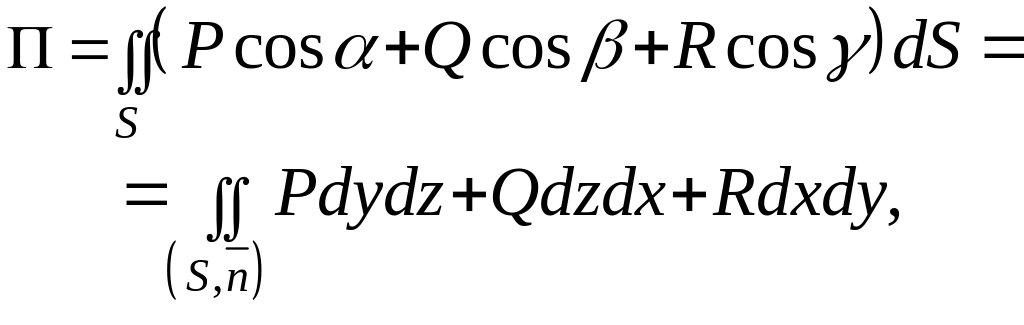
которое даёт ещё один способ вычисления потока.
Для вычисления потока векторного поля через замкнутую поверхность часто применяют формулу Гаусса-Остроградского:
,
где
- тело, ограниченное поверхностью
.
Однако следует иметь ввиду, что для применения этой формулы необходимо, чтобы векторное поле было непрерывно-дифференцируемым внутри поверхности . Это условие всегда выполнено, если область , в которой рассматривается поверхность пространственно односвязная. (Область называется пространственно односвязной, если из того, что замкнутая поверхность лежит в следует, что тело , границей которого является поверхность , тоже лежит в .
Пример
1. Вычислить
поток вектора
через замкнутую поверхность
по определению, 2) по формуле Остроградского.
Решение.
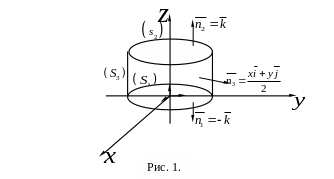
Поток вектора равен сумме
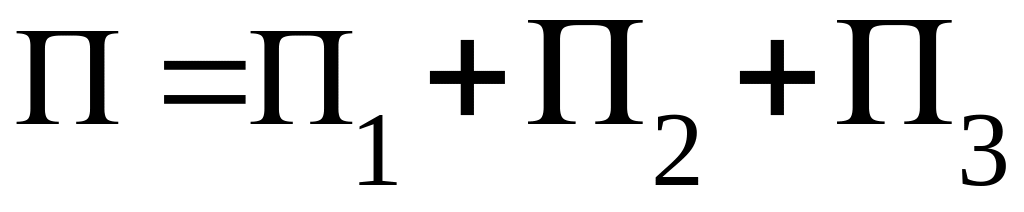(рис. 1), где
(
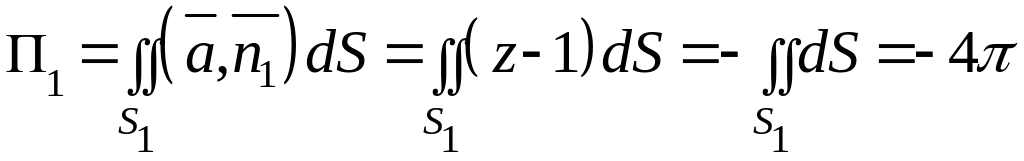
на поверхности
),
(
на поверхности
),
,
так как
.
Перейдём на цилиндре к криволинейным координатам
.
Тогда
.
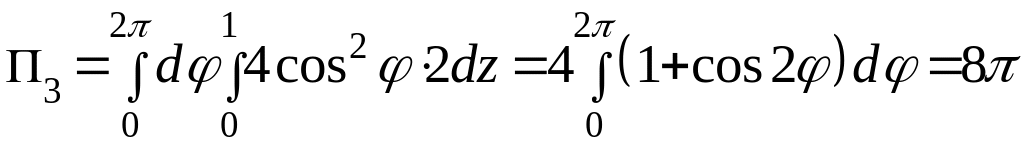Следовательно,
.
По формуле Гаусса-Остроградского имеем
.
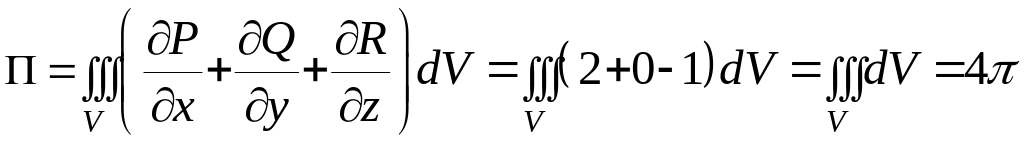Задание
№ 2. Найти
модуль циркуляции векторного поля
вдоль контура
.
Указания к решению.
Пусть - векторное поле, заданное в некоторой области , и функции - непрерывно дифференцируемые в области . Пусть - замкнутая гладкая кривая, расположенная в области . Криволинейный интеграл
называется циркуляцией векторного поля вдоль кривой .
Для вычисления циркуляции векторного поля часто применяют формулу Стокса.
Теорема
Стокса. Пусть
- гладкая ориентируемая поверхность, а
- замкнутая гладкая кривая, являющаяся
границей поверхности
.
Пусть
- единичная нормаль к поверхности
,
задающая одну из её сторон. Пусть
векторное поле
непрерывно дифференцируемо на
и на
.
Тогда
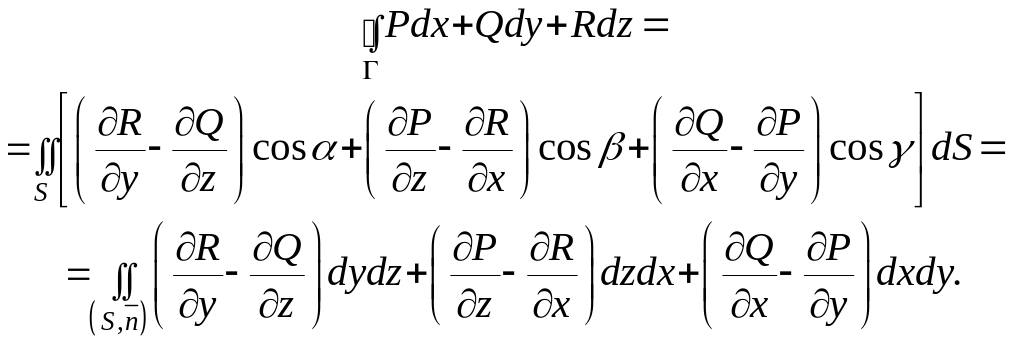
Пример
2. Вычислить
циркуляцию пространственного векторного
поля
вдоль эллипса
,
получающегося пересечением цилиндра
с плоскостью
(при взгляде с положительного направления
оси
обход контура
совершается против часовой стрелки).
Решение.
Первый способ.
Запишем
параметрические уравнения эллипса:
.
При изменении параметра
от 0 до
получаем требуемое направление обхода
контура
.
Вычислим
теперь циркуляцию:
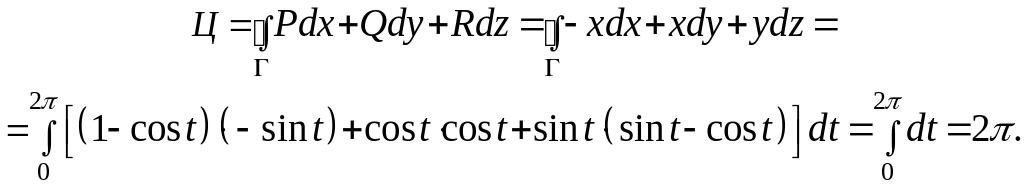
Второй способ.
Вычислим
циркуляцию, применив формулу Стокса,
причём в качестве поверхности
,
ограничиваемой кривой
,
выберем часть плоскости
,
лежащей внутри цилиндра
.
Единичную нормаль к плоскости выберем
так, чтобы, глядя с её конца, направление
обхода контура
проходило против часовой стрелки. Такой
единичной нормалью будет вектор
.
По формуле Стокса имеем:
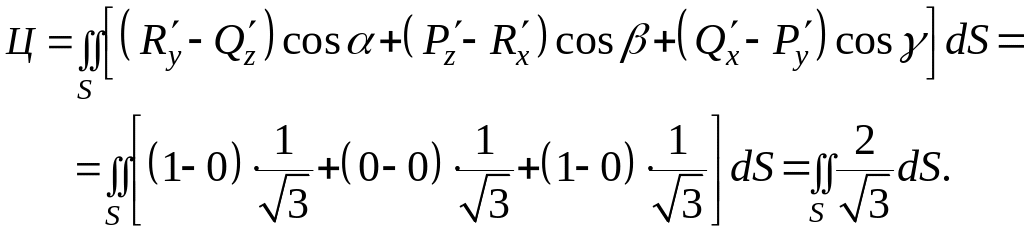
Вычисление
последнего интеграла сведём к вычислению
двойного интеграла по области
,
являющейся проекцией поверхности
на плоскость
.
Этой областью будет круг
.
Поскольку
,
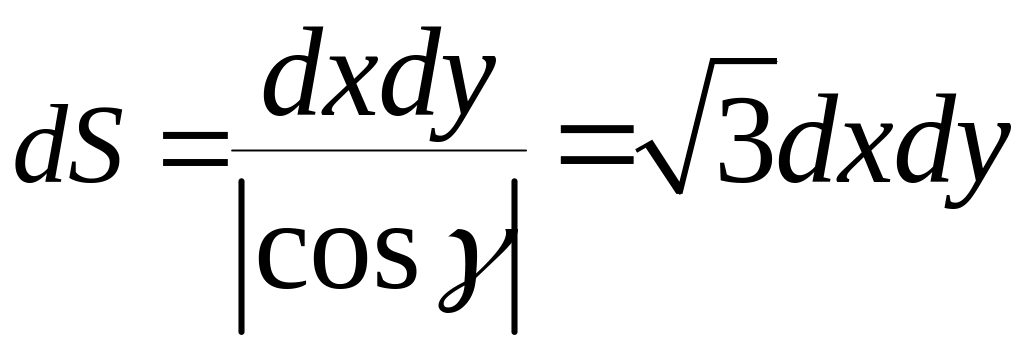то окончательно получаем:
.
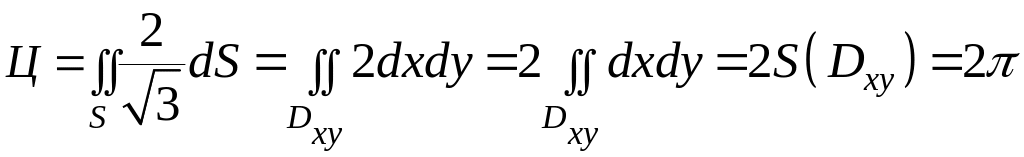Задание № 3. Определить тип уравнения
,
привести его к каноническому виду и найти его общее решение.
Указания к решению.
Определяем тип уравнения по знаку выражения
если
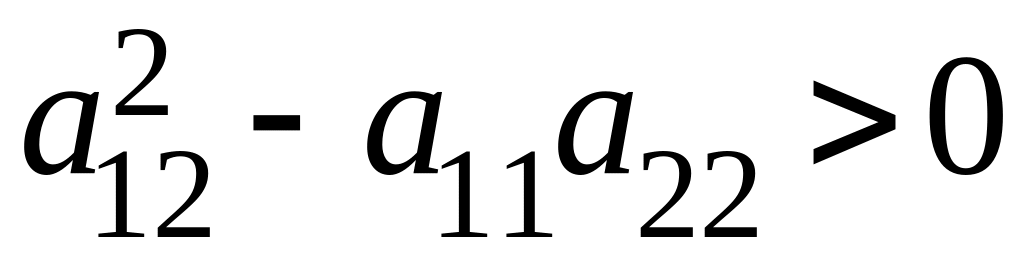в некоторой точке, то уравнение
называется уравнением гиперболического
типа в этой
точке;если
в некоторой точке, то уравнение
называется уравнением эллиптического
типа в этой
точке;если
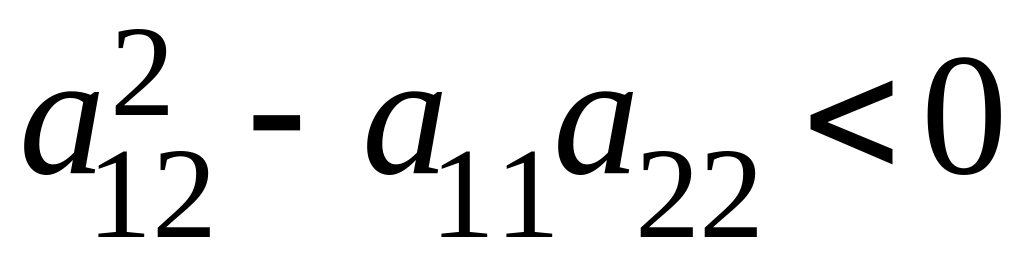в некоторой точке, то уравнение
называется уравнением параболического
типа в этой
точке.
Составляем характеристическое уравнение
и
решаем его относительно
.
Делаем замену переменных
где
в случае уравнения гиперболического типа
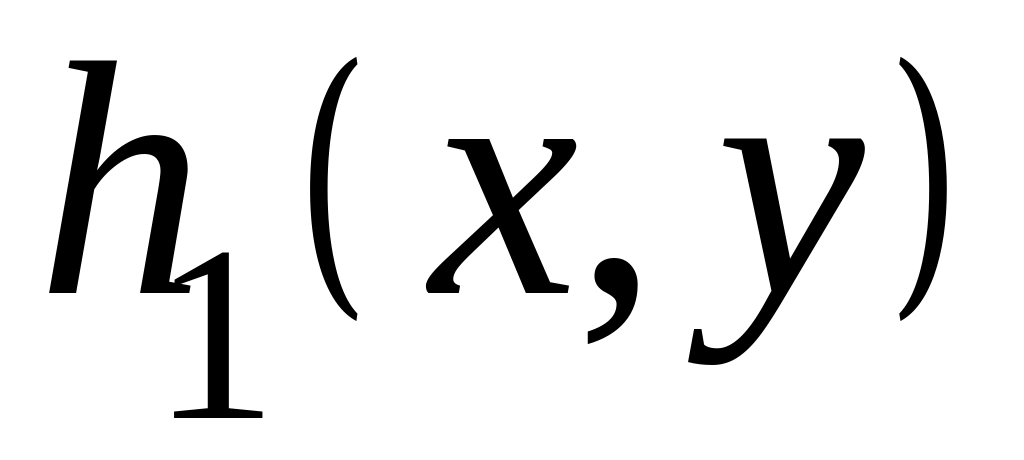и
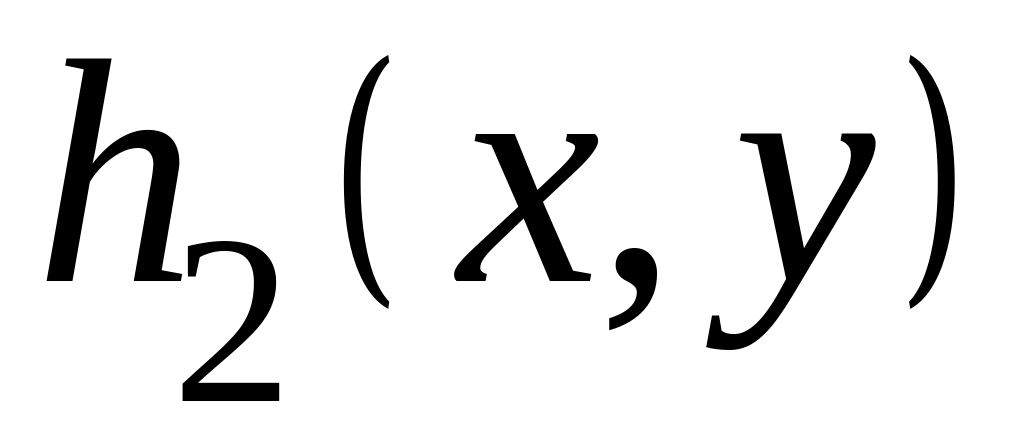- независимые общие интегралы уравнения
характеристик
;в случае уравнения параболического типа - общий интеграл уравнения характеристик и - произвольная дважды дифференцируемая функция, не выражающаяся через ;
в случае уравнения эллиптического типа и - вещественная и мнимая части любого из двух общих интегралов уравнения характеристик .
В результате замены переменных уравнение примет один из трёх канонических видов:
в случае уравнения гиперболического типа
;
в случае уравнения параболического типа
;
в случае уравнения эллиптического типа
.
Ищем общее решение полученного уравнения.
Пример 3. Определить тип уравнения
, 
привести его к каноническому виду и найти его общее решение.
Решение.
Имеем:
следовательно,
уравнение является уравнением
гиперболического типа во всей плоскости
.
Составляем характеристическое уравнение.
, 
,
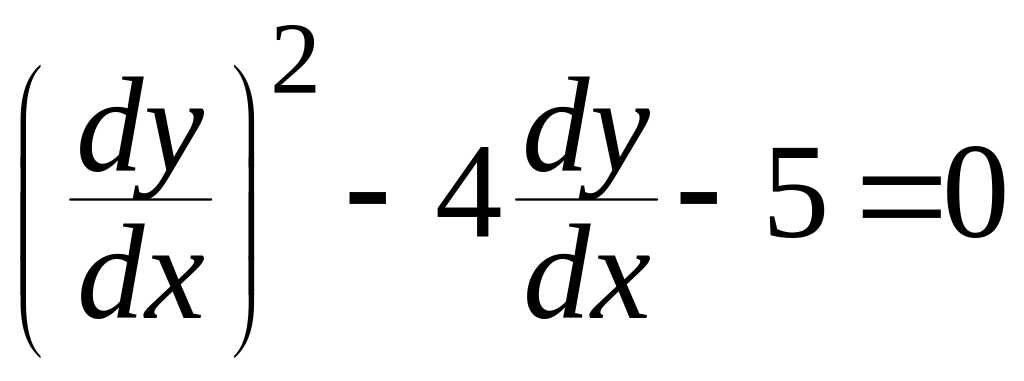и
,
и
,
и
.
Таким образом, уравнение характеристик имеет два интеграла:
и
.
Делаем замену переменной
. 
По правилу дифференцирования сложной функции
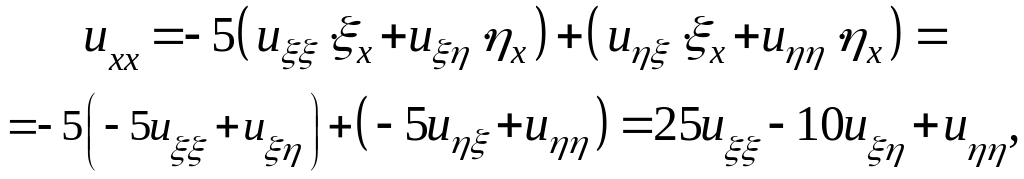
В результате замены переменных уравнение принимает вид
Таким образом,
. 
Интегрируем уравнение
по
,
получаем
. 
Интегрируя
уравнение
по
,
получаем
.
Следовательно,
общее решение уравнения
имеет вид
, 
где
и
- произвольные дважды дифференцируемые
функции.
Подставляя в
и
,
получаем общее решение уравнения
.
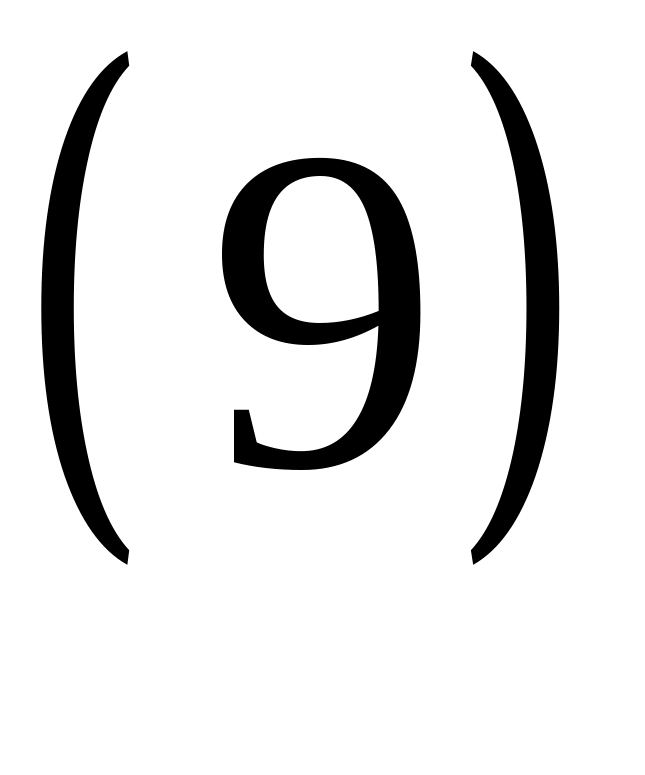
Делаем проверку и записываем ответ.
Пример 4. Найти общее решение уравнения
, 
привести его к каноническому виду и найти его общее решение.
Решение.
Имеем:
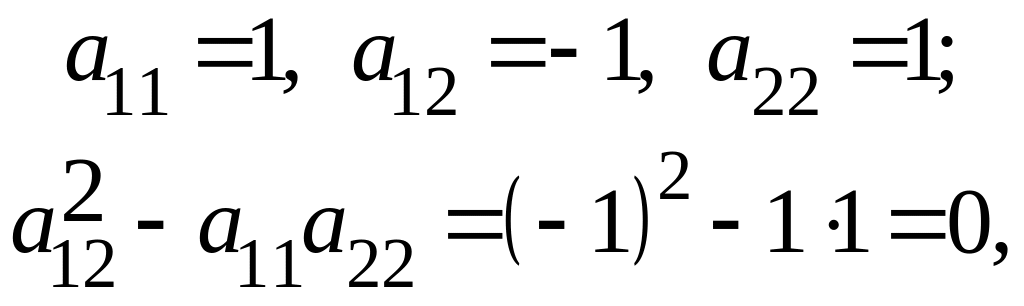
следовательно, уравнение является уравнением параболического типа во всей плоскости .
Составляем и решаем характеристическое уравнение.
, 
,
,
.
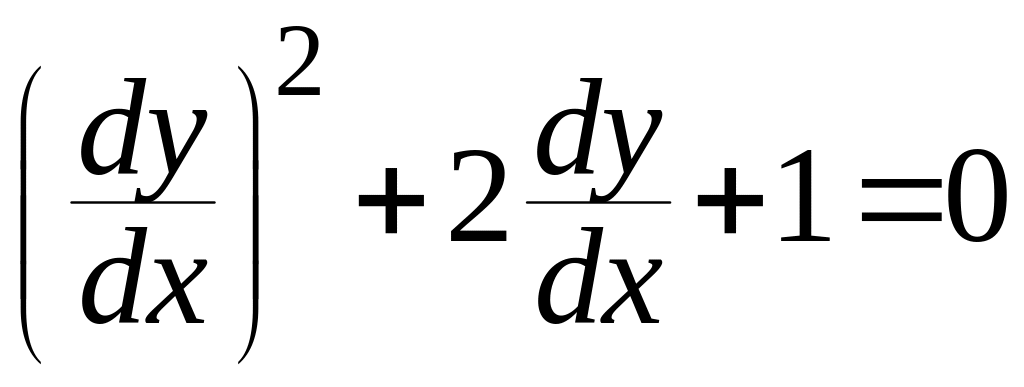Таким образом, уравнение характеристик имеет один общий интеграл
Делаем замену переменной
. 
В
качестве
можно было бы взять и любую другую дважды
дифференцируемую функцию, не выражающуюся
через
.
Приводим уравнение к каноническому виду. Получаем уравнение
. 
Чтобы найти общее решение уравнения , составляем соответствующее характеристическое уравнение
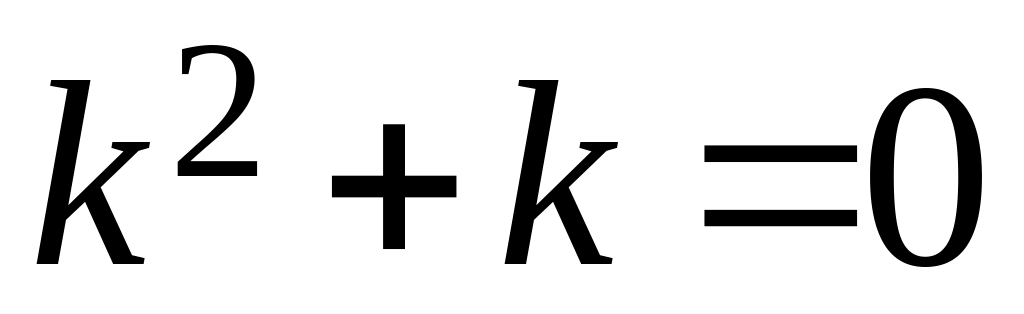и находим его корни
и
.
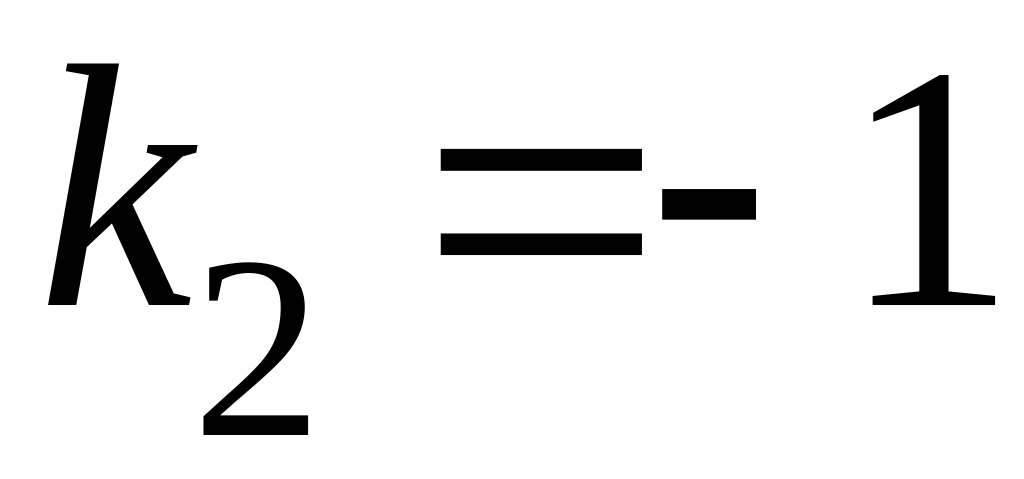Следовательно,
общее решение уравнения
можно записать в виде
, 
где
и
- произвольные дважды дифференцируемые
функции.
Подставляя в
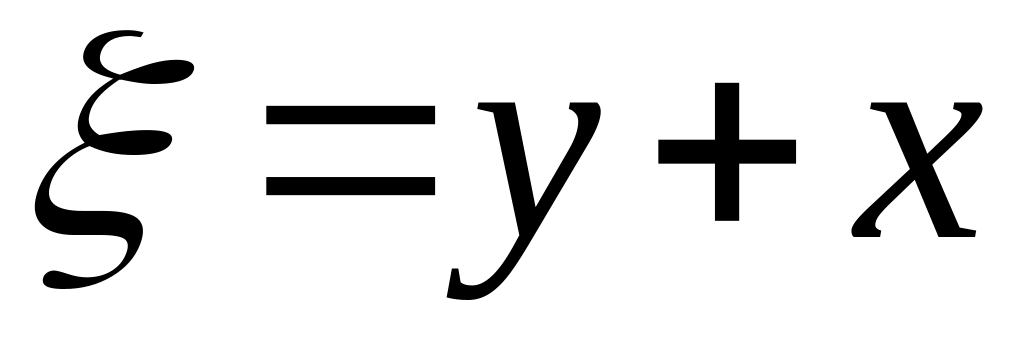и
,
получаем общее решение уравнения
.
Делаем
проверку, подставляя
в уравнение
,
и записываем ответ.
Задание № 4а. Решить смешанную задачу.
Указания к решению.
Вводим вспомогательную функцию
,
значения
которой при
и
совпадают со значениями неизвестной
функции
,
т.е.
,
.
Рассмотрим функцию
.
Очевидно,
что
.
Перейдем в уравнении и в начальных условиях к функции
:
(т.к.
и
).
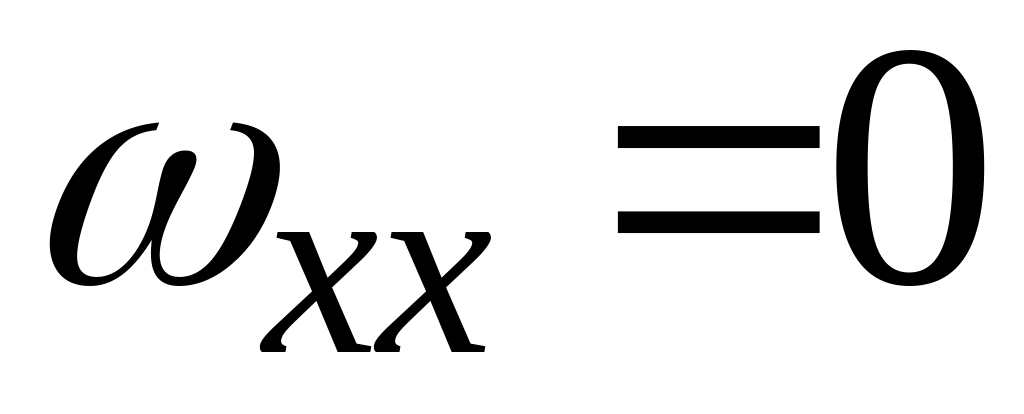Получаем уравнение
.
Для начальных условий имеем
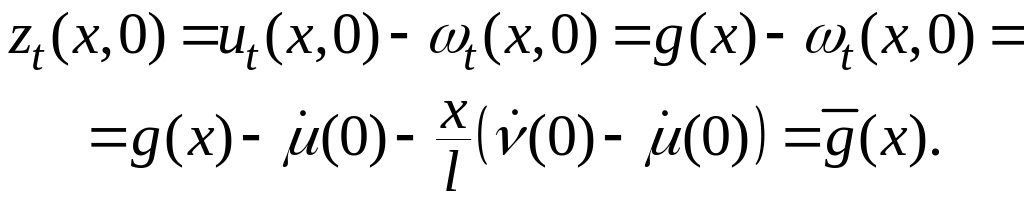
Получаем краевую задачу
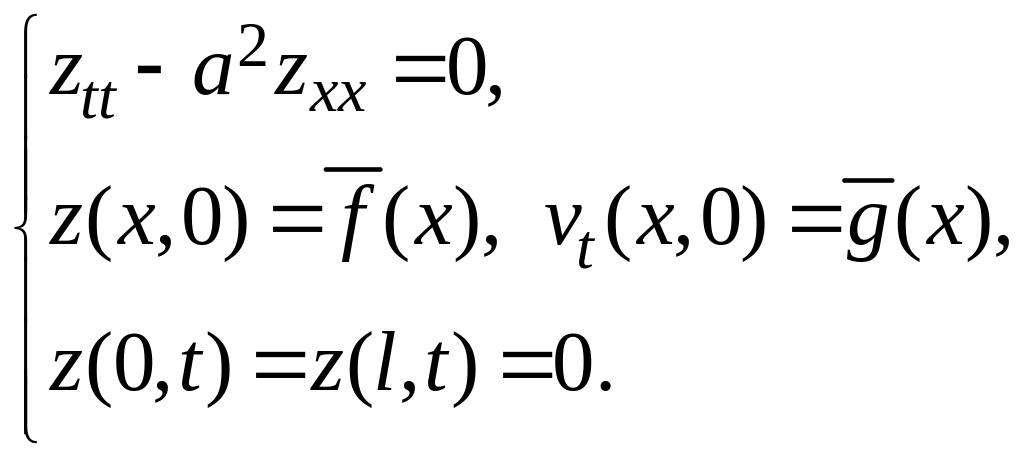
Ищем решение
уравнения
в виде
,
причём
,
т. е.
.
Для этого подставляем
в уравнение
и разделяем переменные. Получаем
.
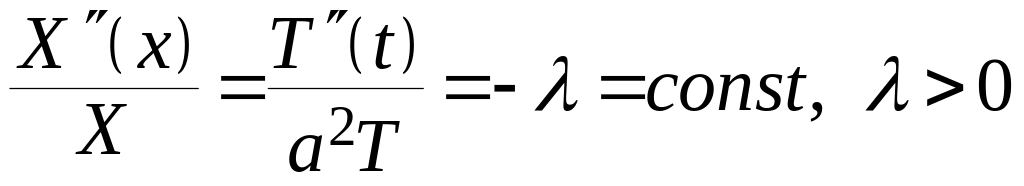Поэтому
функции
и
являются решениями связанных задач
а) 
;
б) 
.
Решаем задачу а)
Уравнение
имеет общее решение
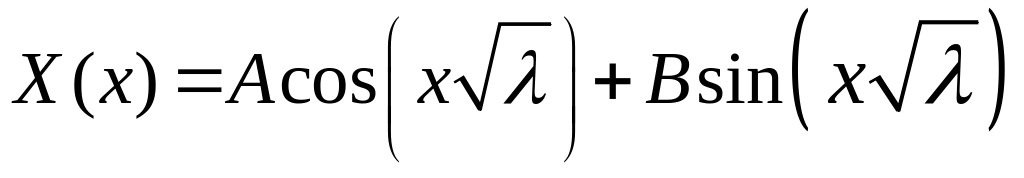
Из
граничных условий
следует, что
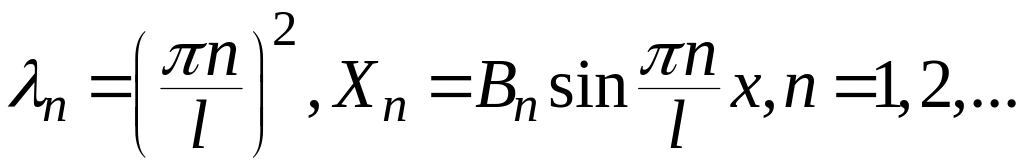
Решаем задачу б). При
имеем
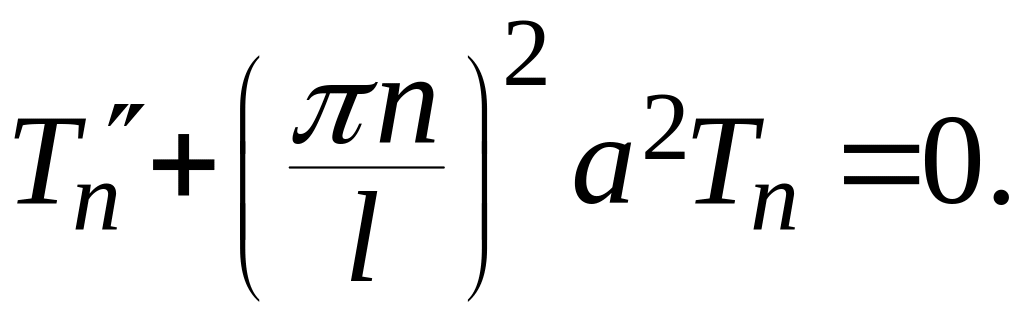
Общее решение этого уравнения
Итак, вспомогательные решения уравнения
имеют вид
где
- постоянные, которые предстоит найти.
Решение задачи
ищем в виде
Эта
функция является решением уравнения
и удовлетворяет граничным условиям
при любых
и
,
при которых ряд
сходится и его можно дважды дифференцировать
почленно.
Находим коэффициенты и
,
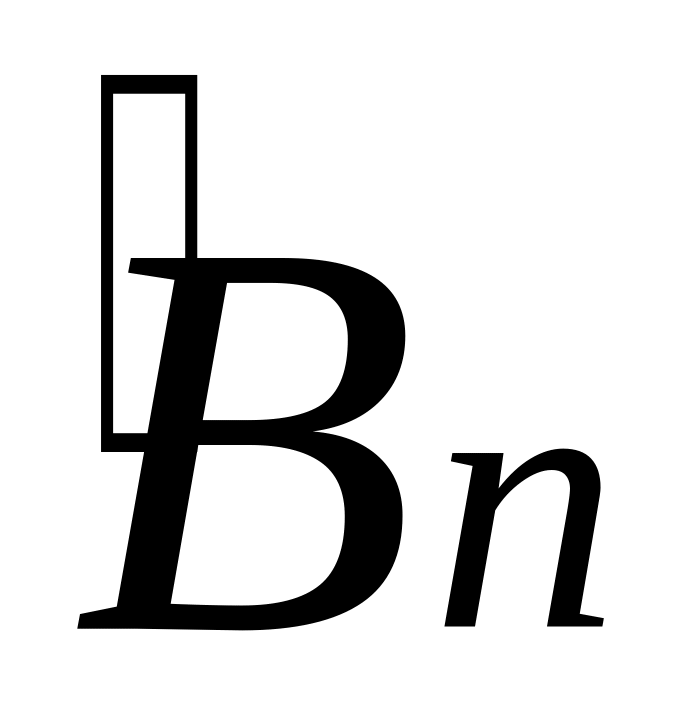при которых
удовлетворяет начальным условиям
.
Полагая
в
,
получаем
Отсюда
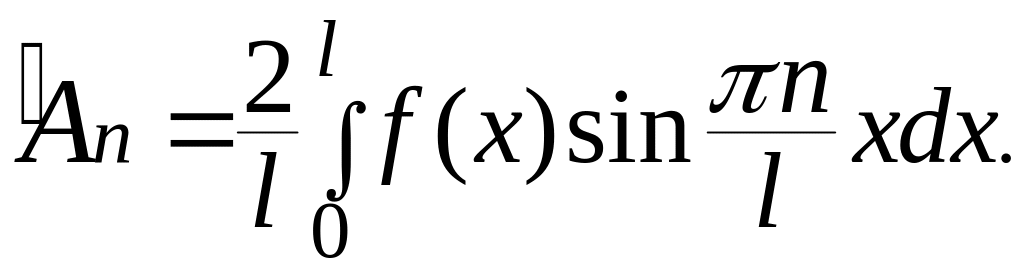
Дифференцируя равенство , имеем
Полагая
здесь
и используя начальное условие
,
получаем
Отсюда
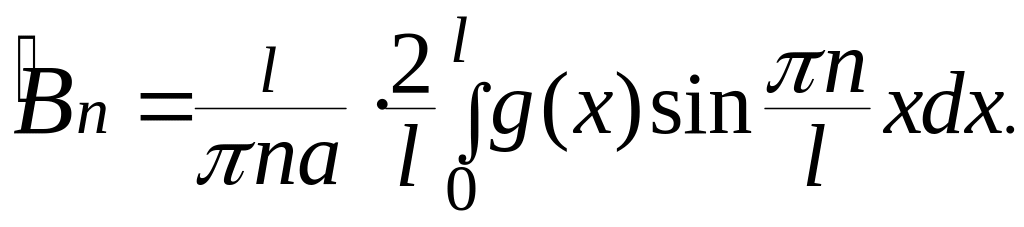
Подставляя эти коэффициенты в формулу , получаем решение задачи
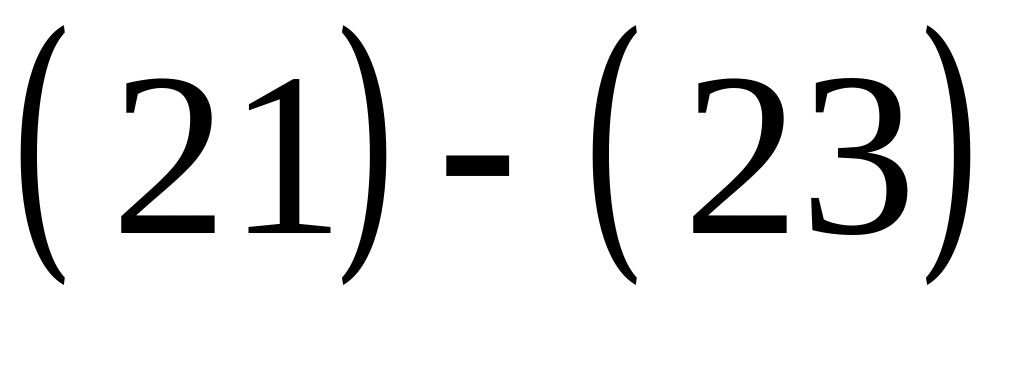.Записываем ответ в виде
.
Пример 5. Решить смешанную задачу.
Решение.
В
задаче
.
Вводим вспомогательную функцию
.
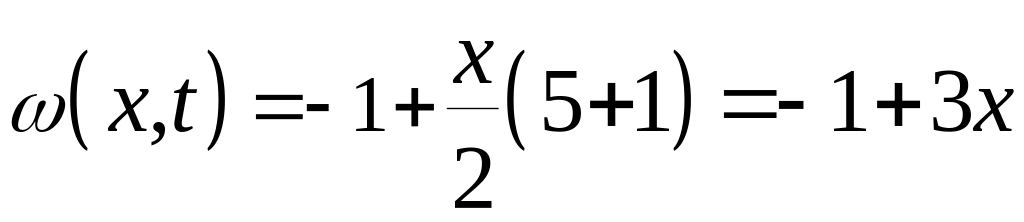Ищем решение задачи в виде
.
Сформулируем задачу для новой неизвестной функции
.
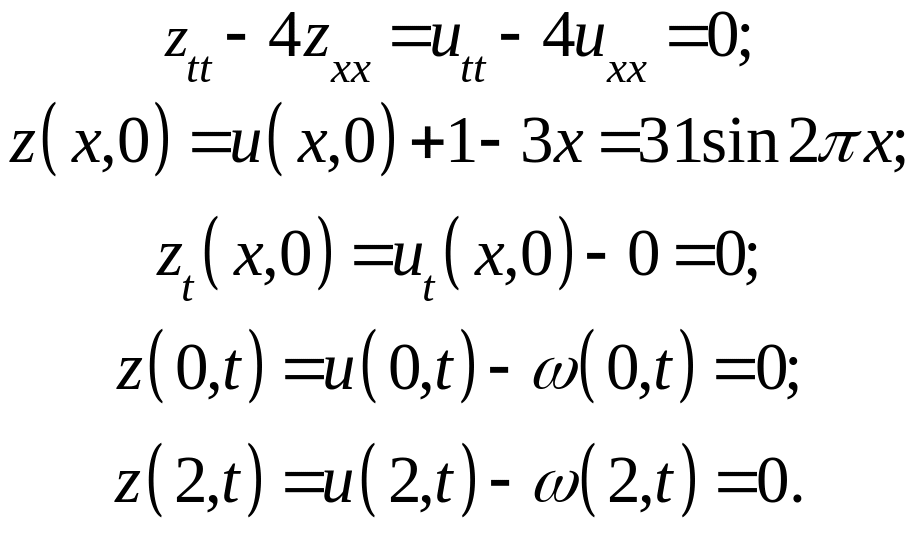
Получаем краевую задачу
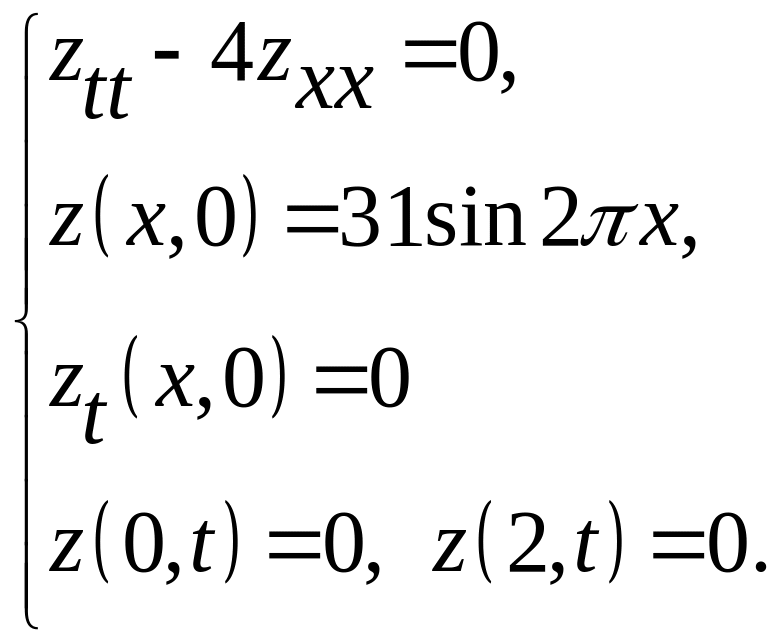
Выполняя пункты 5 – 10 указания к решению задачи, получим решение в виде ряда
.
Ищем коэффициенты
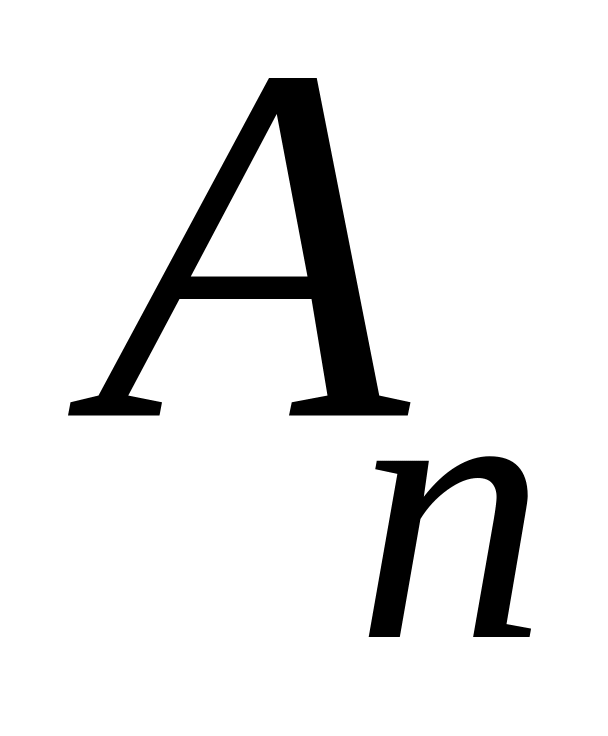и
,
используя начальные условия
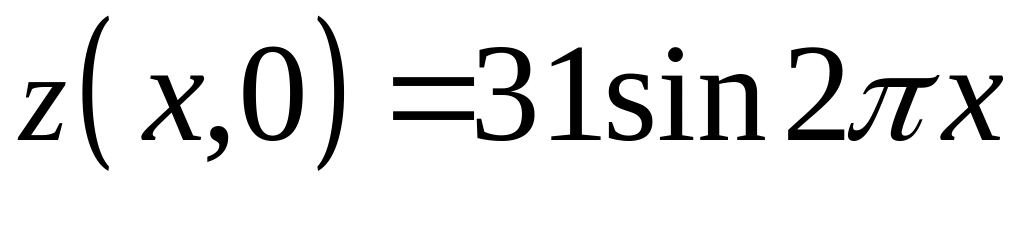и
.
.
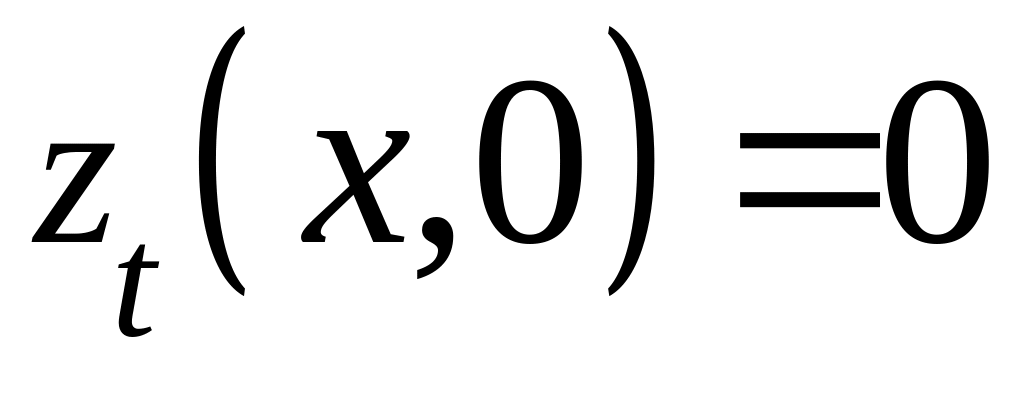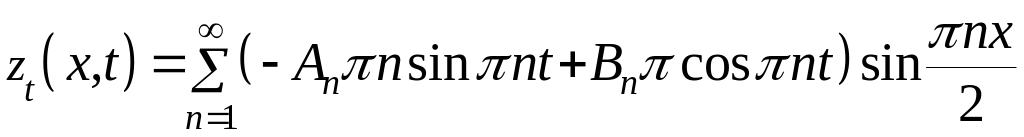При получим
,
.
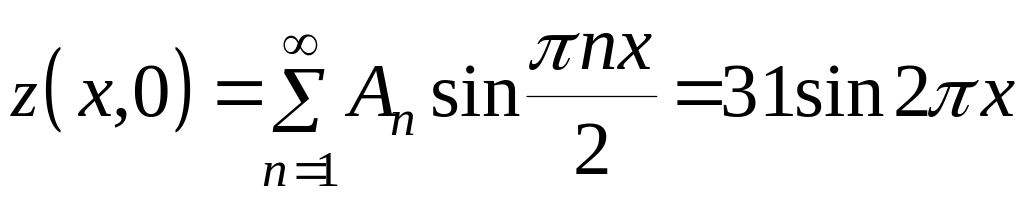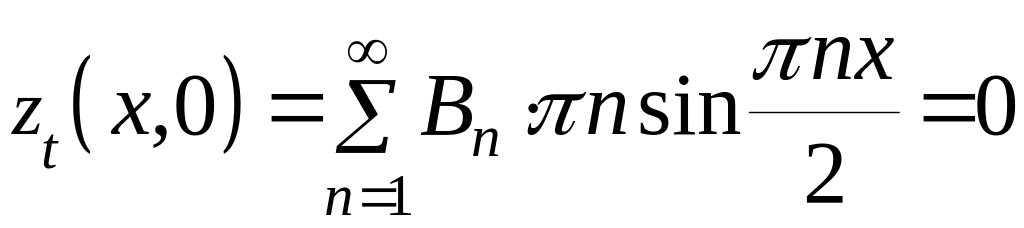Очевидно,
что при
,
при
.
для
.
Получаем функцию
.
Решение исходной задачи имеет вид
.
Ответ: .
Задание № 4б. Решить первую смешанную задачу для неоднородного волнового уравнения на отрезке:
Указания к решению
Поскольку начальные условия однородные, применим метод разложения по собственным функциям соответствующей однородной задачи.
Решение
ищем в виде ряда
. 
Здесь
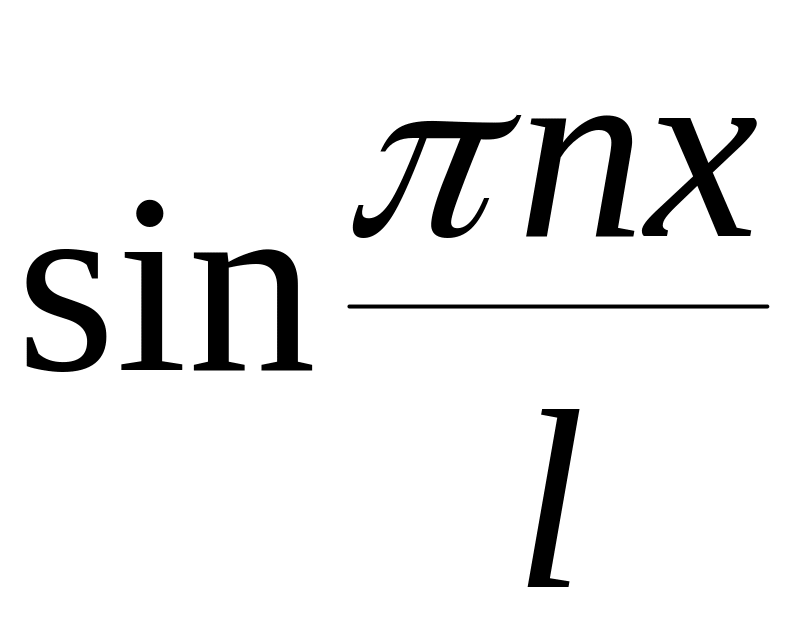- собственные функции однородной краевой
задачи, и граничные условия
выполняются автоматически.
Определим функции
так, чтобы функция
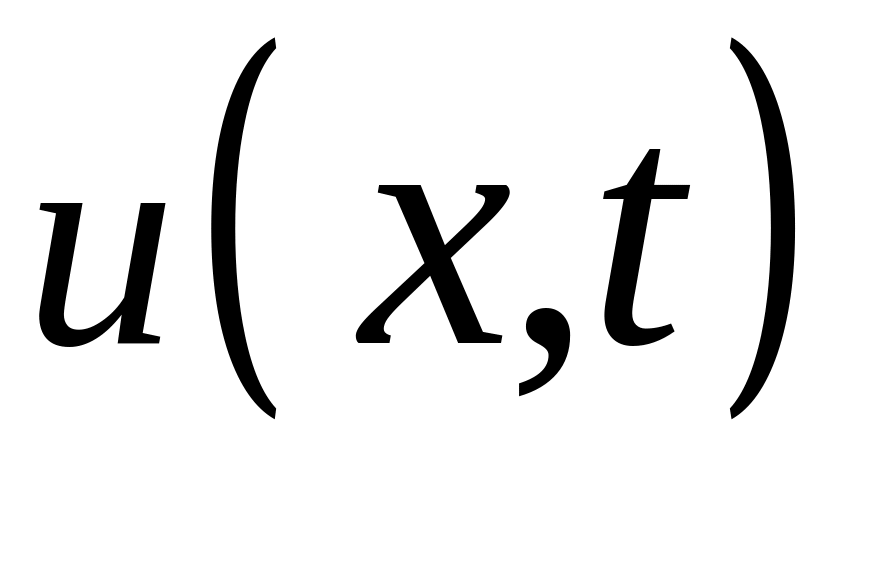удовлетворяла уравнению
и начальным условиям
.
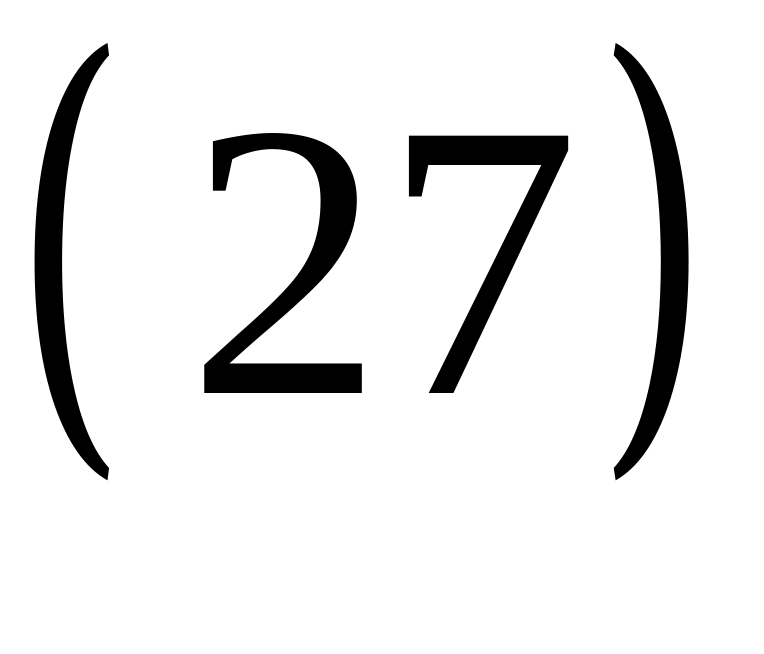Подставив в виде в уравнение , получим
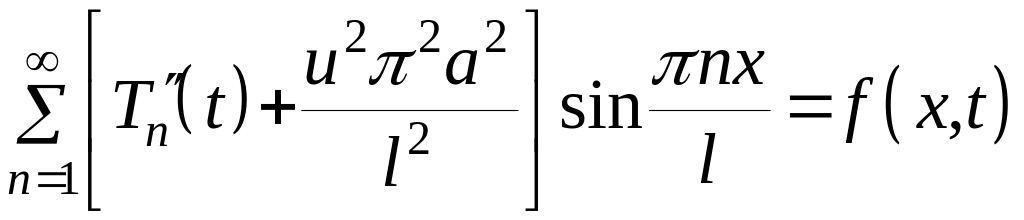
Разложим функцию
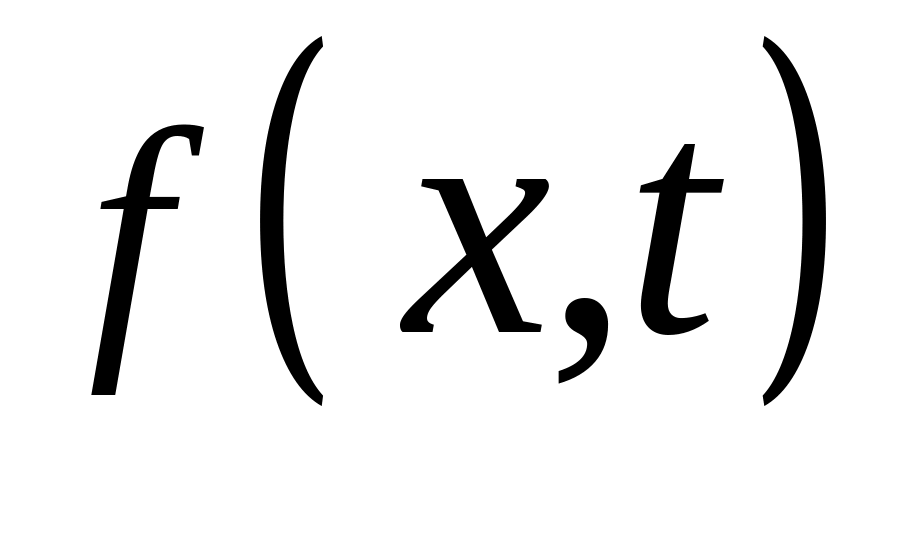в интервале
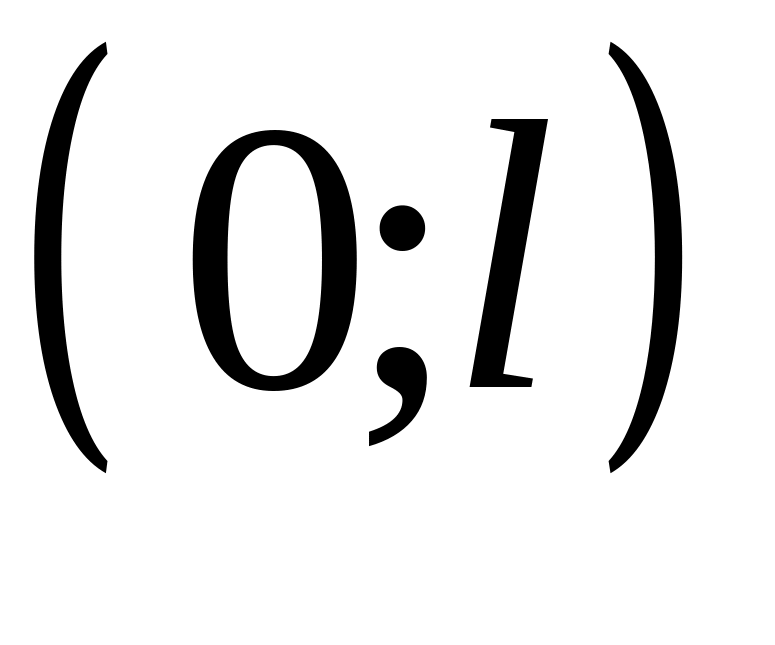в ряд Фурье по синусам (собственным
функциям)
, 
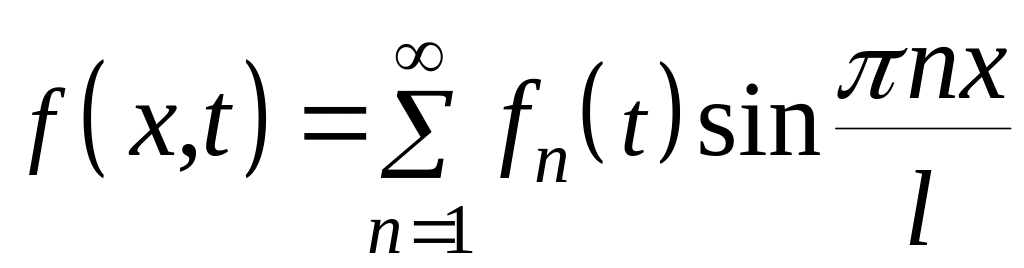где
. 
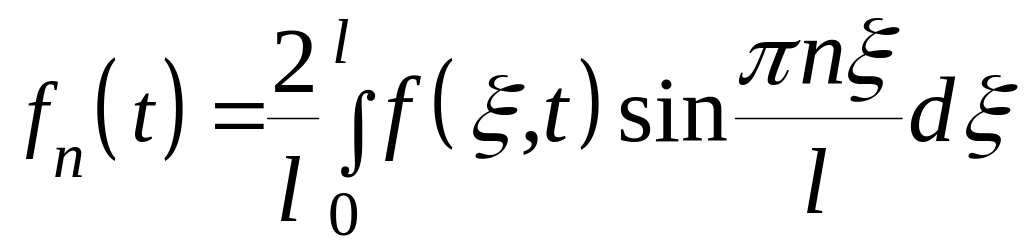Сравнивая разложения и для одной и той же функции , получим дифференциальные уравнения
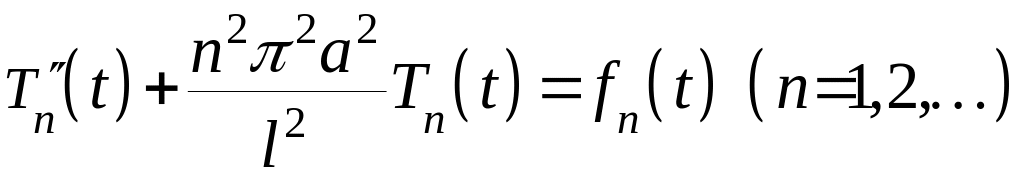
для
неизвестных функций
.
Решения
этого уравнения должны подчиняться
начальным условиям
.
Решаем уравнения и подставляем полученные решения в ряд .
Записываем ответ.
Замечание. В некоторых случаях можно обойтись без разложения функции в ряд Фурье.
Пример 6. Решить смешанную задачу.
Решение.
Собственными функциями однородной краевой задачи являются функции
,
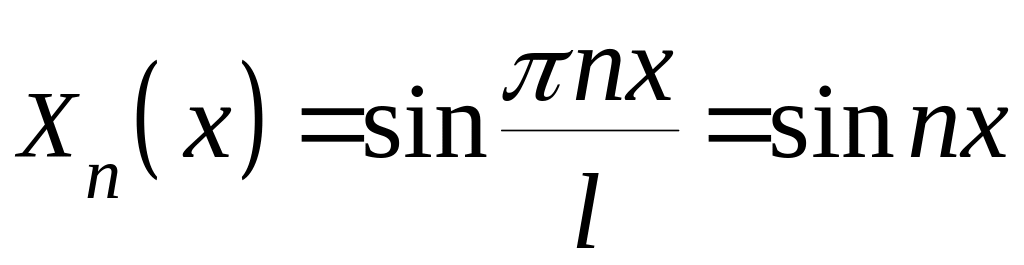поэтому решение ищем в виде
.
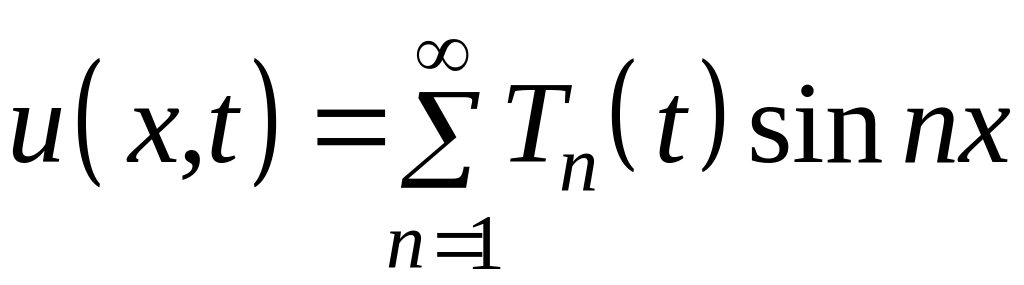Подставим в уравнение, получим
,
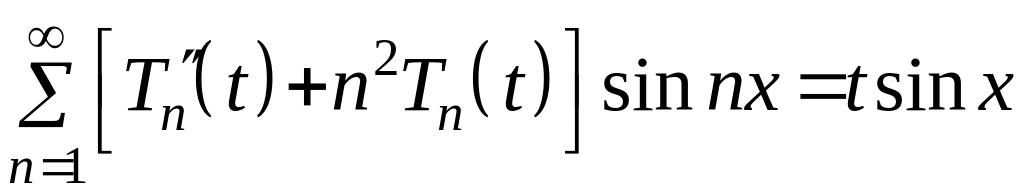откуда легко усматриваем, что
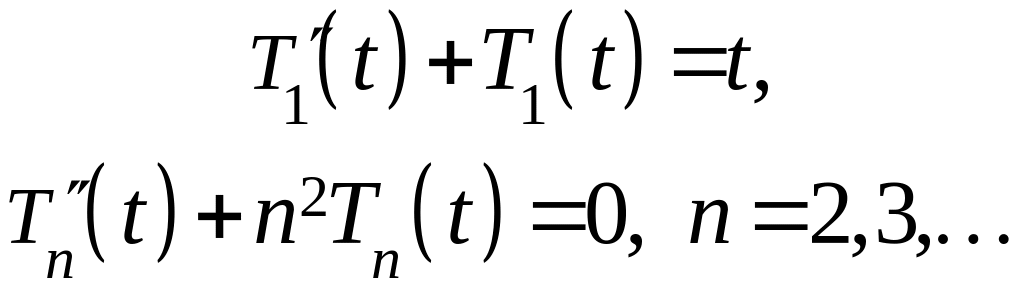
Решения должны удовлетворять начальным условиям
.
Ищем функцию
как решение задачи
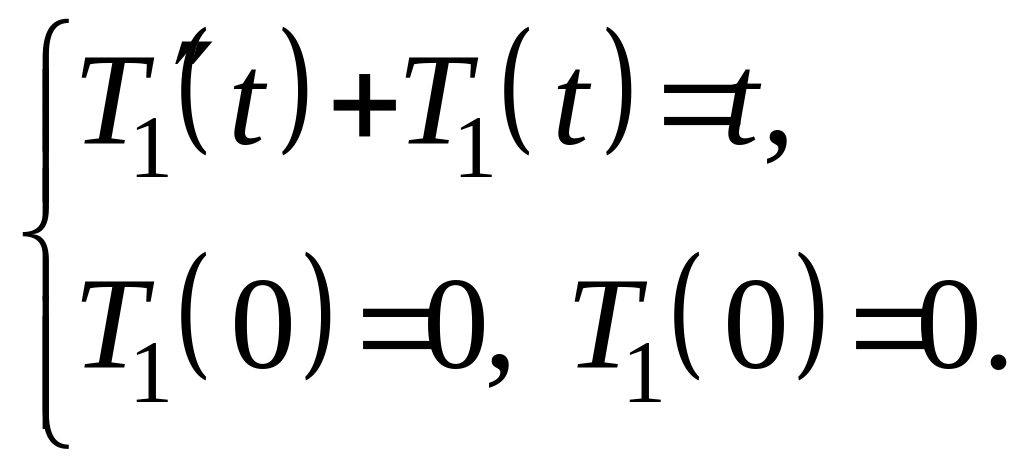
Это
обыкновенное неоднородное линейное
дифференциальное уравнение с постоянными
коэффициентами со специальной правой
частью. Его общее решение
,
где
- общее решение соответствующего
однородного уравнения,
- частное решение неоднородного уравнения.
Найдём
.
Характеристическое уравнение имеет
вид
,
следовательно,
.
Тогда
.
Так
как правая часть уравнения многочлена
1-й степени, то
.
Подставляя
эту функцию в уравнение и сравнивая
коэффициенты при одинаковых степенях
в его левой и правой частях, получим
и
.
Тогда
.
Общее решение неоднородного уравнения имеет вид
.
Потребовав
выполнение начальных условий
,
находим
,
так что
.
Для
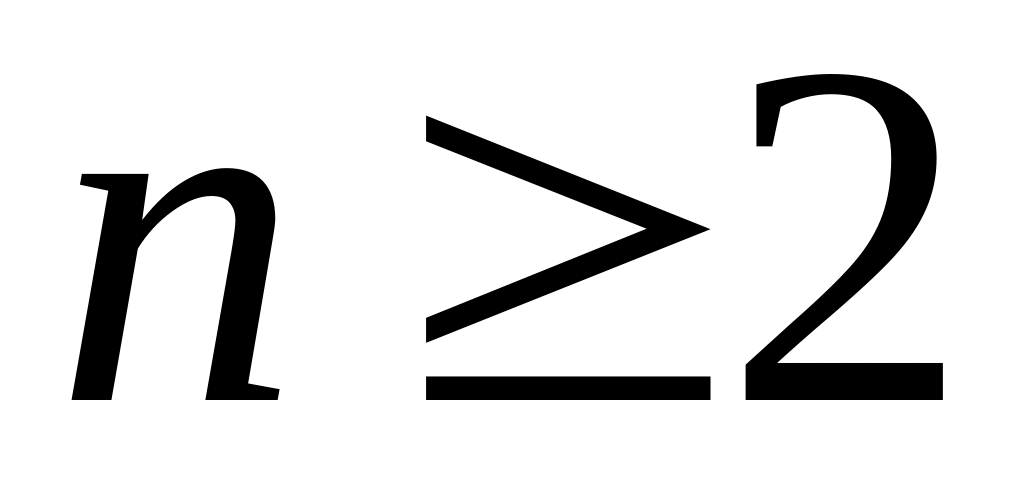имеем
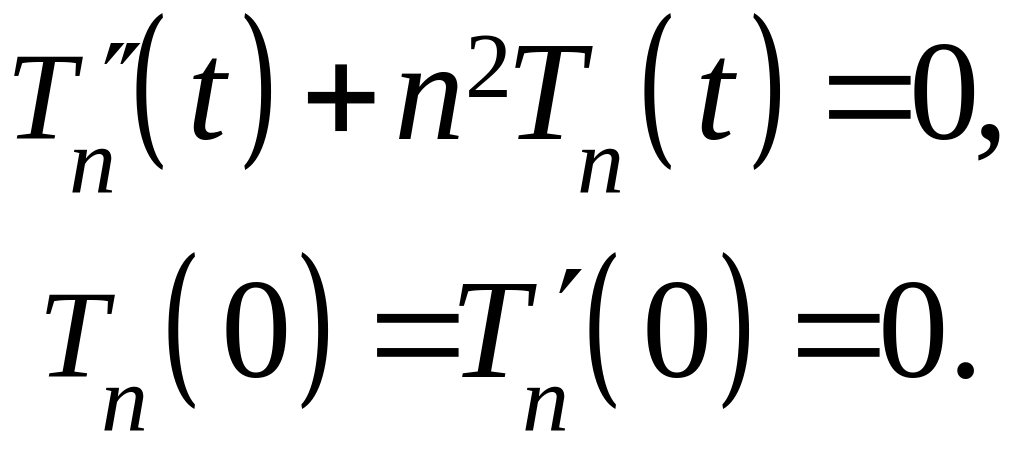
Решая
это линейное однородное дифференциальное
уравнение с постоянными коэффициентами,
получим
.
Решение исходной задачи имеет вид
.