1.5. Построение передаточной функции и характеристического полинома многоконтурной системы управления с использованием формулы Мейсона

Рассмотрим возможность формирования на основе многоконтурного структурного представления системы ХП общего вида с выделенными искомыми коэффициентами стабилизации:

. (1.32)

С этой целью воспользуемся одним из положений теории графов, а именно формулой Мейсона [10, 12], формализующей процедуру получения выражения для ПФ сложной многоконтурной системы:

, (1.33)

где – ПФ отдельных прямых путей от входа к выходу схемы, т.е. от входного воздействия к выходной величине; – полином после изъятия из схемы r–го прямого пути;

, (1.34)

где – сумма ПФ всех контуров схемы; , – суммы произведений двух, трех и т.д. ПФ контуров, не соприкасающихся друг с другом.

Продемонстрируем применение формулы Мейсона на примере схем, приведенных в п.1.1 на рис. 1.4, 1.5.

Обоснуем выражение (1.9) для ПФ параметра стабилизации (от входа к выходу ) замкнутой системы (рис. 1.4). Анализ структуры схемы, приведенной на этом рисунке, выполнен в соответствии с соотношениями (1.33), (1.34) и показывает:

1) между точками входа (приложения регулирующего воздействия ) и выхода (датчика параметра стабилизации ) существует единственный прямой путь, определяемый ПФ:

; (1.35)

2) в схеме нет контуров, не соприкасающихся между собой и с прямым путем. Все четыре имеющихся контура – соприкасающиеся со следующими ПФ:

; ; ;

; (1.36)

3) исходя из (1.33), числитель ПФ строится из выражения:

; (1.37)

4) исходя из (1.34), формируется знаменатель:

. (1.38)

Результирующая ПФ принимает вид, соответствующий соотношению (1.9):

. (1.39)

В качестве другого примера применения формулы Мэйсона сформируем ПФ L₁₁(p) параметра ΔТ (от входа S к выходу T) двухконтурной замкнутой системы (рис. 1.5), тем самым подтвердив корректность выражения (1.10).

Выполним по аналогии (1.35)–(1.39) исследования структурной схемы (рис. 1.5):

1) между точками входа и выхода существует два прямых пути:

; ; (1.40)

2) в схеме имеется 3 замкнутых контура:

; ; . (1.41)

Из них первые два не соприкасаются друг с другом, второй контур не соприкасается с первым путем.

Исходя из (1.33), строим числитель ПФ, а из (1.34) – знаменатель.

В окончательном виде ПФ соответствует соотношению (1.10):

. (1.42)

Обозначим

.

Тогда формула (1.42) перепишется в виде

.

Подчеркнем еще раз, что знаменатели любой ПФ, построенной для одной схемы, будут одинаковыми, независимо от расположения точек входа и выхода, а также прямых путей, их соединяющих. Общий знаменатель для всех ПФ схемы является ХП системы. Его свойства определяются лишь совокупностью и комбинациями замкнутых контуров (1.34). В свою очередь, корни ХП полностью определяют динамические свойства системы. Очевидно, что корни и свойства полинома числителя зависят от путей прохождения сигнала в схеме между точками приложения и выхода.

1.6. Обобщенный подход к глубокому эквивалентированию сложных систем управления

Рассмотрим новый подход к моделированию системы произвольной сложности на основе ее обобщенного графоаналитического представления относительно выделенных для настройки контуров стабилизации. В качестве составляющих элементов такого описания предлагается использовать системные собственные и взаимные ПФ параметров стабилизации (например, в ЭЭС – отклонения частоты напряжения шин генераторов ) в нескольких точках регулирования. Эти ПФ могут быть рассчитаны по исходной системе линеаризованных уравнений или получены экспериментально, как результат идентификации системы.

На рис. 1.16 система произвольной сложности структурно представлена через симметрично связанные собственные и взаимные ПФ параметров стабилизации нескольких (например, двух) выделенных станций относительно точек замыкания каналов стабилизации. При этом функции ( ) являются системными, имеющими общий знаменатель , и учитывают отсутствие регулирования параметров АРВ-СД на выделенных для оптимизации станциях. Относительно каждого канала стабилизации , реализующего в АРВ-СД закон регулирования по отклонению и производной параметра , используется формула

, (1.43)

где – ПФ реального звена дифференцирования в канале стабилизации.

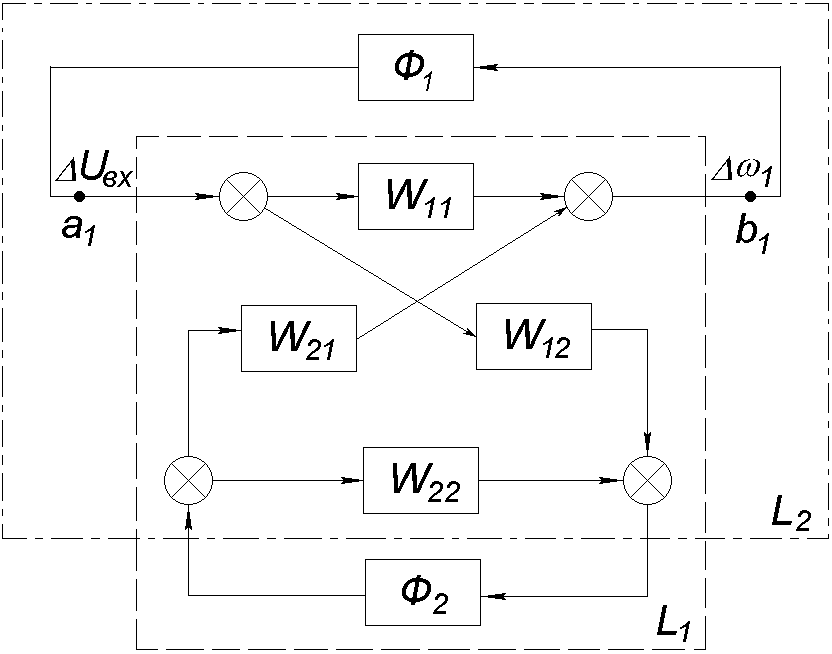
Рис. 1.16. Двухконтурное структурное представление сложной ЭЭС

Оставшаяся часть структурной схемы математически определяется ПФ системы, разомкнутой по данному каналу:

, (1.44)

где – ХП нерегулируемой по _u системы; – полином, полученный из ХО заменой соответствующего столбца на столбец возмущения, подаваемого в точку замыкания канала стабилизации в АРВ-СД.

Характеристический полином регулируемой системы определяется выражением для структуры со звеном обратной связи :

. (1.45)

Граница колебательной устойчивости при и кривые равного качества ( ) могут быть построены путем решения относительно искомых коэффициентов и комплексного уравнения .

Предлагаемое графоаналитическое описание позволяет обобщить структурные представления одной и той же сложной системы при разном количестве выделяемых для оптимизации параметров АРВ-СД станций. Так, например, используя структурную схему системы с тремя выбранными станциями (пусть для определенности две из них были учтены в структурных построениях рис. 1.16), можно получить более подробное выражение для ПФ замкнутой системы того же параметра стабилизации (1.44):

. (1.46)

При этом простота записи достигается использованием найденных выражений для матричных определителей, составленных из собственных и взаимных ПФ:

, , ,

. (1.47)

Заметим, что в (1.46), как и в последующих соотношениях, для сокращения опущен оператор «p».

Подобным же образом может быть записано и общее выражение для ПФ того же параметра стабилизации (L₀₁) при произвольном числе (n) выделенных в системе станций. Из анализа обобщающей формулы Мейсона и соотношений (1.46, 1.47) следует, что при переходе к структурному представлению системы, учитывающему большее на единицу число точек регулирования, необходимо раскрыть структуру каждого элемента исходного графа. Например, для случая с двумя и тремя выделенными станциями указанная связь определяется более подробным описанием собственных и взаимных ПФ W_ij, соответствующих двухточечной структуре (рис. 1.16), через аналогичные , уже относительно трех выделенных каналов стабилизации:

(1.48)

Из (1.48) следует, что развертывание структуры происходит за счет введения явного описания ПФ третьей станции. Поскольку развертывание и сворачивание структуры проводится с использованием общего выражения, т.е. независимо от количества контролируемых контуров, определим найденное свойство как рекуррентность структурного представления.

На основании формулы Мейсона и общего ряда контуров по заданным ПФ, а именно

, , , (1.49)

может быть записан искомый ХП D(p) с явно выделенными в нем n-парами коэффициентов стабилизации k_0i, k_1i (i= 1,n):

. (1.50)

При этом искусственно введенные для упрощения записи взаимные симметричные функции , … формируются минорами, составленными из операторного определителя:

, (1.51)

где i = 1,n.

Подчеркнем, что восстановленный на основе формальных функций ХП D(p) содержит в виде слагаемых полином с фиксированными коэффициентами , отражающий свойства нерегулируемой части системы, и полиномы, коэффициенты которых являются либо функцией параметров только одного канала стабилизации , либо функцией произведения каналов ( ).

Отметим, что собственные и взаимные характеристики разомкнутой системы , используемые для формирования многопараметрического полинома с целью координации настроечных параметров АРВ-СД, могут быть получены по аналогии с рассмотренным выше способом (1.26), (1.27), т.е. путем обработки результатов эксперимента по получению собственных и взаимных ЧХ (L_0ij) параметра стабилизации замкнутой по всем контурам системы [9].