1.4. Методы построения эквивалентных пф для упрощенного моделирования многосвязных систем управления

Как следует из п.1.1 (рис. 1.5) и п. 1.2 (рис. 1.11), любую многоконтурную многосвязную систему можно строго представить в виде одноконтурной.

Для того чтобы управлять системой с помощью такой модели, необходимо иметь эквивалентную ПФ системы , разомкнутой по выделенному контуру регулирования (рис. 1.13).

Рис. 1.13. Одноконтурное представление многосвязной, разомкнутой по каналу регулирования системы с использованием эквивалентной ПФ

Эквивалентную ПФ можно определить тремя методами:

– с использованием полной модели в виде системы ДУ, если она имеется;

– путем идентификации (построение аналитической модели по данным экспериментальных наблюдений);

– с использованием формулы Мейсона [10, 12], по математическому описанию структурно входящих в ПФ элементарных звеньев, элементов и подсистем, если оно известно.

Напомним, что первый метод подробно изложен в предыдущем разделе (п. 1.3) и заключается в использовании фундаментальной матрицы замкнутой системы для построения главного определителя и его минора , формируемого вычеркиванием строки и столбца, соответствующих входной и выходной переменной. Окончательно имеем:

. (1.22)

Поясним особенности второго пути. Они связаны с использованием для синтеза эквивалентной аналитической модели в виде ПФ экспериментальных амплитудно-фазовых частотных характеристик (АФЧХ).

Известно, что по заданной ПФ заменой операторов ( ) может быть получена выборка комплексных чисел , представляющая соответствующую АФЧХ выходной переменной относительно входной (например, для схемы на рис. 1.13 и ). В результате идентификации должна быть решена обратная задача – по экспериментально определенной АФЧХ ( ) найдена эквивалентная ПФ .

Существуют методы идентификации, позволяющие определять АФЧХ системы между любой парой точек входа и выхода при наличии соответствующих временных выборок сигнала и (рис. 1.14). В их основе лежит использование соотношения связи переменных во временной области в виде интеграла Дюамеля (свертки) входной выборки и весовой функции системы (1.23). При этом если известна функция , то установлена однозначная связь между отсчетами входного и выходного сигналов, т.е. известна модель системы в непараметрическом виде (в виде временной выборки) [12]:

. (1.23)

Свертка выборок во временной области соответствует произведению комплексных изображений этих выборок в частотном спектре (1.24):

. (1.24)

Рис. 1.14. Моделирование системы с использованием весовой функции

Из (1.24) следует, что АФЧХ является частотным изображением весовой функции и может быть определена отношением спектров выходного и входного сигналов (1.25), которые, в свою очередь, могут быть получены путем преобразования Фурье временных выборок реальных сигналов:

. (1.25)

Заметим, что изложенная схема метода определения АФЧХ по выборкам реальных сигналов на практике применима лишь к замкнутым системам, функционирующим с рабочими настройками регуляторов, поскольку размыкание системы для проведения эксперимента недопустимо по соображениям нарушения нормальных условий эксплуатации и даже потери устойчивости. Данные трудности легко преодолимы, если использованы известные прямое и обратное соотношения связи между функциями замкнутой и разомкнутой одноконтурной системы при известном математическом описании и рабочих настройках регулятора . В частности, для схемы на рис. 1.13 такими соотношениями для частотных характеристик (ЧХ) будут являться выражения (1.26, 1.27):

; (1.26)

. (1.27)

По первому из них может быть рассчитана независимая от настроек характеристика разомкнутой системы при известных характеристиках замкнутой системы и регулятора . Второе выражение, при наличии уже известной характеристики разомкнутой системы , используется для выбора новых настроечных параметров того же регулятора Ф₂, из условия обеспечения желаемых динамических свойств новой замкнутой системы .

Таким образом, результатом непараметрической идентификации является искомая АФЧХ разомкнутой системы. Для проведения этапа параметрической идентификации её необходимо представить в виде двух действительных выборок: амплитудной частотной характеристики (АЧХ) и фазовой частотной характеристики (ФЧХ) (рис. 1.15).

ω

Рис. 1.15. Примерный вид АЧХ и ФЧХ, эквивалентирующих сложную систему моделью второго дифференциального порядка

Опыт исследований показывает [9], что АЧХ и ФЧХ, полученные расчетным путем, при использовании полной математической модели в виде фундаментальной матрицы или путем обработки экспериментальных данных, независимо от сложности системы имеют конфигурацию, соответствующую ПФ невысокого (не более 5) порядка, что объясняется явлением компенсации равных или близких по значению полюсов (корней полинома знаменателя) и нулей (корней полинома числителя соответствующей ПФ (1.21). Это облегчает задачу параметрической идентификации системы в виде несложной ПФ – выявления нескольких «оставшихся» нескомпенсированных корней знаменателя и числителя. В частности, АЧХ и ФЧХ, приведенные на рис. 1.15, эквивалентируют систему моделью второго дифференциального порядка. Здесь графики определяются свойствами одной пары комплексно-сопряженных корней, расположенной в знаменателе эквивалентной ПФ:

. (1.28)

При анализе колебательной устойчивости наибольший интерес представляют составляющие, которые соответствуют комплексным нулям и полюсам ПФ. Так, АЧХ и ФЧХ для i-й комплексно-сопряженной пары корней имеют вид

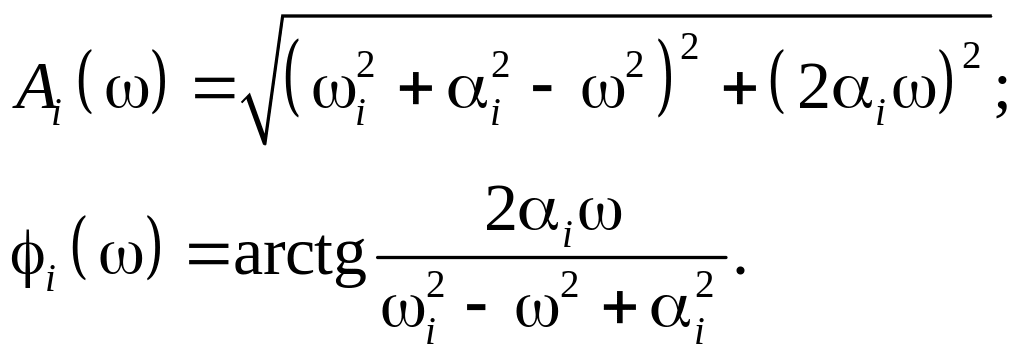(1.29)

Из соотношений (1.29) следует:

1. Амплитудно-частотная зависимость комплексной пары полюсов имеет максимум (/минимум) при частоте

. (1.30)

При этом амплитуда пропорциональна вещественной части корня: .

2. Фазовая характеристика при изменении от 0 до ∞ получает приращение . Скорость приращения зависит от величины . При производная зависимости имеет наибольшую величину, которая связана с соотношением

. (1.31)

3. Направление изменения годографа зависит от знака вещественной части корня. Приращение фазы совпадает с её знаком.

В силу отмеченного первого свойства, минимумы и максимумы характеристики позволяют локализовать частоты, отвечающие нулям и полюсам с минимальными вещественными частями. В свою очередь, известно, что годограф суммарной ФЧХ на выделенных частотах при одинаковых, например отрицательных, знаках вещественных частей нулей и полюсов имеет положительное приращение для первых и отрицательное для вторых. Кроме того, весьма важным для идентификации вещественных частей полюсов и нулей является соотношение (1.31), формализующее резонансное свойство ФЧХ. Его можно сформулировать следующим образом: величина вещественной части нуля или полюса на резонансной частоте (1.30) обратно пропорциональна скорости изменения фазы. Тем самым возможна количественная оценка отдельных нулей и полюсов.

Таким образом, этап параметрической идентификации системы в виде несложной ПФ сводится к последовательному выявлению действительных и мнимых частей доминирующих (нескомпенсированных) корней числителя и знаменателя. На практике он состоит в выполнении в соответствии с табл. 1.1 качественного анализа конфигурации АЧХ и ФЧХ, где в разной степени проявляются резонансные свойства различных нулей и полюсов.

Тем самым подробно раскрыта схема второго метода построения эквивалентной ПФ многосвязной системы – путем идентификации.

Таблица 1.1

Формализация частотных свойств нулей и полюсов, определяющих структуру и количественные характеристики предполагаемой ПФ

Тип корня	Формализация частотных свойств корня
Комплексный полюс	Имеет резонансный амплитудный пик и наиболее интенсивное изменение фазы на частоте среза. Знак изменения фазы определяется знаком действительной части полюса (для устойчивого звена – отрицательный). Суммарное изменение фазы стремится к величине 180
Действительный полюс	Имеет падающую АЧХ с максимумом на нулевой частоте и суммарное изменение фазы на 90 во всем частотном диапазоне. Знак изменения фазы совпадает со знаком полюса
Комплексный нуль	Имеет амплитудный минимум и наиболее интенсивное изменение фазы на частоте среза. Знак изменения фазы определяется знаком действительной части полюса (для устойчивого – положительный). Суммарное изменение фазы стремится к величине 180
Действительный нуль	Имеет монотонно возрастающую амплитудную характеристику и суммарное изменение фазы на 90 во всем частотном диапазоне. Знак изменения фазы противоположен знаку нуля
Нуль, полюс	Величина вещественной части на резонансной частоте обратно пропорциональна скорости изменения фазы

Основные положения и особенности последнего, третьего метода формирования ПФ на основе математического описания входящих в структуру системы элементарных звеньев, элементов и подсистем, ввиду самостоятельной значимости материала, изложены в следующем разделе (п. 1.5).