3.3.9. Определение оптимальных настроечных коэффициентов арв-сд

Задача поиска экстремума функции означает нахождение её максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области её аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум. Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют ещё задачами оптимизации.

При отыскании оптимальных настроечных параметров регулятора в качестве целевой функции примем степень устойчивости . Представим как функцию двух аргументов – настроечных параметров регулятора :

. (3.140)

Поскольку при решении поставленной задачи оптимизации необходимо отыскать наименьшее значение степени устойчивости системы, то справедлива запись

. (3.141)

Из конфигурации кривой Д-разбиения (рис. 3.15) с помощью булевых операторов запишем логические выражения, задающие ограничения на значения аргументов минимизируемой функции:

(3.142)

Ограничение установлено исходя из технических характеристик регуляторов возбуждения, поскольку настроечные коэффициенты усиления АРВ-СД по отклонению и производной частоты напряжения статора не могут превышать 10 делений.

В качестве начального приближения выберем точку, лежащую за пределами кривой Д-разбиения, а именно: дел., дел. (рис. 3.15).

Программой, реализующей градиентный метод, были найдены следующие оптимальные настроечные коэффициенты регулятора: дел., дел.

В табл. 3.5 записаны собственные значения ХП замкнутой системы (3.109), полученные при новых настройках АРВ-СД.

Таблица 3.5

Собственные значения характеристической матрицы

Затухание, с–1	Частота, Гц
-0,163	5,37
-0,163

Как видно из данных табл. 3.5 вещественная часть комплексно-сопряжённого корня и вещественный корень равны между собой, то есть при найденных оптимальных настройках регулятора колебательная и апериодическая составляющие собственного движения системы находятся в равновесии. Отметим полученные значения корней на комплексной плоскости (рис. 3.16).

Рис. 3.16. Расположение корней ХП на комплексной плоскости

На рис. 3.17, 3.18 представлены ЧХ, соответствующие найденным настроечным параметрам АРВ-СД. Из рис. 3.17 видно уменьшение значения амплитуды на резонансной частоте почти в 2,5 раза по сравнению с АЧХ разомкнутой системы при неизменности самой частоты (рис. 3.7). Последний факт говорит об улучшении качества ПП.

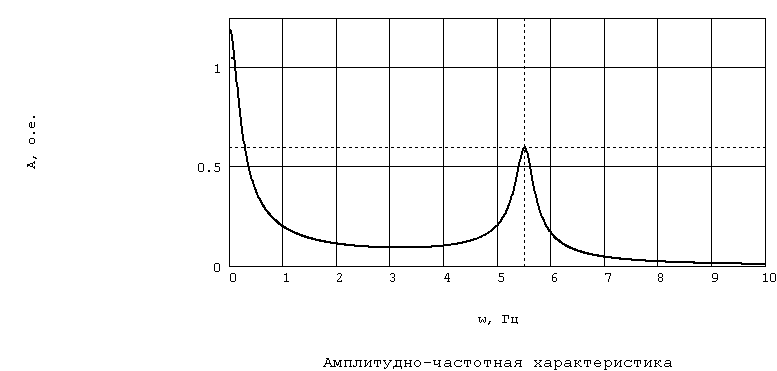
Рис. 3.17. АЧХ замкнутой системы

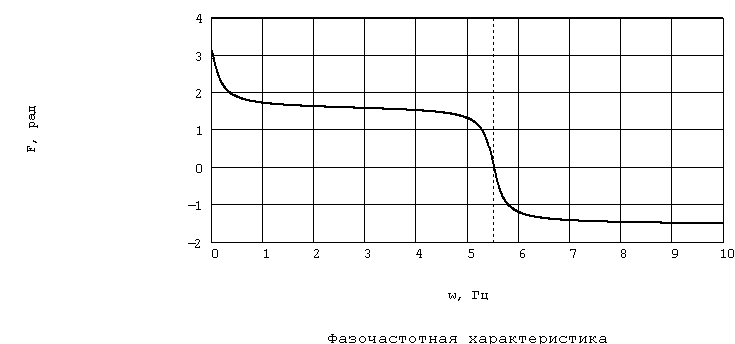
Рис. 3.18. ФЧХ замкнутой системы

На основании вышеизложенного материала можно заключить следующее. Алгоритм нахождения оптимальных настроек АРВ-СД включает два этапа. Первый этап состоит в построении границы устойчивости (Д-разбиения) и отыскании рациональных настроек АРВ-СД, обеспечивающих общую устойчивость исследуемой системы. Второй этап характеризуется поиском условного экстремума целевой функции ( ) и нахождением оптимальных настроечных коэффициентов регулятора. Формальным признаком этого может служить равенство действительного корня и вещественной части комплексного корня (рис. 3.16). Новые коэффициенты обеспечивают наилучшие динамические свойства простейшей ЭС (рис. 3.17, 3.18).